순환(Recursion)이란?
알고리즘이나 함수가 수행중 다시 자기 자신을 호출하여 문제를 해결하는 것
정의 자체가 순환적으로 되어 있는 경우에 적합함
📕 순환 호출의 내부 구현
프로그래밍 언어에서 하나의 함수가 자기 자신을 호출하는 것과 다른 함수를 호출하는 것은 동일함
- 복귀 주소: 시스템 스택에 저장
- 호출되는 함수를 위한 매개변수, 지역 변수: 스택으로부터 할당 받음
- 시스템 스택에서의 공간 = 활성 레코드(activation record)
- 순환호출이 중첩될 수록 시스템 스택에는 활성 레코드들이 쌓이게 됨
int factorial(int n){
if(n<=1) return 1;
else return n*factorial(n-1);
}* factorial(3) 호출 중 시스템 스택 변화
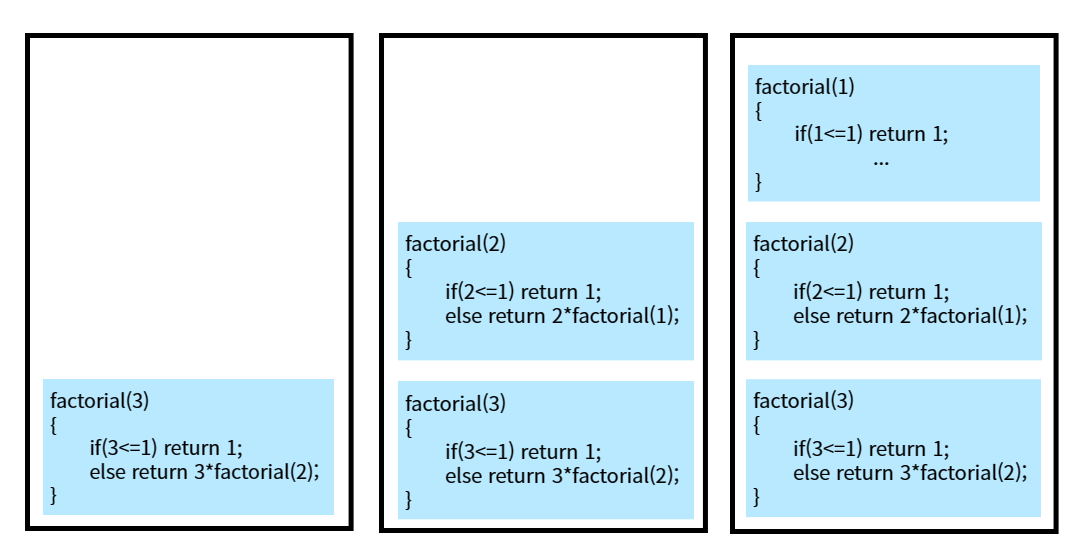
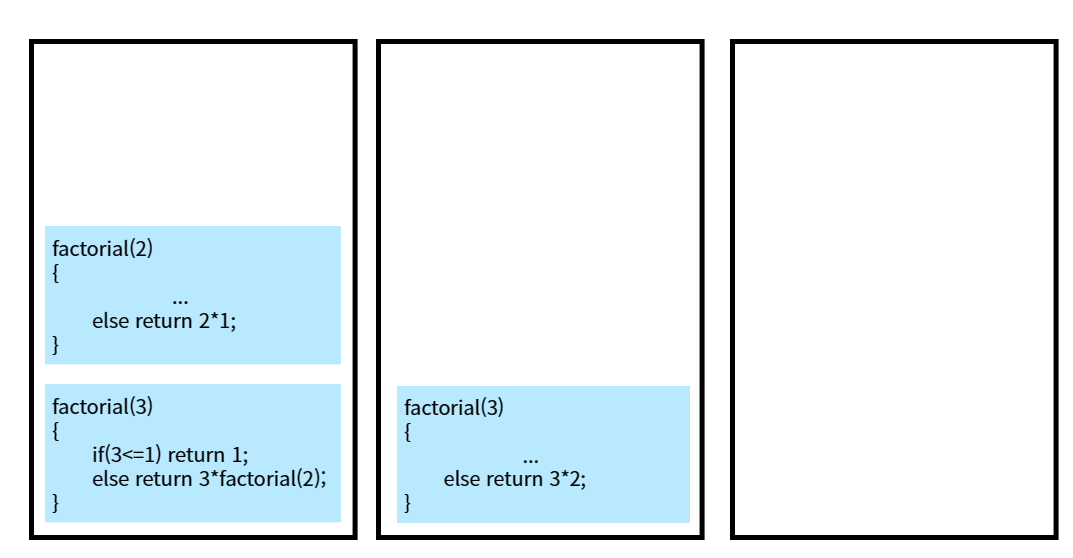
호출된 함수가 끝나게 되면 시스템 스택에서 복귀주소를 추출하여 호출한 함수로 되돌아 감(할 일 끝나면 집으로 다시 온다.)
📒 순환 알고리즘 구조
a. 순환을 멈추는 부분 (종료)
b. 순환을 호출하는 부분 (패턴)
종료가 없다면 시스템 스택을 모두 사용할 때까지 호출되다가 오류를 내며 멈출 것이다.
// 종료 부분이 없는 factorial 함수
int factorial(int n)
return n*factorial(n-1);팩토리얼 함수는 무한히 순환 호출을 하게 되고, 오류를 발생시킨다.
따라서 순환 호출에는 순환 호출을 멈추는 문장이 반드시 포함 되어야 한다.
📖 순환 vs 반복
- 순환은 문제의 정의가 순환적으로 되어있는 경우 작성하기가 훨씬 쉽다.
- 순환 형태의 코드가 가독성이 증대되고 코딩도 간단하다.
* 순환은 반복에 비해 수행속도가 낮다.
// 팩토리얼 순환 ver.
int factorial(int n){
if(n<=1) return 1;
else return n*factorial(n-1);
}
// 팩토리얼 반복 ver.
int factorial(int n){
int result =1;
for(int i =2;i<=n;i++)
result *=i;
return result;
}위 두 함수의 시간복잡도는 O(n)으로 동일
순환 호출의 경우 여분의 기억공간이 더 필요하고 함수를 호출하기 위해서는 함수의 매개변수들을 스택에 저장하는 것과 같은 사적 작업이 필요하다.
-> 수행시간이 더 많이 걸림
📗 문제를 통한 순환, 반복 비교
ex) 거듭제곱값 계산
숫자 x의 n 거듭제곱 값인 X^n을 구하는 문제
순환적인 방법이 더 효율적인 문제
// 반복적인 방법
double slow_power(double x, int n){
double result = 1.0;
for(int i=0;i<n;i++)
result*=x;
return result;
}
// 순환적인 방법
double power(double x, int n){
if(n==0) return 1;
else if(n%2==0)
return power(x*x, n/2);
else return x*power(x*x, (n-1)/2)
}순환적인 방법:
xⁿ=(x²)^n/2의 공식을 이용하여
n이 짝수인 경우 x²을 먼저 계산한 후 이 값은 n/2제곱함.
n이 홀수인 경우 x²를(n-1)/2 제곱하고 여기에 x를 곱함
한 번의 순환 호출을 할 때마다 문제의 크기는 약 절반으로 줄어든다.
ex) 100 -> 50 -> 25 -> 12 -> 6 -> 3 -> 1
따라서 거듭제곱값을 계산하는 경우 순환호출을 이용하는 게 훨씬 효율적이다.
📖 시간복잡도 비교
- 순환적인 방법: O(logN)
- 반복적인 방법: O(N)

