[프로그래머스 Level.2] 퍼즐 게임 챌린지 - 이진탐색

알고리즘 유형 : 이진 탐색
풀이 없이 스스로 풀었나요? : ⭕

---

문제 - 퍼즐 게임 챌린지

소스코드

/**
 * 프로그래머스 Level2 퍼즐 게임 챌린저 - 이진 탐색
 * https://school.programmers.co.kr/learn/courses/30/lessons/340212?language=java
 */
class Solution {

    // 주어진 숙련도에 따른 총 소요 시간을 계산하는 메서드
    public long calcTotalTime(int[] diffs, int[] times, int curLevel) {
        long totalTime = times[0]; // 첫 번째 문제는 무조건 풀 수 있으므로 초기 값을 설정

        // 두 번째 문제부터 마지막 문제까지 반복
        for (int i = 1; i < diffs.length; i++) {
            int curDiff = diffs[i]; // 현재 문제의 난이도
            int curTime = times[i]; // 현재 문제를 푸는 데 걸리는 시간
            int prevTime = times[i - 1]; // 이전 문제를 푸는 데 걸린 시간

            // 현재 난이도가 현재 숙련도 이하라면 바로 문제를 풀 수 있음
            if (curDiff <= curLevel) {
                totalTime += curTime;
            } 
            // 현재 난이도가 현재 숙련도보다 크면 이전 문제로 돌아가야 함
            else {
                int cnt = curDiff - curLevel; // 차이만큼 추가 학습 필요
                totalTime += (prevTime + curTime) * cnt + curTime;
            }
        }

        return totalTime; // 총 소요 시간을 반환
    }

    // 이분 탐색을 통해 적정한 레벨을 찾는 메서드
    public int solution(int[] diffs, int[] times, long limit) {
        int lt = 1; // 최소 숙련도
        int rt = 100000; // 최대 숙련도

        // 이분 탐색을 통해 조건에 맞는 숙련도를 찾음
        while (lt < rt) {
            int mid = (lt + rt) / 2; // 중간을 계산

            // 현재 숙련도에서 계산한 총 시간이 제한 시간보다 크면 레벨을 더 높여야 함
            if (limit < calcTotalTime(diffs, times, mid)) {
                lt = mid + 1; // 숙련도를 올림
            } 
            // 제한 시간 내에 풀 수 있으면 레벨을 줄여가며 최소한의 레벨을 찾음
            else {
                rt = mid; // 숙련도를 낮춤
            }
        }

        return rt; // 조건에 맞는 숙련도 반환
    }
}

후기

문제를 보고 이진 탐색이 떠올라 풀긴 했지만 경계 설정하는데 애를 먹었다.
어느 조건에 =을 넣어줘야 하며 lt, rt 갱신 시 mid로 할지 mid -1 혹은 mid + 1로 할지 어려움을 느껴 정리해볼려고 합니다.

1차 시도 (실패)

		int lt = 1; // 최소 숙련도
        int rt = 100000; // 최대 숙련도


        while (lt < rt) {
            int mid = (lt + rt) / 2;

            if (limit < calcTotalTime(diffs, times, mid)) {
                lt = mid;
            } 
            else {
                rt = mid; 
            }
        }

😭 left = mid 는 사용하면 안 된다.

조건에 따라 될 수도 있겠지만 위 조건에서 left = mid를 사용하면 left, right 사이에 두 원소만 남았을 때 left가 움직이지 못 하므로 무한루프에 빠진다.

✨ mid 계산 시 정수로 내림하기 때문에 주의해야 할 점이다.

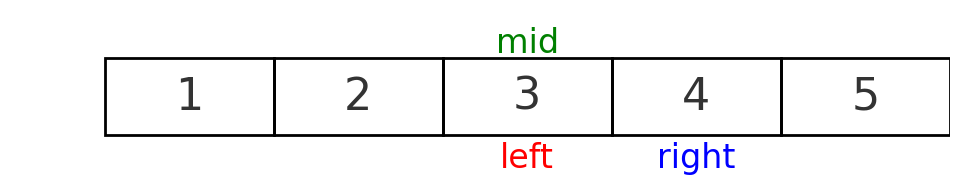
예시

• 배열 상태: [1, 2, 3, 4, 5]
• left: 3, right: 4
• target : 4
• mid 계산: (3 + 4) // 2 = 3 → mid 값은 3
• 비교: 3 < 4 → 다시 left = mid로 설정하려고 하면 left가 움직이지 않고 3에서 멈춤
  

1차 시도 (수정)

		int lt = 1; // 최소 숙련도
        int rt = 100000; // 최대 숙련도


        while (lt < rt) {
            int mid = (lt + rt) / 2;

            if (limit < calcTotalTime(diffs, times, mid)) {
                lt = mid + 1;
            } 
            else {
                rt = mid; 
            }
        }

🤔 left = mid는 안 되는데 right = mid는 왜 되는가?

mid 계산 특성 (정수 내림) 때문이다.
두 원소만 남은 경우 mid는 left랑 같고 조건식을 만족하면 left가 right로 이동하고 조건식을 만족하지 않으면 right가 mid(이 경우에는 left랑 같음)로 이동하므로 left == right여서 반복문을 빠져나온다.

2차 시도 (실패)

		int lt = 1; // 최소 숙련도
        int rt = 100000; // 최대 숙련도


        while (lt <= rt) {
            int mid = (lt + rt) / 2;

            if (limit < calcTotalTime(diffs, times, mid)) {
                lt = mid + 1;
            } 
            else {
                rt = mid; 
            }
        }
        
        return rt;

right = mid를 사용할 경우 left == right, arr[mid] == target 일 때 반복문을 못 빠져나오는 경우가 생긴다. 그래서 while 조건에서 등호가 포함되어 있을 경우 right = mid - 1을 사용한다.

2차 시도 (수정)

		int lt = 1; // 최소 숙련도
        int rt = 100000; // 최대 숙련도


        while (lt <= rt) {
            int mid = (lt + rt) / 2;

            if (limit < calcTotalTime(diffs, times, mid)) {
                lt = mid;
            } 
            else {
                rt = mid - 1; 
            }
        }
        
        return lt;

---