[백준 2103 파이썬] 직교다각형 복원 (실버3, 기하학)

알고리즘 유형 : 기하학
풀이 없이 스스로 풀었나요? : ⭕

---

백준 2203번 직교다각형 복원

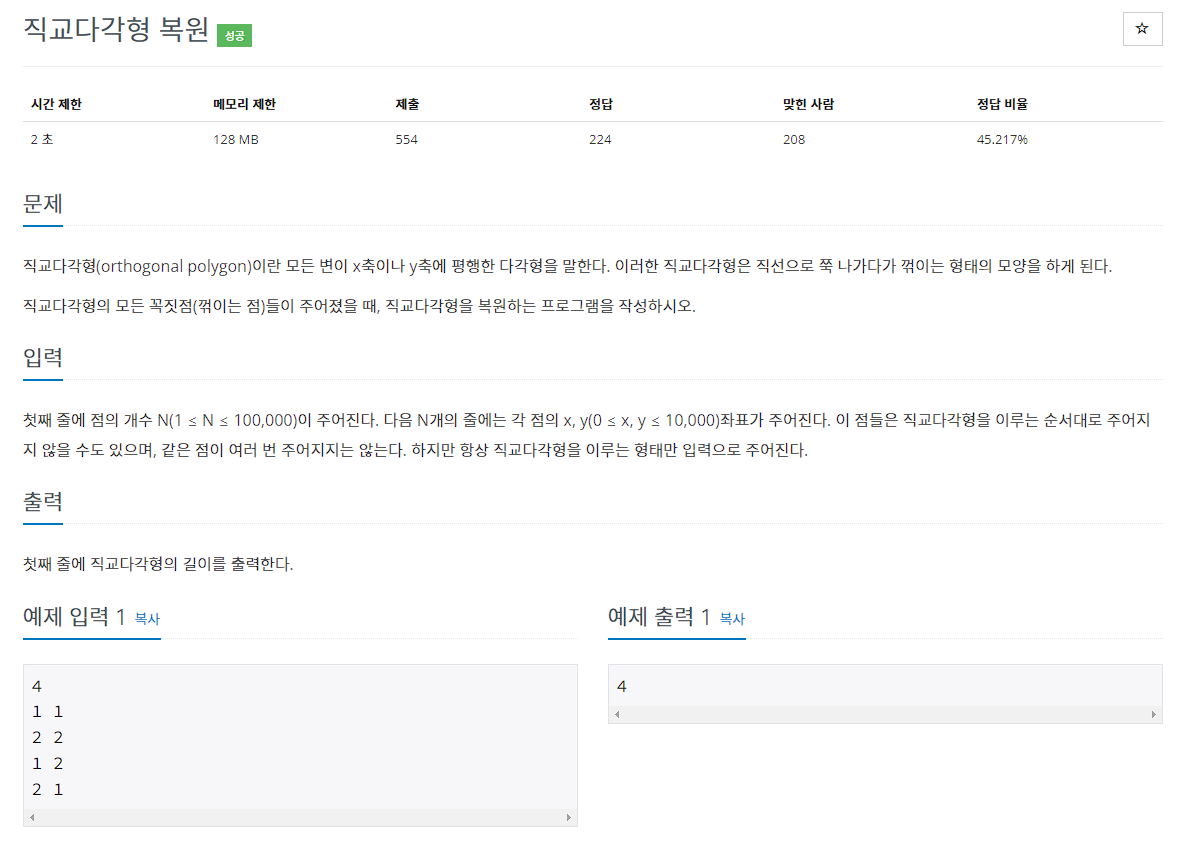
솔루션

예를 들어 다음과 같은 직교다각형이 있다고 하자.

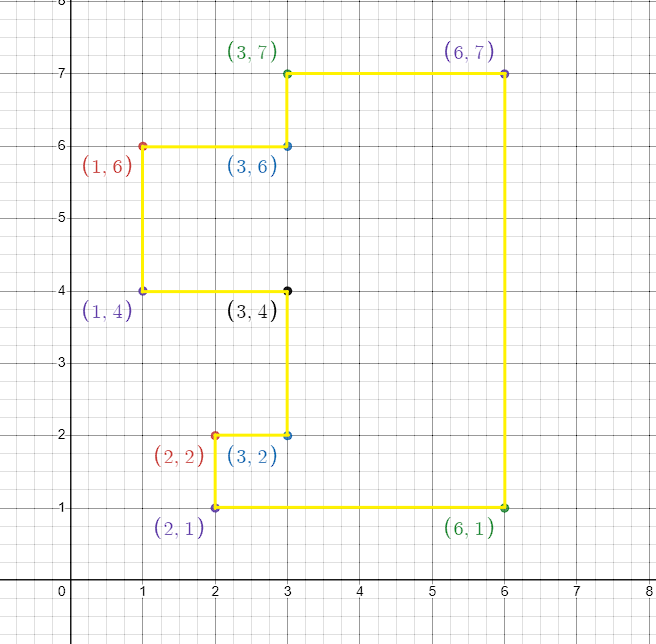
직교 다각형은 x, y축과 평행한 변들로 이루어진 다각형을 의미합니다. 이러한 다각형은 각 변들이 수직 또는 수평 방향을 가집니다.
주어진 직교 다각형의 좌표를 통해 각 변들의 길이를 구하는 방법은 다음과 같습니다.

1. 좌표를 x, y축으로 분리하기

주어진 직교 다각형의 좌표를 x좌표와 y좌표로 분리합니다.

# x 좌표 : [y 좌표] 
{2: [1, 2], 3: [2, 4, 6, 7], 6: [1, 7], 1: [4, 6]}

# y 좌표 : [x 좌표]
{1: [2, 6], 2: [2, 3], 4: [1, 3], 6: [1, 3], 7: [3, 6]}

2. 각 변들의 길이 계산

정렬 후 각 좌표별로 리스트에서 인접한 두 값들을 뺄셈하여 각 변들의 길이를 계산합니다.

예를 들어, x 좌표가 2일 때, 대응하는 y 좌표들은 [1, 2]입니다. 이때 인접한 두 y 좌표의 차이를 구하여 첫 번째 변의 길이를 구합니다. (2 - 1) = 1
마찬가지로, x 좌표가 3일 때 대응하는 y 좌표들은 [2, 4, 6, 7]이며, 인접한 두 y 좌표의 차이를 구하여 두 번째 변의 길이를 구합니다. (7 - 2) = 5
위와 같이 x 좌표에 대응하는 y 좌표들의 차이를 계산하여 모든 변의 길이를 구합니다.

소스 코드

import sys

input = sys.stdin.readline

if __name__ == "__main__":
    n = int(input())
    nums = [tuple(map(int, input().split())) for _ in range(n)]

	# x y별로 분리할 dict 초기화
    grouped_data_x = {}
    grouped_data_y = {}

	# dict에 데이터 삽입
    for x, y in nums:
        grouped_data_x.setdefault(x, []).append(y)
        grouped_data_y.setdefault(y, []).append(x)

	# 최종 길이를 반환할 결과값 초기화
    res = 0

	# dict에서 values값을 가져와 for문 실행
    for x_coords in grouped_data_x.values():
        x_coords.sort() # 정렬하지 않으면 음수 값이 나올 수 있음 ex [1,2]
        for i in range(len(x_coords) - 1, 0, -2): # 인접한 쌍으로 길이 계산 후 추가
            res += x_coords[i] - x_coords[i - 1]

	# dict에서 values값을 가져와 for문 실행
    for y_coords in grouped_data_y.values():
        y_coords.sort() # 정렬하지 않으면 음수 값이 나올 수 있음 ex [1,2]
        for i in range(len(y_coords) - 1, 0, -2): # 인접한 쌍으로 길이 계산 후 추가
            res += y_coords[i] - y_coords[i - 1]

	# 결과값 출력
    print(res)

---

후기

직교다각형이라는 용어가 생소하여 문제에 접근하기 어려웠으나 직접 그려보고 계산하는 과정을 거치니 쉽게 풀 수 있었다.