1. 분할 정복
문제 해결 방법 중에서
가장 유명한 재귀적 기술인
분할 정복 dividid and conquer 전략!
분할 정복 전략은 문제에 바로 적용할 수 있는 단순한 알고리즘이 아니다.
문제를 풀기 위한 방법론에 가깝다.
문제를 분할 정복 전략으로 풀기 위해서는 다음의 두 가지 단계를 거쳐야 한다.
-
기본 단계를 해결한다.
이 부분은 가능한 한 간단한 문제이어야만 한다. -
문제가 기본 단계가 될 때 까지 나누거나 작게 만든다.
2. 퀵 정렬
선택 정렬보다 훨씬 빠르고,
실제로 자주 사용되는 정렬 알고리즘이다.
예를 들면,
C언어에는 qsort라는 함수가 있는데, 바로 퀵 정렬을 구현한 함수이다.
퀵 정렬도 마찬가지로 분할 정복 전략으로 만들어진 알고리즘이다.
배열을 정렬 해본다고 가정해보면,
우선
정렬하는데 가장 간단한 배열은
" 비어있는 배열 " , " 원소가 하나인 배열 " 이다.
이러한 비어있는 배열이나, 원소가 하나인 배열이 기본 단계가 된다.
이때는 배열을 있는 그대로 반환하면 된다.
배열이 긴 경우,
배열을 기본 단계가 될 때까지 나누면 된다.
퀵 정렬의 동작은 다음과 같다.
1 . 배열에서 원소를 아무거나 하나 고른다.
이 원소가 기준 원소 pivot 가 됨.
2 . 모든 원소를 기준 원소보다 작은 원소와 큰 원소로 분류한다.
이것을 분할 partitioning 이라고 한다.
이제 배열은
기준 원소보다 작은 숫자로 이루어진 하위 배열,
기준 원소 ,
기준 원소보다 큰 숫자들로 이루어진 하위 배열로 구성되었다.
하위 배열들은 정렬되어있지 않기 때문에,
각각의 하위 배열에 대해서도 퀵 정렬을 호출한 후
결과를 합친다.
java 코드 구현
배열을 새로 만들지 않고,
포인터를 사용해서 배열의 크기를 지정.
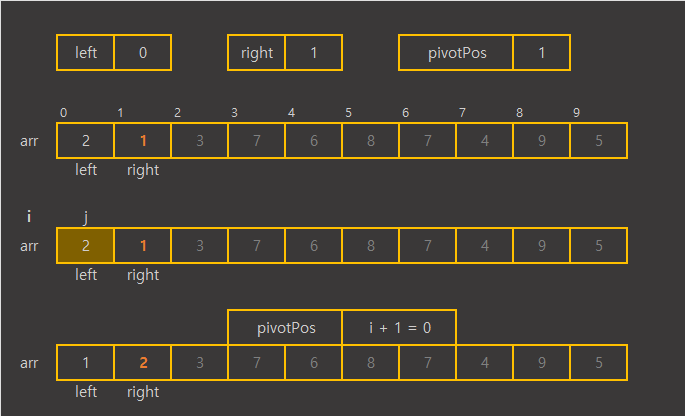
배열 범위 내에서
기준 값인 pivot보다 큰 값이 나오면 지나가고,
pivot보다 작은 값이 나오면 i를 1증가시킨 후 i와 교체하며
pivot보다 작은 값들을 배열의 왼쪽 구간에 두게 된다.
i는 탐색이 끝난 후 pivot의 위치가 될 값으로,
탐색중엔 pivot보다 작은값과 큰 값을 구분하는 용도로 사용된다.
탐색 중 i의 위치는
pivot보다 작은 값들 중 마지막으로 정리 된 값의 위치이다.
private int[] quickSort(int[] arr) {
quickSortRecursive(arr, 0, arr.length - 1);
return arr;
}
private void quickSortRecursive(int[] arr, int left, int right) {
if (left >= right)
return;
int pivotPos = partition(arr, left, right);
quickSortRecursive(arr, left, pivotPos - 1);
quickSortRecursive(arr, pivotPos + 1, right);
}
// 정렬 구현
// 기준점 : 가장 오른쪽 요소
// 왼쪽 끝에서부터 pivot과 비교하며 정렬
private int partition(int[] arr, int left, int right) {
int pivot = arr[right]; // 가장 오른쪽 요소를 기준값으로 사용
int i = left - 1;
for (int j = left; j < right; j++) {
if (arr[j] < pivot) {
i++;
swap(arr, i, j);
}
}
// pivot 제자리로.
int pivotPos = i + 1;
swap(arr, pivotPos, right);
return pivotPos;
}실행 확인!
[ arr ]___________🚩 [1, 2, 3, 4, 5, 6, 7, 7, 8, 9]처음 왼쪽 구간 정렬 구현 묘사