편차 : 값 – 평균
분산 : 편차 제곱의 평균
-> df.price.var()
표준편차 : 루트 분산
-> df.price.std()
모집단 population: 연구의 관심이 되는 집단 전체
표본 sample: 특정 연구에서 선택된 모집단의 부분 집합
파라미터 parameter: 어떤 시스템의 특성을 나타내는 값
모수: 모집단 population의 파라미터 → 모집단의 특성을 나타내는 값
예시:
• 모집단의 평균 (모평균)
• 모집단의 분산 (모분산)
통계량 sample statistic : 표본에서 얻어진 수로 계산한 값 (=통계치)
예시:
• 표본의 평균 (표본평균)
• 표본의 분산 (표본분산)
표집 sampling : 모집단에서 표본을 추출하는 절차. "표본 추출"이라고도 함
- 표집 단위 sampling unit: 측정의 단위 (예: 개인, 상품 등)
- 표집틀 sampling frame: 표집 대상의 목록
추정 estimation : 통계량으로부터 모수를 추측하는 절차
• 점 추정 point estimate: 하나의 수치로 추정
• 구간 추정 interval estimate: 구간으로 추정
신뢰구간 confidence interval
• 대표적인 구간 추정 방법
• 모수가 있을 법한 범위로 추정
• 신뢰구간 = 통계량±오차범위
• 95%(신뢰수준) 신뢰구간 = 95%의 경우에 모수가 추정된 신뢰구간에 포함됨
신뢰 수준 confidence level
• 신뢰구간에 모수가 존재하는 표본의 비율
- 신뢰수준이 높음 → 많은 표본을 포함 → 더 넓은 오차범위 → 정보가 적음
- 신뢰수준이 낮음 → 적은 표본을 포함 → 더 좁은 오차범위 → 정보가 많음
• 신뢰구간이 좁으면 신뢰수준이 낮으므로 타협이 필요 - 교과서적으로는 95%, 99% 등을 추천하나 절대적 기준은 없음
- 감수할 수 있는 수준에서 결정
신뢰구간에 영향을 주는 요소
• 신뢰구간이 좁을 수록 예측된 모수의 범위가 좁으므로 유용
• 신뢰수준 낮추기: 큰 의미는 없음
• 표본의 변산성 낮추기:
- 실험과 측정을 정확히 해서 변산성을 낮춤
- 데이터에 내재한 변산성은 없앨 수 없음
• 표본의 크기를 키우기 - 가장 쉬운 방법이나 시간과 비용이 증가
부트스트래핑 bootstrapping
• 평균과 달리 중간값, 최빈값 등의 통계량은 표집분포의 형태를 간단히 알기 어
려움
• 표본이 충분히 크면 부트스트래핑이라는 시뮬레이션 기법을 사용해서 신뢰구
간을 추정
통계적 가설 검정 statistical hypothesis testing
• Karl Pearson, Ronald Fisher 등 통계학의 초기 인물들이 개발한 절차
• 반증주의 철학에 기반하고 있어 일반적인 과학적 가설 검정과 다름
• 많은 비판이 있으나, 오랫동안 쓰여왔기 때문에 여전히 널리 쓰임
귀무가설과 대립가설
𝐻0 귀무가설 null hypothesis
• 기각하고자 하는 가설
• 차이가 없다, 똑같다와 같은 형태
• 특별한 증거가 없으면 참으로 간주
𝐻1대립가설 alternative hypothesis
• 주장하고자 하는 가설
• 차이가 있다, 다르다와 같은 형태
• 충분한 증거가 필요
통계적 가설 검정의 논리
• 귀무가설을 기각하는 논리:
- A → B라는 명제는 not B → not A라는 대우명제와 동치
- 귀무가설이 참이면(A), 현재 결과가 나올 확률이 높다(B)
- 현재 결과가 나올 확률이 낮으면(not B), 귀무가설이 거짓이다.(not A)
• 귀무가설을 채택하지 않는 논리: - 통계적 가설검정을 만든 로널드 피셔의 반증주의적 과학철학을 반영
- A → B라는 명제가 성립해도, B → A가 반드시 성립하는 것은 아님
- 귀무가설이 참이면(A), 현재 결과가 나올 확률이 높다(B)
- 현재 결과가 나올 확률이 높아도(B), 귀무가설이 참(A)이라고 할 수는 없음
유의수준과 p 값
• p 값: 귀무가설을 바탕으로 데이터에서 관찰된 결과와 그 이상의 극단적 결과가 나
올 확률을 계산한 것
• 유의수준(significance level)
• p 값을 바탕으로 높고 낮음을 판정하는 기준.
• 그리스 문자 𝛼(알파)로 표기
• 보통 5%(=0.05)를 사용
• 100% - 신뢰수준
• 𝑝 < 𝛼면 귀무가설을 기각 → 대립가설을 채택
p와 유의수준의 비교
p > 유의수준
• 결론을 유보한다
• 결론을 내릴 필요가 있을 경우, 데이터를 더 모은다
• 단, 반복해서 가설검정을 할 경우 유의수준을 조정한다
p < 유의수준
• 귀무가설을 기각한다
• 대립가설을 채택한다
• 흔히 "통계적으로 유의하다 statistically significant"라고 표현(현실적으로 유의한 것은 아님)
• 어떠한 관계가 있다고 주장하기에 표본의 크기가 충분하다는 것으로 이해할 수 있음
• 귀무가설이 참일 경우, 1종 오류는 유의수준만큼 발생
• 유의수준을 낮추면 1종 오류가 감소하고, 2종 오류가 증가
5% 낮다 높다의 기준 : 유의수준
신뢰구간에 있으면 p값 > 유의수준
신뢰구간에 없으면 p값 < 유의수준
상관 계수 correlation coefficient
• 두 변수의 연관성을 -1 ~ +1 범위의 수치로 나타낸 것
• 두 변수의 연관성을 파악하기 위해 사용
- 어휘력과 독해력의 관계
- 주가와 금 가격의 관계
- 엔진 성능과 고객만족도의 관계
상관계수의 해석
• 부호: - +: 두 변수가 같은 방향으로 변화(하나가 증가하면 다른 하나도 증가)
- -: 두 변수가 반대 방향으로 변화(하나가 증가하면 다른 하나는 감소)
• 크기: - 0: 두 변수가 독립, 한 변수의 변화로 다른 변수의 변화를 예측하지 못함
- 1: 한 변수의 변화와 다른 변수의 변화가 정확히 일치
상관계수가 커지면 p밸류는 작아짐
데이터가 많아져도 p밸류는 작아짐
상관계수 보는법
import pingouin as pg
pg.corr(df.price, df.mileage)결과

r= 표본상관계수, (모상관계수 -0.74 ~ -0.61)
귀무가설 : 모상관계수 = 0.0
(p=0.00.. < 0.05)
결론 -> 귀무가설 기각(모상관계수 != 0)
sp.SPX.diff() -> 차분
: 한달씩 기준으로 상승됐냐 하락됐냐 따짐.
회귀분석
지도학습 supervised learning
• 독립변수 x를 이용하여 종속변수 y를 예측하는 것
- 통계학에서 예측(prediction)은 어떤 값에 대한 추론을 의미 (시간적인 의미 X)
- 지도학습에서 예측은 변수들 사이의 패턴을 파악하여 한 변수로 다른 변수를 추론하는 것
- 시계열 분석 등에서 하는 미래에 대한 예측은 forecasting이라고 구분
• 독립변수 independent variable: 예측의 바탕이 되는 정보, 인과관계에서 원인, 입력값
• 종속변수 dependent variable: 예측의 대상, 인과관계에서 결과, 출력값
선형 모형
𝑦 = 𝑤𝑥 + 𝑏
• 𝑦 : 𝑦의 예측치
• 𝑥: 독립변수
• 𝑤: 가중치 또는 기울기
• 𝑏: 절편(𝑥 = 0 일 때, y의 예측치)
from statsmodels.formula.api import ols
m = ols("price ~ mileage", data = df).fit()
m.summary()
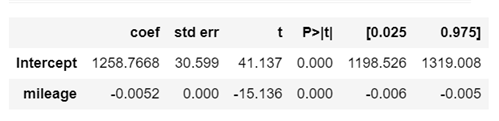
상관분석 : 서로 관계가 있는가?
회귀분석 : x를 이용해서 y를 예측하려면 ?
더미 코딩 dummy coding
• 범주형 변수에 범주가 k개 있을 경우 k-1개의 더미 변수를 대신 투입
• 범주 중에 하나를 기준 reference로 지정
- 기본적으로 ABC 순으로 먼저 나오는 것이 기준(변경할 수도 있음)
• 기준를 제외한 범주들은 범주별로 더미 변수를 하나씩 가짐 - 더미변수는 해당 범주일 경우에만 고려
- 더미변수의 기울기는 기준과의 차이를 의미
범주가 2개인 경우
• ABC 순으로 Avante가 기준
• K3의 더미 변수 추가
• 0 = No, 1 = Yes로 이해
Q. 데이터 숫자가 273개 밖에 없는데 회귀분석이 유의미 한가요? 혹시 유의미한 분석 결과를 내기 위해 필요한 최소한의 데이터 숫자가 정해져 있을까요?
-> 유의미한 분석은 없음, 모든 분석은 유의미함. 데이터 1개라도 유의미함.
데이터가 적어도됨 하지만 결론이 잘 안나옴.
왜 많아야 하냐? -> 귀무가설을 기각하고 결론을 내려고
결론이 난다 -> 충분한 분석을 한 것
ols("marriage ~ rating + overtime", data = hr).fit().summary()
