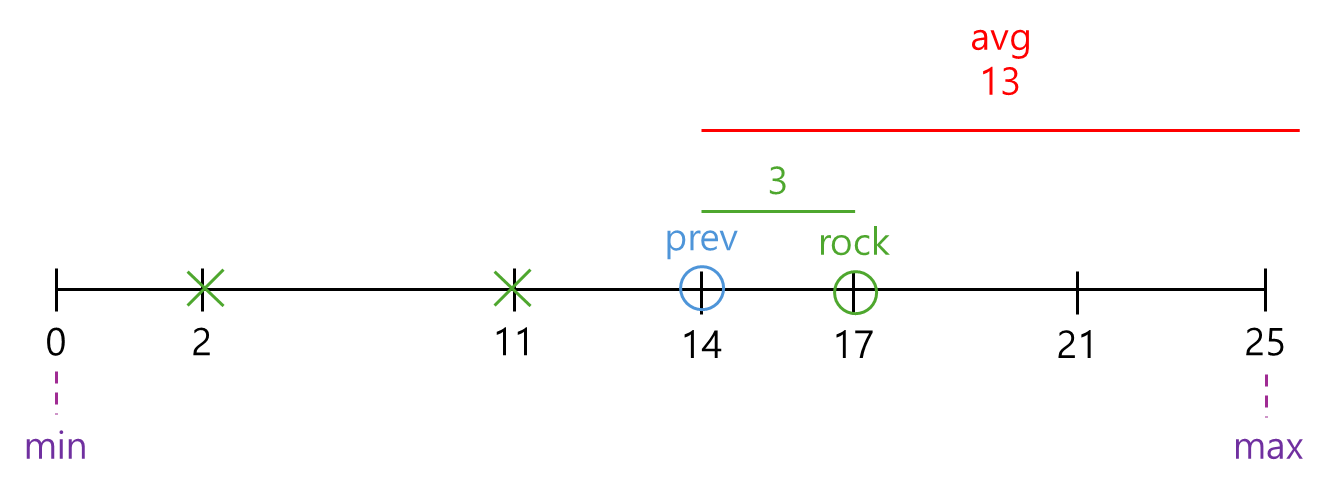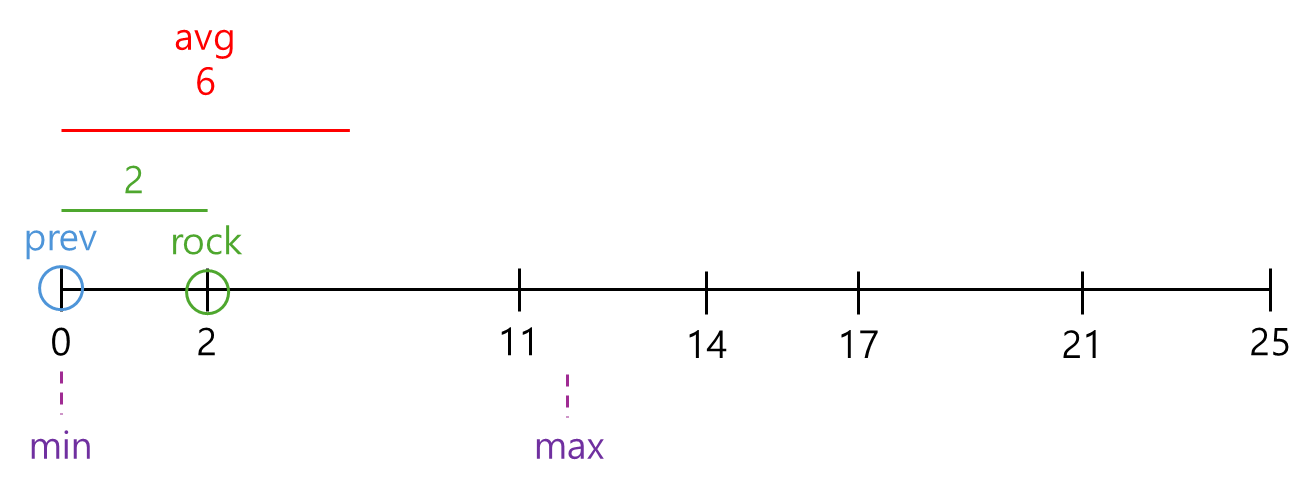[알고리즘/C++] 프로그래머스 - 징검다리 (Lv.4, 이분탐색)

✏️ 풀이 방법.. 인척 하는 이해 방법
풀면서도 풀고 나서도 무슨 말인지 하나도 이해를 못했다.
다른 분들의 코드와 주석을 50번쯤 다시 보고, 직접 그림을 그려 보고서야
아 이건가? 싶었다.
결국 해답은 중간값(mid=avg)이 정답이 되는 것이다.
이분탐색 방식으로 거리값을 계속 반으로 줄여가면서 돌 두개를 뺄 수 있는
거리의 최소값을 구하는 것.

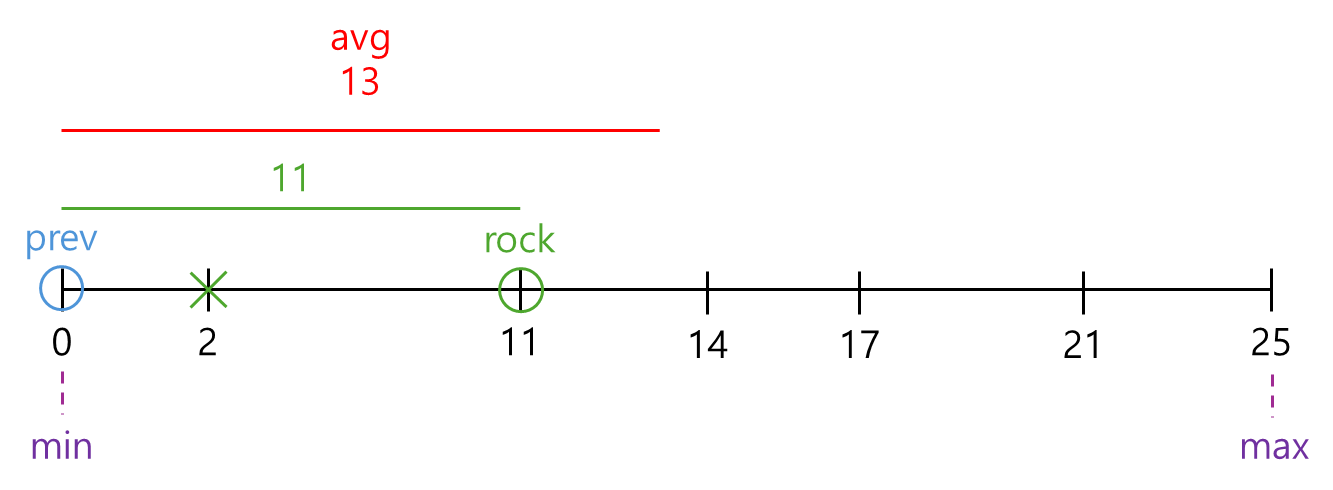
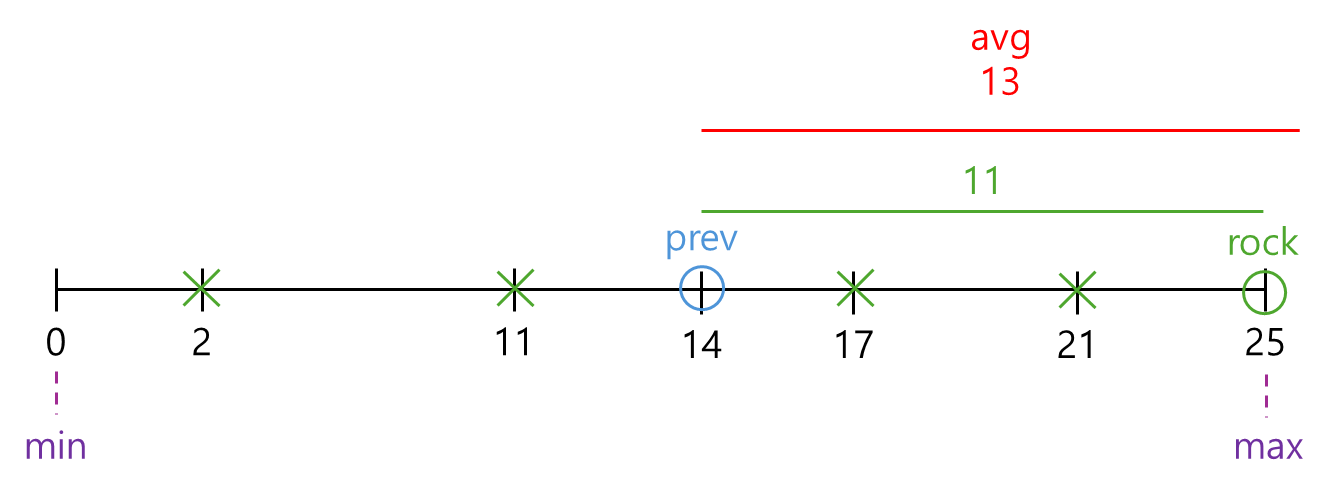
✏️ 그림으로 이해하기

🔼 거리가 2? avg보다 작네! 돌 빼!

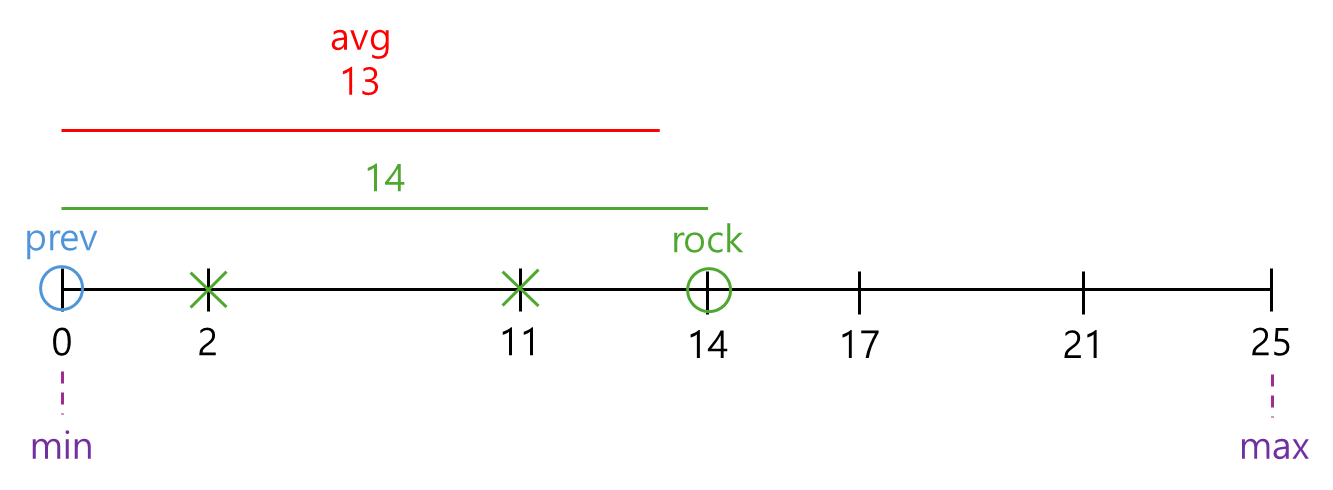
🔼 거리가 11? avg보다 작네! 돌 빼!

🔼 거리가 14? avg보다 크네.. 일단 한번 봐준다!

🔼 거리가 3? avg보다 작네! 돌 빼!

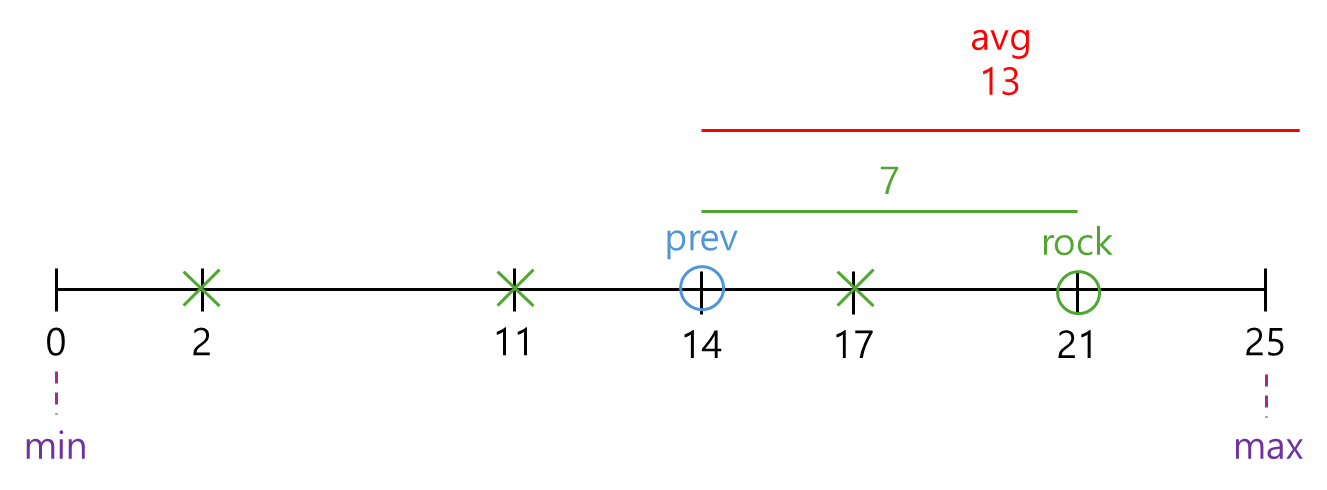
🔼 거리가 7? avg보다 작네! 돌 빼!

거리가 11? avg보다 작네! 돌 빼!

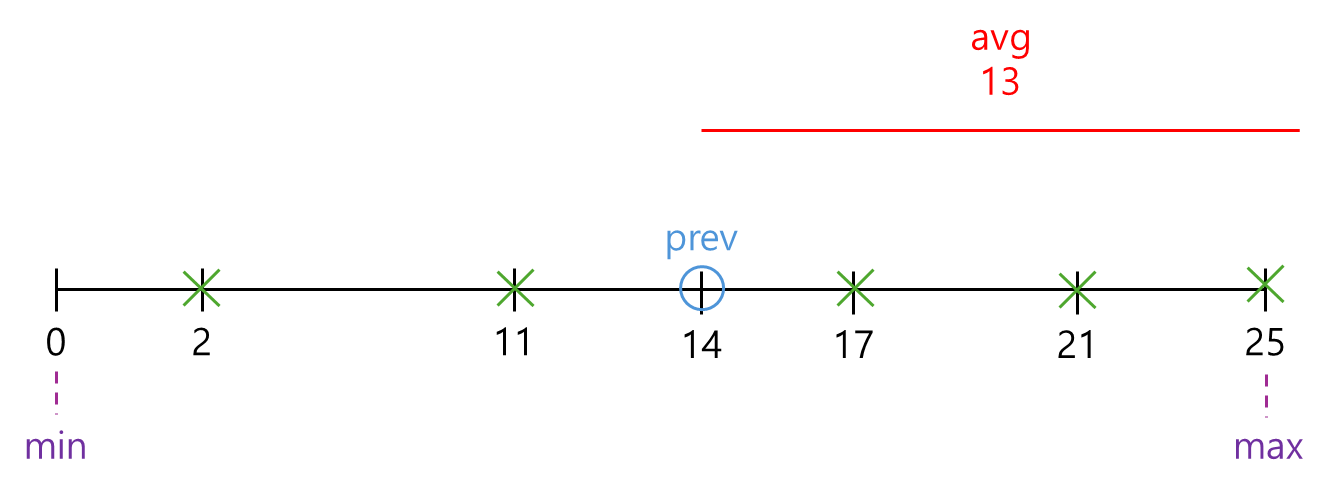
🔼 어? 돌을 5개나 뺐네.. 거리 줄여야겠다
👉 maxDist = 13-1 = 12
👉 avgDist = (0 + 12) / 2 = 6

🔼 반복..
사실상 min, max는 거리만 가늠하는 용이므로 위 그림 내에서 의미는 없다.

#include <string>
#include <vector>
#include <algorithm>

using namespace std;

int solution(int distance, vector<int> rocks, int n)
{
    int answer = 0;
	
    sort(rocks.begin(), rocks.end());	// 정렬 (이분탐색의 기본 조건)
    rocks.push_back(distance);	// 도착지점과의 거리 검사도 필요함

    int minDist = 1;
    int maxDist = distance;

    while (minDist <= maxDist)
    {
        int prevRock = 0;	// 체크 기준이 되는 돌. 맨 처음엔 시작점
        int avgDist = (minDist + maxDist) * 0.5;

        int removeCnt = 0;	// 지금까지 제거한 돌 개수
        for (int rock : rocks)
        {
        	// (다음 돌 - 지금 돌 거리) < 거리
            if (rock - prevRock < avgDist)
            {
                removeCnt++;	// 방 빼
            }
            else
            {
                prevRock = rock;	// 다음번엔 안 봐준다
            }
        }

        if (removeCnt <= n)	// 뺄 수 있는 개수만큼 방 뺐으면
        {
            answer = max(answer, avgDist);	// 정답이 최솟값 중 최대값을 구하는 것이므로
            minDist = avgDist + 1;	// 최소 기준값 변경
        }
        else
        {
            maxDist = avgDist - 1;	// 최대 기준값 변경
        }
    }

    return answer;
}

✏️ 풀고 나서
분류가 이분탐색이 아니었다면 이분탐색으로 풀 생각을 못했을 것 같다.
다만 다른 블로그 글들을 보다 보니, 예제의 범위가 생각보다 너무 크다~ 싶으면 눈치껏 이분탐색으로 풀면 된다고 한다!