저번에 float 형의 형변환의 값이 부정확하다는 글을 쓴적이 있었는데,
그 이후에 문득 떠오른것이 '부동소수점의 오차' 였다.
기본 개념으로 다 배웠던 사실인데 잊고 있었다.
복습하는 겸 다시 잊지 않기 위해 정리해두려고 한다.
부동소수점 (floating point)
유효숫자를 나타내는 가수와 소수점의 위치를 나타내는 지수로 표현한다.

예를 들어, 3.75을 부동소수점 float 형 (32비트)으로 표현한다면
양수이므로 부호비트는 0

3 = 2 + 1 이므로 11⑵
0.75 = 0.5 + 0.25 이므로 0.11⑵
즉, 이진수 11.11⑵ 이 된다.
11.11⑵ = 1.111⑵ × 2¹
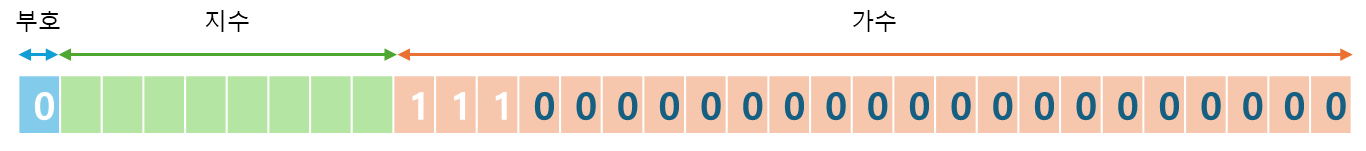
지수가 1이므로 Bias 127을 더해 128 = 10000000⑵
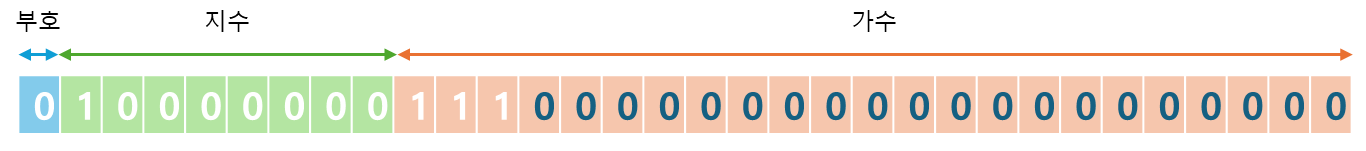
아래 사이트에서 편하게 변환해 볼 수 있다.
https://www.h-schmidt.net/FloatConverter/IEEE754.html
부동소수점의 0.1 표기
오차를 확인하기 위해 간단히 0.1을 부동소수점으로 표현해보기로 한다.
2진수로 명확히 표기할수 있는 소수는 1/(2의 제곱수) = ½, ¼, ⅛ ... 로 표현할수 있는 숫자만이다.
⅛ = 0.125, 1/16 = 0.0625 이므로 0.1은 그 사이 어딘가의 값이다.
👀 참고
https://velog.io/@nimo6289/%EB%B6%80%EB%8F%99%EC%86%8C%EC%88%98%EC%A0%90
대략적인 값은 0.00011001100110011001100......⑵이 된다.
0.00011001100110011001100⑵ = 1.1001100110011001100 2-⁴
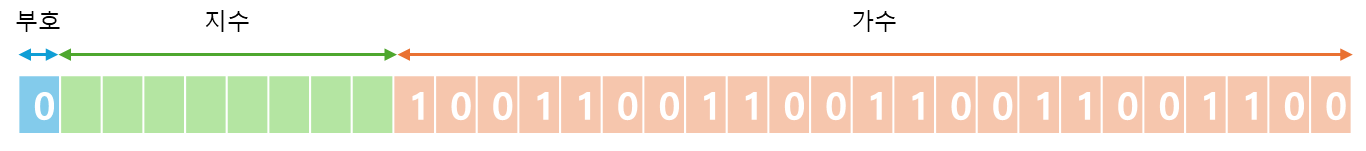
지수 = 127 + (-4) = 123 = 1111011⑵
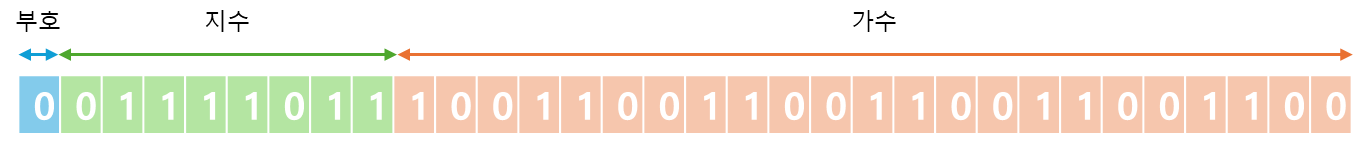
결론적으로, 0.00011001100110011001100⑵ = 0.100000001490116119384765625이 되므로 정확하게 0.1의 값을 저장할수 없다.