[알고리즘/C++] 프로그래머스 - 두 원 사이의 정수 쌍 (원의 공식)

✏️ 풀이 방법
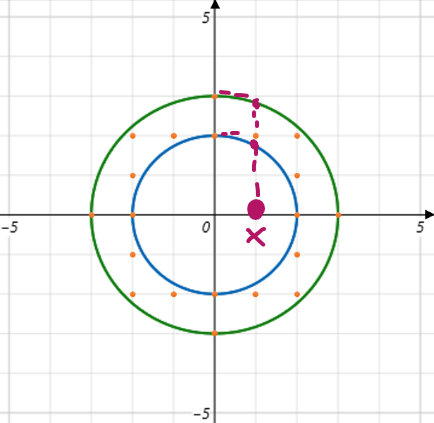
큰 원의 반지름 안에 있는 정점과 원점을 가지고 점과 점사이 거리 공식을 사용했었는데 시간초과가 났다.
찾아보니 원의 공식을 사용해 임의의 x 좌표에서의 원 위의 정점을 구하면 편하게 계산할 수 있는 것 같았다.

해당 두 좌표를 계산하고 그 사이의 y 값의 개수를 구하면 된다.

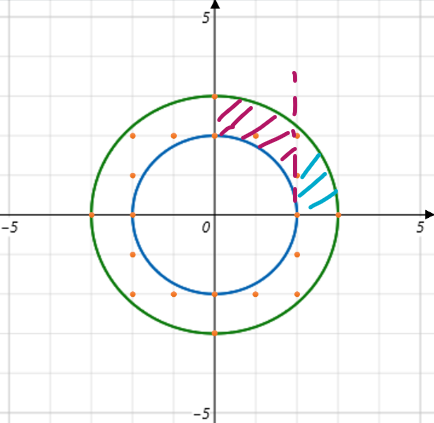
원1과 원2 사이의 값을 먼저 계산하고, 이후 축과 원2 사이의 값을 계산한다.
이렇게 구하고 나면 1사분면 위의 정점 + x축 위의 정점 + y축 위의 정점이 나오는데
축 위의 정점들은 * 4 로 처리했을때 중복되므로 한번 빼 주었다.

double DistanceY(int r, int x)
{
    return sqrt( pow(r, 2) - pow(x, 2) );
}

long long solution(int r1, int r2)
{
    long long answer = 0;

    // 좌표계에 있는 정점 개수
    long long points = 0;
    for (int x = 0; x <= r1; ++x)
    {
        double r2Y = floor(DistanceY(r2, x));
        double r1Y = ceil(DistanceY(r1, x));
        points += (r2Y - r1Y) + 1;
    }

    for (int x = r1 + 1; x <= r2; ++x)
    {
        double r2Y = floor(DistanceY(r2, x));
        points += r2Y + 1;
    }

    answer += (points - (r2 - r1 + 1)) * 4;

    return answer;
}