[알고리즘] 정렬 (Sorting)

윤여준·2023년 1월 5일

알고리즘 정렬

알고리즘

목록 보기

1/1

대표적인 정렬 알고리즘의 종류

버블 정렬 (Bubble Sort)
선택 정렬 (Selection Sort)
삽입 정렬 (Insertion Sort)
힙 정렬 (Heap Sort)
병합 정렬 (Merge Sort)
퀵 정렬 (Quick Sort)
기수 정렬 (Radix Sort)

버블 정렬

버블 정렬은 인접한 두 개의 데이터를 비교해가면서 정렬을 진행하는 방식이다.

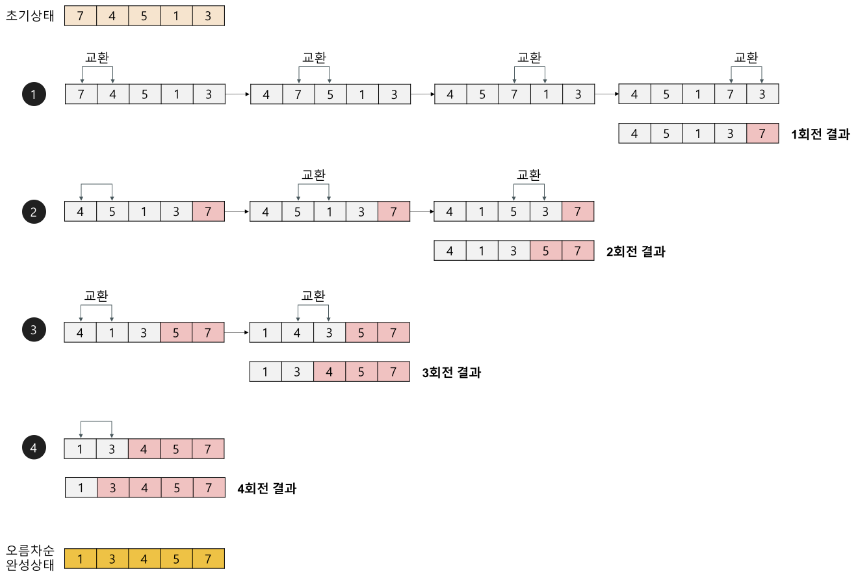
정렬의 우선순위가 가장 낮은 값을 맨 뒤로 보내는 것이 핵심이다.

위의 그림을 보자.

초기 상태는 7,4,5,1,3이다.

맨 앞에서부터 비교와 교환을 진행한다. 만약 앞의 원소가 뒤의 원소보다 크다면 교환을 해주고 아니면 그냥 다음 원소로 넘어간다. 그 결과 위와 같이 정렬이 된다.

위 그림은 버블 정렬이 일어나는 모습이다. 원소의 이동이 마치 거품이 올라오는 것처럼 보여서 버블 정렬이라는 이름이 붙었다.

버블 정렬의 시간복잡도

정렬 알고리즘의 성능은 비교 연산과 데이터의 이동을 위한 대입 연산을 근거로 판단하는 것이 일반적이다. 비교 연산과 대입 연산이 정렬 과정의 핵심 연산이기 때문이다.

아래의 코드는 버블 정렬을 구현할 때 작성하게 되는 코드의 일부이다. 버블 정렬의 비교 횟수는 다음 반복문 안에 위치한 if문의 실행 횟수를 기준으로 계산할 수 있다.

for (i = 0; i < n - 1; i++) {
	for (j = 0; j < (n - i) - 1; j++) {
    	if (arr[j] > arr[j + 1]) { ... } // 비교 연산이 발생하는 장소
    }
}

위 코드에서 if문의 실행 횟수는 다음과 같다.

$(n - 1) + (n - 2) + ... + 2 + 1 = \sum\limits_{i = 1}^{n-1}i = {n(n - 1) \over 2} = {n^2 - n \over 2}$

따라서 버블 정렬의 비교 연산에 대한 빅-오는 최악의 경우와 최선의 경우 구분 없이 다음과 같다.

$O(n^2)$

다음으로 버블 정렬의 대입 연산에 대한 빅-오를 구해보자.

최선의 경우와 최악의 경우를 나눌 수 있다. 최선의 경우는 데이터가 이미 정렬되어 있는 경우로, 데이터의 교환이 한 번도 일어나지 않는다.

최악의 경우는 데이터가 역순으로 저장되어 있는 상태이다. 이런 상태에서는 비교 횟수와 교환 횟수가 일치한다. 따라서 데이터 이동 연산에 대한 빅-오는 최악의 경우에 $O(n^2)$ 이다.

선택 정렬

선택 정렬은 정렬 순서에 맞게 하나씩 선택해서 옮기는, 옮기면서 정렬이 되게 하는 알고리즘이다.

선택 정렬의 과정은 다음과 같다.

주어진 배열 중에 최솟값을 찾는다.
그 값을 맨 앞에 위치한 값과 교체한다.
맨 처음 위치를 뺀 나머지 배열을 같은 방법으로 교체한다.

선택 정렬의 시간복잡도

선택 정렬의 비교 연산의 실행 횟수를 구하기 위해서 선택 정렬 구현 코드의 일부를 살펴보자.

for (i = 0; i < n - 1; i++) {
	maxIdx = i;
    
    for (j = 1 + 1; j < n; j++) {
    	if (arr[j] < arr[maxIdx]) // 선택 정렬의 비교 연산
        	maxIdx = j;
    }
}

위 코드에서 비교 연산이 실행되는 횟수는 다음과 같다.

$(n - 1) + (n - 2) + ... + 2 + 1$

이는 버블 정렬의 경우와 똑같다. 따라서 선택 정렬의 비교 연산의 시간복잡도 역시 최선의 경우와 최악의 경우 구분 없이 $O(n^2)$ 이다.

이어서 대입 연산의 실행 횟수를 구해보자.

for (i = 0; i < n - 1; i++) {
	// 위와 동일
    ...
    
    temp = arr[i];
    arr[i] = arr[maxIdx];
    arr[maxIdx] = temp;
}

대입 연산이 존재하는 위치를 보면 바깥쪽 for문에 존재하고 있다. 따라서 선택 정렬의 경우 n - 1회의 교환이 일어나므로, 데이터 이동횟수는 이의 세 배인 3(n - 1)이 된다. 따라서 선택 정렬의 데이터 이동 연산에 대한 시간복잡도는, 최악의 경우와 최선의 경우 구분 없이 $O(n)$ 이다.

삽입 정렬

삽입 정렬은 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여 자신의 위치를 찾아 삽입하여 정렬을 하는 알고리즘이다.

정렬 과정은 다음과 같다.

2번째 위치(index)의 값을 temp에 저장한다.
temp와 이전에 있는 원소들과 비교하며 삽입해나간다.
'1'번으로 돌아가 다음 위치(index)의 값을 temp에 저장하고, 반복한다.

삽입 정렬의 시간복잡도

삽입 정렬의 시간복잡도 분석을 위해 아래의 코드를 살펴보자.

for (i = 1; i < n; i++) {
	...
    for (j = i - 1; j >= 0; j--) {
    	if (arr[j] > insData)
        	arr[j + 1] = arr[j];
        else
        	break;
    }
}

정렬 대상이 완전히 정렬된 상태라면, 안쪽 for문의 if/else문의 조건은 항상 거짓이 되어 break문을 실행하게 된다. 따라서 데이터의 이동도 발생하지 않고 if/else문의 조건비교도 바깥쪽 for문의 반복 횟수 이상 진행되지 않는다.

하지만 최악의 경우를 고려하면, 앞의 두 정렬 방법과 다를 바 없다. 최악의 경우 안쪽 for문의 if/else문의 조건은 항상 참이 되어 break문을 단 한번도 실행하지 않는다. 따라서 바깥쪽 for문의 반복 횟수와 안쪽 for문의 반복 횟수를 곱한 수만큼 비교연산과 이동연산이 진행되므로, 이를 근거로 비교 연산과 이동 연산에 대한 빅-오가 $O(n^2)$ 임을 알 수 있다.

힙 정렬

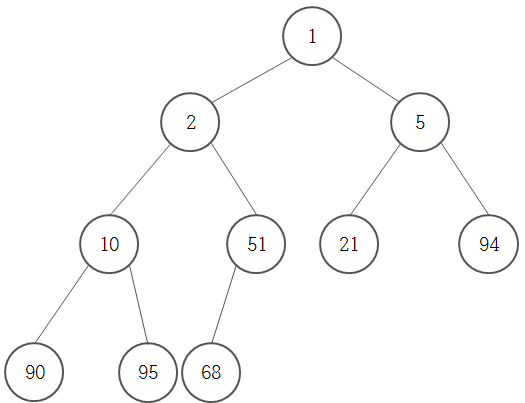
힙 정렬은 "힙의 루트 노드에 저장된 값이 가장 커야 한다" 라는 최대 힙의 특성을 활용하여 정렬하는 방식이다.

위의 특성을 다음과 같이 바꿀 수 있다. "힙의 루트 노드에 저장된 값이 정렬 순서상 가장 앞선다."

힙 정렬은 단순히 힙에 데이터를 모두 넣었다가 힙에서 다시 데이터를 모두 꺼내면 된다.

힙 정렬의 시간복잡도

힙의 데이터 저장 및 삭제의 시간복잡도는 다음과 같다.

힙의 데이터 저장 시간복잡도 - $O(\log_2{n})$
힙의 데이터 삭제 시간복잡도 - $O(\log_2{n})$

따라서 삽입과 삭제를 하나의 연산으로 묶는다면, 이 연산에 대한 시간복잡도는 $O(2\log_2{n})$ 이다. 하지만 숫자 2는 빅-오에서 무시할만한 수준이므로 삽입과 삭제를 하나의 연산으로 묶더라도 이 연산에 대한 시간복잡도는 여전히 $O(\log_2{n})$ 이다.

그러면 정렬 과정에 대한 시간복잡도를 구해보자. 정렬 대상의 수가 n개라면 총 n개의 데이터를 삽입 및 삭제해야하므로 위의 빅-오에 n을 곱하면 된다. $O(n\log_2{n})$

병합 정렬

병합 정렬은 분할 정복(divide and conquer)이라는 알고리즘 디자인 기법에 근거하여 만들어진 정렬 방법이다.

분할 정복이란 말 그대로 복잡한 문제를 복잡하지 않은 문제로 분할하여 정복하는 방법이다. 단, 분할해서 정복했으니 정복한 후에는 결합의 과정을 거쳐야 한다. 즉, 다음 3단계를 거치도록 알고리즘을 디자인 하는 것을 분할 정복법이라고 한다.

분할(Divide) - 해결이 용이한 단계까지 문제를 분할해 나간다.
정복(Conquer) - 해결이 용이한 수준까지 분할된 문제를 해결한다.
결합(Combine) - 분할해서 해결한 결과를 결합하여 마무리한다.

분할 정복은 다음과 같은 논리로 병합 정렬에 적용되었다.
"8개의 데이터를 동시에 정렬하는 것보다, 이를 둘로 나눠서 4개의 데이터를 정렬하는 것이 쉽고, 또 이들 각각을 다시 한번 둘로 나눠서 2개의 데이터를 정렬하는 것이 더 쉽다"

따라서 병합 정렬은 우선 데이터가 1개가 남을 때까지 둘로 분할한다. 그리고서 다시 합치는 병합을 진행하는데, 이때 정렬 순서를 고려해서 병합한다. 모든 데이터를 병합할 때까지 병합을 진행한다. 병합 정렬의 과정은 아래의 그림을 참고하면 된다.

처음부터 하나씩 나누면 될 것 같은데 왜 하나씩 구분이 될 때까지 둘로 나누는 과정을 반복할까? 그 이유는 바로 재귀적 구현을 하기 위해서다.

병합 정렬의 시간복잡도

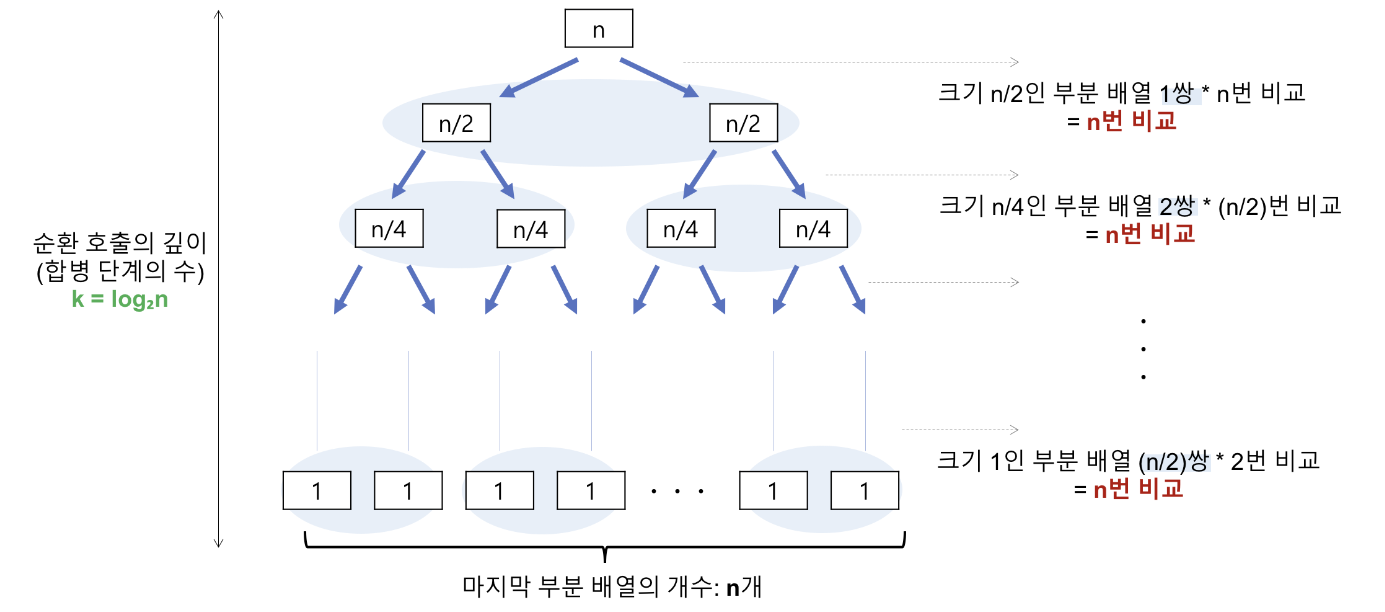
병합 단계의 높이는 $\log_2{n}$ 이고 각 단계에서 정렬에 필요한 반복 횟수는 $n$ 이다. 따라서 시간복잡도는 높이 * 반복 횟수인 $O(n\log_2{n})$ 이다.

퀵 정렬

퀵 정렬도 병합 정렬과 마찬가지로 분할 정복에 근거하여 만들어진 정렬 방법이다.

정렬 과정은 다음과 같다.

리스트 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗이라고 한다.
피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 리스트를 둘로 나눈다. 이렇게 리스트를 둘로 나누는 것을 분할이라고 한다.
분할된 두 개의 작은 리스트에 대해 재귀적으로 이 과정을 반복한다. 재귀는 리스트의 크기가 0이나 1이 될 때까지 반복된다.

퀵 정렬의 시간복잡도

최선의 경우와 최악의 경우를 나눠서 생각해보자.

먼저 최선의 경우, 둘로 나뉘는 횟수를 k라고 할 때, 데이터의 수 n과의 관계는 $k = \log_2{n}$ 이다. 따라서 퀵 정렬에서의 비교 연산 횟수는 $n\log_2{n}$ 이고, 이로 인해 비교 연산의 빅-오는 $O(n\log_2{n})$ 이다.

최악의 경우는 이미 데이터들이 정렬되어 있으면서 피벗이 가장 작은 값으로 결정되는 경우이다. 이때 둘로 나뉘는 횟수 k와 데이터의 수 n과의 관계는 $k = n$ 이다. 따라서 최악의 경우의 비교 연산 횟수에 대한 빅-오는 $O(n^2)$ 이다.

하지만 최악의 경우로 퀵 정렬을 평가하지는 않는다. 실제로 퀵 정렬은 $O(n\log_2{n})$ 의 복잡도를 갖는 다른 정렬 알고리즘과 비교했을 때에도 평균적으로 제일 빠른 것으로 알려져 있다. 그 이유는 중간에 가까운 피벗을 선택하면 늘 최선의 경우를 보이는 것은 아니지만 최선의 경우에 가까운 성능을 평균적으로 보이기 때문이다.

정리하면, 퀵 정렬은 시간 복잡도가 $O(n\log_2{n})$ 인 알고리즘이다. 하지만 데이터의 이동이 데이터의 비교에 비해 현저히 적게 일어나고, 별도의 메모리 공간을 요구하지 않으므로 동일한 빅-오를 갖는 다른 정렬 알고리즘 중에서 평균적으로 가장 빠른 정렬 속도를 보이는 알고리즘이다.

기수 정렬

기수 정렬은 정렬 순서상 앞서도 뒤섬의 판단을 위한 비교 연산을 하지 않는다.

또한 정렬 알고리즘의 이론상 성능의 한계로 알려진 $O(n\log_2{n})$ 을 넘어설 수 있는 유일한 알고리즘이다.

물론 적용할 수 있는 범위가 제한적이라는 한계가 있다. 데이터의 길이가 같은 데이터들만 정렬할 수 있다.

그렇다면 어떻게 정렬을 할 수 있을까? 정렬 과정에 대해 알아보기 전에 우선 기수가 무엇인지부터 알아보자.

기수(radix)란 주어진 데이터를 구성하는 기본 요소를 말한다. 예를 들어 2진수는 0과 1의 조합으로 데이터를 표현하니 2진수의 기수는 0과 1이다. 유사하게 10진수는 0부터 9까지의 숫자 조합으로 데이터를 표현하니 0부터 9까지의 숫자가 10진수의 기수가 된다.

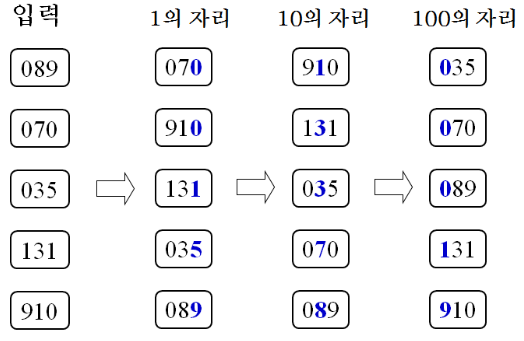
이제 기수 정렬의 과정을 알아보자. 아래의 과정은 LSD 기수 정렬 방법이다. LSD는 Least Significant Digit의 약자로 덜 중요한 자릿수에서부터 정렬을 진행해 나간다는 의미를 담고 있다.

기수의 개수만큼 버킷(양동이)을 준비한다. (예: 2진수 - 2개의 버킷, 10진수 - 10개의 버킷)
모든 데이터에 대하여 가장 낮은 자릿수에 해당하는 버킷에 차례대로 데이터를 넣는다.
첫번째 버킷에서부터 시작해서 순서대로 데이터를 꺼낸다. 이때 꺼낸 데이터들은 버킷에 넣을 때 기준 삼았던 자릿수를 기준으로 정렬되어 있다.
자릿수의 단계를 하나씩 높혀서 2번과 3번 과정을 반복한다. 가장 높은 자릿수의 정렬이 일어날 때까지 반복한다.

MSD 기수 정렬 방법도 있다. MSD는 Most Significant Digit의 약자로 중요한 자릿수에서부터 정렬을 진행해 나간다는 의미이다.

우리의 직관에는 MSD 기수 정렬 방법이 어울리지만, 프로그래밍으로 구현하기에는 LSD 기수 정렬 방법이 수월하다.

기수 정렬의 시간복잡도

기수 정렬의 핵심은 비교 연산이 아니다. 버킷으로의 데이터 삽입과 추출이 핵심이다. 따라서 기수 정렬의 시간 복잡도는 삽입과 추출의 빈도수를 대상으로 결정해야 한다.

이를 위해서 기수 정렬 구현 코드의 일부를 살펴보자.

void RadixSort(int arr[], int num, int maxLen) {
	....
    // 가장 긴 데이터의 길이만큼 반복
    for (pos = 0; pos < maxLen; pos++) {
    	// 정렬 대상의 수만큼 버킷에 데이터 삽입
    	for (di = 0; di < num; di++) {
        	// 버킷으로의 데이터 삽입 진행
        }
        
        // 정렬 대상의 수만큼 버킷으로부터 데이터 추출
        for (bi = 0, di = 0; bi < BUCKET_NUM; bi++) {
        	// 버킷으로부터의 데이터 추출 진행
        }
        ....
    }
}

위 코드에서 버킷을 대상으로 하는 데이터의 삽입과 추출을 한 쌍의 연산으로 묶으면, 이 한 쌍의 연산이 수행되는 횟수는 $maxLen * num$ 이다. 따라서 정렬 대상의 수가 n이고, 모든 정렬 대상의 길이가 l이라 할 떄, 시간 복잡도에 대한 기수 정렬의 빅-오는 $O(ln)$ 이다. 이는 $O(n)$ 이다.

윤여준

Junior Backend Engineer