오늘 포스팅할 3번째 키워드로 공부하는 데이터 분석의 키워드는 Gaussian Distribution(정규분포)입니다.
Gaussian Distribution
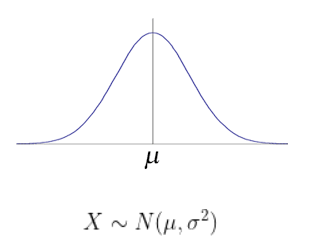
- 사진 출처 : 엣지있는 인공지능 : 정규분포
정규분포는 연속 확률 분포 중 하나로, 평균이 를 따르고, 분산이 을 따르는 분포이다.
데이터 분석에서 정규분포가 중요한 이유
표본이 크기가 커질 경우 중심극한 정리(CLT : Central Limit Theorem)에 따라 표본이 충분히 큰 경우, 정규분포를 따르게 되어 있습니다.
데이터 분석에서 정규분포를 하지 않는 변수들의 경우에도 Scaling, 로그변환 등을 통해 정규분포에 근사하도록 유도하여 학습을 시키기도 합니다.
마지막으로 인공지능에서 학습 데이터로 모델에 학습을 시킬 때, 모델의 기본 가정중에 정규분포를 가정사항으로 정하는 경우도 있으므로, 정규분포에 근사하여 학습을 진행해야 학습률을 높일 수 있습니다.
정규분포의 성질
-
정규분포에서의 기댓값, 최빈값, 중앙값 모두 이다.
-
평균과 표준편차가 주어져 있을 때, 엔트로피를 최대화 하는 분포이다.
-
정규분포곡선은 좌우 대칭이며, 하나의 꼭지를 가진다.
정규분포의 확률밀도함수(pdf)
정규분포 Maximum Likelihood Estimation
1. 분산을 알지만 평균을 모를 경우,
( 로 알려져 있지만, 는 알려져 있지 않은 경우)
2. 평균이 알려져 있고, 분산을 모르는 상태
3. 평균과 분산 둘 다 모르는 상태
데이터 분석에서 Gaussian Distribution 활용 사례
Anomaly Detection : 이상치 탐지
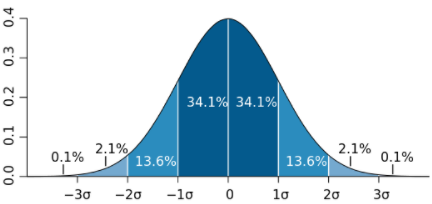
정규분포에서 평균에서 양쪽으로 n표준편차의 범위를 벗어나는 값들을 제거하는 방법을 n-sigma라고 한다.
예시로, 3-sigma는 평균에서 양쪽으로 3표준편차의 범위를 벗어나는 값을 탐지하는 이상치 탐지 방법을 3sigma법이라고 합니다.
Feature Scaling : Standard Scaler
정규분포 중 평균이 0, 분산이 1인 정규분포를 표준정규분포(standard normal distribution)이라고 합니다.
Feature Scaling이란 Feature들의 크기와 범위를 표준화 혹은 정규화 해주는 것을 의미합니다.
표준화
Standard Scaling은 Feature들의 크기와 범위를 표준화를 해줌으로 써, 표준정규분포를 가진 값으로 변환해줍니다.
Batch Normalization
Batch Normalization(배치 정규화)는 지난 포스트 Gradient Vanishing : 기울기 소실에서도 다뤘듯, 기울기 소실 문제를 해결하기 위해 배치 단위로 입력에 대해 평균을 0으로 만들고, 정규화를 합니다.
이 과정에서, 각 미니 배치들이 표준 정규분포를 따르도록 강제하여, Local Optimum 문제에 빠지는 가능성을 줄이고, Global Optimum 지점을 찾도록 도와줍니다.
Machine Learning Model Normality Assumption : 머신러닝 모델 정규분포 가정
선형회귀분석 가정 : 정규성
잔차항이 정규분포의 형태를 띄어야 한다.
선형 판별 분석(LDA: Linear Discriminant Analysis)
각 클래스 집단이 정규분포의 형태의 확률 분포를 가진다고 가정한다.
Gaussian Naive Bayes
연속적인 값을 지닌 데이터를 처리할 때, 각 클래스의 연속적인 값들이 정규분포를 따른다고 가정한다.
ARIMA
잔차항이 정규분포를 가져야 한다.
이 외에도 모수검정은 모집단이 정규분포임을 가정합니다..
+Gaussian이라는 단어가 들어가는 모델로는 Gaussian Process, SVM Gaussian Kernel 등이 있습니다.
Gaussian Mixture Model
Guassian Distribution에 대해 알아보고, 데이터 분석에서 이상치 탐지, 피쳐 스케일링, 정규성 가정이 있는 머신러닝 모델과 Gaussian이라는 이름이 들어가는 모델들도 알아보았습니다.
오늘 포스팅은 마지막으로 Gaussian Mixture Model에 대해 설명하고 마치도록 하겠습니다. Gaussian Mixture Model을 설명하기 앞서서, Maximum Likelihood Estimation(MLE)과 EM 알고리즘에 대한 이해가 있어야 하므로, MLE와 EM 알고리즘부터 대해 먼저 포스팅하도록 하겠습니다.
Maximum Likelihood Estimation(MLE)
Maximum Likelihood Estimation(최대우도법)은 모수적인 데이터 밀도 추정방법으로써 파라미터 로 구성된 어떤 확률밀도함수 에서 관측된 표본 데이터 집합을 이라 할 때, 이 표본들에서 파라미터 을 추정하는 방법입니다.
여기서, Likelihood는 지금 얻은 데이터가 어떠한 분포로 나왔을 가능도를 의미하며, 수치적으로 이 가능도를 계산하기 위해서 각 데이터 샘플에서 후보 분포에 대한 높이(즉, likelihood 기여도)를 계산하여 다 곱합니다.
likelihood function
likelihood 기여도를 다 곱해서 계산하는 것보다 log의 성질을 이용하면, 전부 더해서 계산할 수 있으므로, 계산의 편의를 위해 자연로그를 이용해 log-likelihood function을 만들어 줍니다.
log-likelihood
이제, 찾고자 하는 파라미터 에 대하여 편미분하고 그 값이 0이 되도록 하는 를 찾아 MLE를 구합니다.
EM algorithm
EM algorithm은 Expectation-Maximization의 약자로, log-likelihood의 기댓값을 계산하는 과정과 MLE를 수행해서 모수를 추정하는 과정으로 나눌 수 있습니다.
편의상 모집단을 구성하는 각 집단의 분포는 정규분포를 따른다고 가정한다. 각 자료가 어느 집단(클래스)으로부터 나온 것인지를 안다면 해당 모수의 추정이 어렵지 않을 것이다.
그러나 모집단으로부터 각 데이터가 어느 집단(클래스)으로부터 나온 것인지를 모르므로, 이 정보만을 자료로부터 추정할 수 있다면 최대가능도 추정의 문제는 쉽게 해결될 것이다. 따라서 각 자료가 어느 집단에 속하는지에 대한 정보를 가지는 잠재변수(latent variable)를 도입한다.
E-단계
잠재변수를 라 할 때, 모수에 대한 초기값이 주어져 있다면 (즉, 초기 분포를 안다면) 각 자료가 어느 집단으로부터 나올 확률이 높은지에 대해 추정이 가능하다.
만약 집단이 2개이고, 모든 자료에 대해 1집단에 속할 확률이 극단적으로 0 또는 1로만 추정되었다면, 이는 각 자료가 어느 집단에 속하는지를 아는 것과 마찬가지이므로 모수에 대한 추정이 쉽게 이루어진다. 즉, 각 자료에 대해 Z의 조건부분포(어느 집단에 속할 지에 대한)로부터 조건부 기댓값을 구할 수 있다. (임의의 파라미터 값을 정하고 Z 기대치 계산)
M-단계
관측변수 와 잠재변수 를 포함하는 에 대한 log-likelihood function(이를 보정된(augmented) log-likelihood function라 함)에 대신 상수값인 의 조건부 기댓값을 대입하면, log-likelihood function를 최대로 하는 모수를 쉽게 찾을 수 있다.
Z 대신 상수값인 Z의 조건부 기댓값을 대입하면, log-likelihood function를 최대로 하는 모수를 쉽게 찾을 수 있다. 갱신된 모수 추정치에 대해 위 과정을 반복한다면 수렴하는 값을 얻게 되고, 이는 MLE로 사용될 수 있다. (Z의 기대치를 이용하여 파라미터 추정 후, if likelihood == max -> 파라미터추정값 도출, else: -> 추정된 파라미터를 토대로 다시 Z 기대치 계산) => 이 과정의 횟수를 L(반복 횟수)로 표현
참고하기 좋은 자료 : 공돌이의 수학정리노트 : GMM과 EM 알고리즘
Gaussian Mixture Model
Gaussian Mixture Model은 데이터 셋들이 정규분포를 이룰 것이라고 가정하고, 데이터의 라벨이 주어져 있지 않을 때, likelihood 비교로 라벨링 후, 각 그룹별 모수를 추정한 뒤, 추정된 모수가 MLE인지 아닌지 확인하고, 파라미터 추정값을 도출하는 모델입니다.
여기서, Mixed Model은 전체 분포에서 하위 분포가 존재한다고 보는 모델입니다.
즉, 한 개의 분포가 아니라 여러 개의 분포로부터 생성되었다고 보는 것입니다. (Gaussian Mixture Model은 여러 개의 분포가 정규분포로 부터 생성되었다고 봅니다.
Gaussian Mixture Model(GMM : 가우시안 혼합 모델)은 샘플이 파라미터가 알려지지 않은 여러 개의 혼합된 정규분포에서 생성되었다고 가정하는 확률 모델입니다.
Gaussian Mixture Model(GMM)은 generative model 생성 모델입니다. 생성 모델은 학습 데이터를 학습하여 학습 데이터를 따르는 유사한 데이터를 생성하는 모델입니다.
Gaussian Mixture Model(GMM) 실습
Scikit-Learn의 make_moons 데이터를 통해 GaussianMixture 실습을 진행해보도록 하겠습니다. make_moons 함수는 초승달 모양 클러스터 두 개 형상의 데이터를 생성합니다. make_moons 명령으로 만든 데이터는 직선을 사용하여 분류할 수 없습니다.
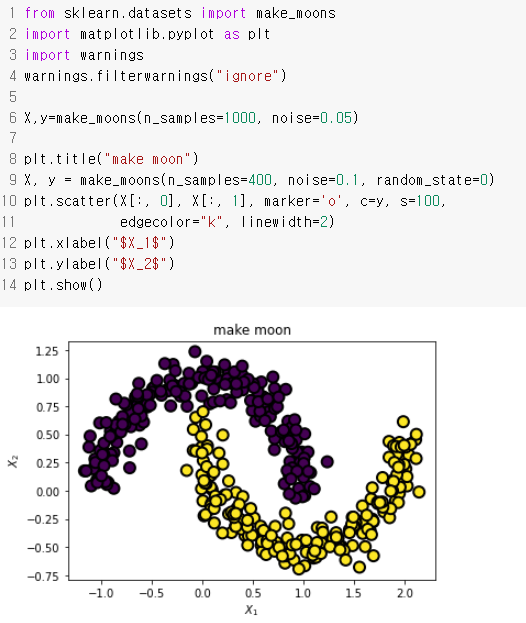
Scikit-Learn의 GaussainMixture 클래스로 기댓값-최대화 알고리즘(EM 알고리즘)이 추정한 파라미터를 확인 합니다.

GMM에서 score_samples() 메서드를 사용하여, 해당 위치의 확률 밀도 함수(PDF)의 로그를 예측합니다. 점수가 높을 수록 밀도가 높습니다.
input: print(f"gm.score_samples(X) \n {gm.score_samples(X)}")
output: gm.score_samples(X)
[-0.82889604 -1.07601095 -0.5781479 -1.62691711 -1.99954932 -1.68610971
-0.71876098 -1.9475925 -1.09975276 -1.93872469 -1.80938555 -0.86157821
-1.22472379 -0.56635783 -1.45547825 -2.18586591 -2.14784367 -0.41848486...
이하 생략Gaussian Mixture Model을 사용하여 이상치도 탐지할 수 있습니다.
Confusion Matrix(혼동 행렬)
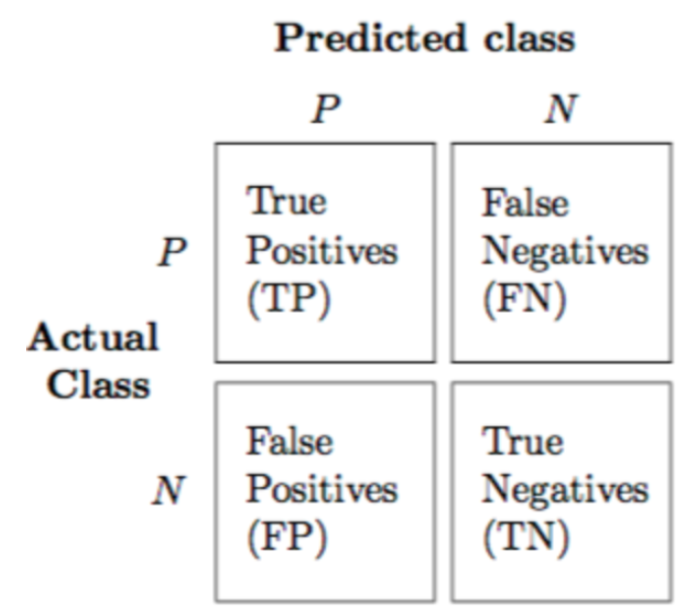
다음과 같이 Confusion Matrix(혼동 행렬)이 있다고 할 때,

정밀도와 재현율은 서로 트레이드 오프 관계입니다.
이를 해결하기 위해, threshold를 수정하여, imbalance target을 탐지하는데, 이 때도 Gaussian Mixture를 활용할 수 있습니다.
densities=gm.score_samples(X)
density_thresold=np.percentile(densities, 4)
anomalies=X[densities<density_thresold]
plt.figure(figsize=(8, 4))
plot_gaussian_mixture(gm, X)
plt.scatter(anomalies[:, 0], anomalies[:, 1], color='r', marker='*')
plt.ylim(top=5.1)
print("mixture_anomaly_detection_plot")
plt.show()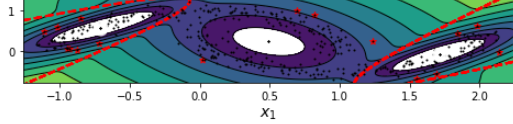
- 이상치를 빨간 점으로 표시하였습니다.
Gaussian Mixture Model 클러스터 개수 선택
BIC(Bayesian Information Criterion)이나 AIC(Akaike Information Critertion)을 최소화 하는 모델을 찾습니다. (AIC와 BIC는 향후 변수선택법 포스팅에서 자세히 다루도록 하겠습니다. AIC와 BIC는 낮을수록 좋은 모델이라는 의미입니다.)
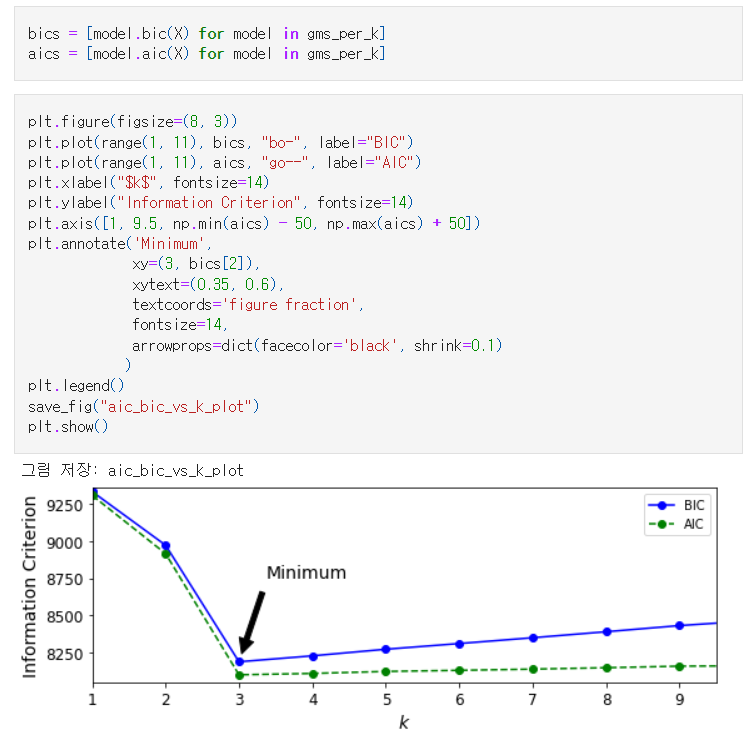
비지도학습에서 K-means 클러스터링에서 K를 결정할 때, 사용하는 Elbow Method처럼
가우시안 혼합 분포 모델에서는 BIC와 AIC가 가장 작아 질때의 클러스터 개수를 찾습니다.
Gaussian Mixture Model 중에 최적의 클러스터 개수를 수동으로 찾지 않는 BayesianGaussianMixture 클래스도 있으나, 이는 다음에 Bayesian에 대한 내용을 포스팅할 때 다루도록 하겠습니다.
GMM 실습은 핸즈온 머신러닝 책을 기반으로 하였으며, 실습에 대한 내용을 더 자세히 보고 싶으시면, handson-ml2/09_unsupervised_learning.ipynb를 참고해보셔도 좋을 듯 합니다.👍
마치며
오늘 포스팅에서는 정규분포에 대한 설명부터 데이터분석에서 정규분포가 활용되는 사례까지 알아보았습니다. 특히, 마지막엔 Gaussian Mixed Model에 대한 설명부터 실습까지 구체적으로 다루어보았습니다. 쓰다보니까 GMM 특집이 되어버린 것 같지만, 결국 핵심은 데이터 분석에서 빼먹을 수 없는 키워드중 하나가 "정규분포(Gaussian Distribution)"라는 것입니다. 이상으로 포스팅 마치도록 하겠습니다.😊"
