자료구조

데이터 유형은 수행해야할 연산을 기준으로 정한다

추상 데이터 : 데이터를 취급하기 위한 명세

• 특정 데이터 유형에 필요한 연산이 무엇인지 정해둔 명세이다.
• 데이터 변수를 조장하기 위한 인터페이스를 정의해둠으로써, 메모리 속에서 설제로 데이터를 저장하고 연산하는데 필요한 세부사항을 감출 수 있다.
• 추상 데이터 유형의 프로시저를 사용해 메모리를 직적 조작하지 않아도 된다.

추상 데이터 종류

1. 기본 데이터 유형
   프그래밍 언어에 내장되어 있어 외 모듈을 불러오지 않고도 쓸 수 있는 것

2. 스택(LIFO)

   • push(e) : 새 항목 e를 스택의 가장 위에 추가한다.
   • pop() : 스택의 가장 위의 항목을 가져오고 그 항목을 스택에서 제거한다.

3. 큐(FIFO)

   • engueue(e) : 새 항목을 e를 큐의 가장 뒤에 추가한다.
   • dequeue() : 큐의 가장 앞 항목을 가져오고 그 항목을 큐에서 제거한다.

4. 우선순위 큐

   • 큐와 비슷하지만 저장하는 항목의 우선순위를 부여할 수 있다.
   • enqueue(e,p) : 우선순위 수준 p에 따라 새 항목 e를 큐에 추가한다.
   • dequeue() : 큐의 가장 앞쪽 항목을 가져오고 그 항목을 큐에서 제거한다.

5. 리스트

   • 유연한 방식으로 데이터를 다루고 싶을때, 아무 위치에서나 항목을 추가, 제거 하고싶을 때 사용한다.
   • insert(n,e) : 항목 e를 n위치에 추가한다.
   • remove(n) : n 위치의 항목을 제거한다.
   • get(n) : n 위치의 항목을 구한다.
   • sort() : 리스트를 정렬한다.
   • slice(start,end) : start이상, end미만 사이 항목으로 리스트를 분리한다.
   • reverse() : 리스트의 순서를 거꾸로 한다.

6. 정렬 리스트

   • 리스트의 항목을 추가할 때마다 정렬을 해서 항상 정렬된 상태를 보장한다.
   • insert(e) : 항목 e를 올바른 위치에 추가한다.
   • remove(n) : n의 위치의 항목을 제거한다.
   • get(n) : n 위치의 항목을 구한다.

7. 맵(딕셔너리)

   • key와 value객체로 연관시켜 저장할 때 사용한다.
   • set(key,value) : 키-값 쌍을 추가한다.
   • delete(key) : key와 key에 연관된 값을 제거한다
   • get(key) : key에 연관된 값을 조회한다.

8. 집합

   • 항목의 순서가 무의미하거나 항목이 중복되지 않아야할 때 사용한다.
   • add(e) : 항목을 집합에 추가한다. 이미 존재하는 경우 오류가 발생한다.
   • list() : 집합의 항목을 나열한다.
   • delete(e) : 집합에서 항목을 하나 제거한다.

데이터 구조 : 데이터를 실제로 취급하는 방법

• 추상 데이터 유형은 어떤 데이터 유형에 지원되는 연산이 무엇인지만을 알려준다. 반대로 데이터 구조는 컴퓨터의 메모리 속에서 데이터가 실제로 구조화되는 방식과 그 데이터에 접근하는 방식을 알려준다.
• 동일한 추상 데이터 유형이라고 하더라도 여러가지 데이터 구조로 구현될 수 있다. 그러나 프로그램을 효율적으로 작성하려면 아무 모듈이나 쓰면 안된다.

1. 배열
   • 배열은 많은 수의 항목을 메모리에 저장할 때 사용할 수 있는 방법 중 가장 단순하고 기본적인 것이다.
   • 배열 속에 저장하려는 항목은 그 메모리 공간 속에 순차적으로 기록된다.
   • 마지막 항목 뒤에는 특별한 Null토큰을 기록하여 배열의 끝을 표시한다.
   • 배열에 저장된 각 객체는 메모리에서 동일한 용량을 차지한다.
   • 배열 속 어떤 항목이라도 '한번에'접근할 수 있다.
   • 스택을 구현하는데 특히 유용하지만, 리스트나 큐를 구현할 수도 있다.
   • 장점 : 프로그램이하기 쉽다. 접근 시간이 상수 시간이다.
   • 단점 : 크기가 큰 배열을 사용하려면 연속된 메모리 공간이 많이 필요하다. 배열 중간의 항목을 추가 제거하는 것이 까다롭다. 제거하고 모든 항목 한 칸씩 당기거나, 추가하고 밀어야하기 때문이다.

2. 연결 리스트
   • 항목을 저장한 칸들을 쇠사슬처럼 연결한 구조이다.
   • 배열과 달리 연속적인 메모리 주소로 구성될 필요가 없다.
   • 또 처음부터 필요한 모든 메모리를 할당해 둘 필요도 없다.
     그때그때 필요에 따라 할당하면 되기 때문이다.
   • 각 칸은 연결된 다음 칸의 주소를 가리키는 포인터를 갖는다.
   • 포인터가 비어있는 칸이 사슬이 끝나는 지점이다.
   • 연결 리스트로 스택, 큐, 리스트를 구현할 수 있다.
   • 장점 : 실행도중 리스트의 크기를 증가시켜도 문제가 되지 않는다. 언제나 남아있는 메모리 공간만큼 리스트를 만들 수 있다. 항목을 중간에 추가하거나 제거하는 것도 용의하다.
   • 단점 : 배열과 달리 n번째 항목을 상수시간에 가져오지 못한다. 첫 번째 칸부터 탐색을 시작해서 주소를 따라가야하기 때문이다. 한칸의 주소만 가지고 항목을 제거하거나 앞으로 옮길 수 없다. 각 칸은 다음 칸의 주소로만 가지고 있기 때문이다.

3. 이중 연결 리스트
   • 연결리스트에서 각 칸이 갖는 포인터를 두개로 늘려 이전 칸과 다음 칸의 주소를 가리키도록 한 것이다.(원형 연결 리스트도 가능)
   • 장점 : 연결 리스트의 장점을 그대로 계승한다.그리고 이전 칸의 포인터를 추가한 덕분에 한칸의 주소만으로도 그칸을 제거할 수 있다. 이전 칸의 포인터만 바꿔주면 되기 때문이다.
   • 단점 : n번째 항목에 상수 시간에 접근할 수 없다는 단점도 그대로다. 포인터가 두 개여서 데이터를 저장하는데 필요한 메모리가 더 많다.

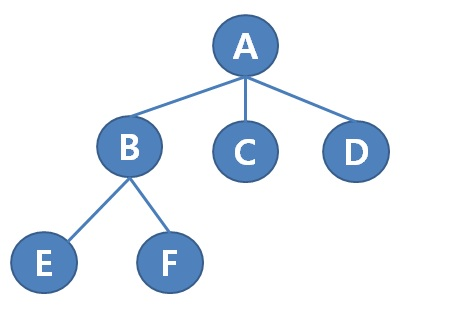
4. 트리

   • 트리도 연결리스트와 마찬가지로 메모리 칸을 이용해 정보를 저장한다.
   • 트리의 칸도 저장 대상 외에 다른 칸을 향한 포인터를 가진다.
   • 트리와 다른 점은 셀과 셀의 포인터가 한줄의 사슬로 연결된 것이 아니라 나무 형태의 구조로 연결된다는 것이다.
   • 트리는 파일, 디렉터리 구조나 군 명령계통 등의 계층 데이터에 적합하다.
   • 각 칸을 노드, 한 칸에서 다른 칸을 가리키는 포인터를 간선이라 한다.
   • 루트는 부모 노드를 갖지 않고, 나머지 노드는 모두 하나의 부모 노드를 갖는다.
   • 동일한 노드를 부모로 하는 노드는 자매 노드이다.
   • 한 노드에서 루트 노드까지의 경로 길이를 깊이(level)라고 한다.
   • 트리에서 가장 깊은 립(leap) 노드의 깊이가 트리의 높이가 된다.

5. 이진 탐색 트리

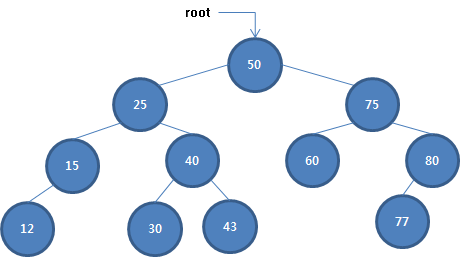
   • 이진 탐색 트리는 효율적인 탐색을 지원하는 특별한 트리이다.
   • 이진 탐색트리에서는 각 노드가 자식을 최대 두개만 가질 수 있다.
   • 노드의 위치는 키-값에 의해 결정된다. 부모 노드의 왼쪽 자식 노드는 부모 노드보다 키-값이 작아야하고, 오른쪽 자식 노드는 커야한다.
   • 이진 탐색 트리에 새 항목을 추가할 때는, 추가하려는 항목의 값을 트리에서 탐색해야한다. 탐색 과정에서 마지막으로 방문한 정점을 선택하여, 해당 정점의 왼쪽 또는 오른쪽 포인터로 새 정점을 가리키도록 해야한다.

6. 트리 균형 잡기

   • 이진 탐색 트리에 정점을 너무 많이 추가하면, 자식이 하나뿐인 정점이 많이 생기면서 트리의 높이가 너무 높아질 수 있다.
   • 이럴 때는 트리의 높이가 줄어들도록 정점을 재배열 해야한다.
   • 트리를 다루는 연산은 대부분 특정한 정점ㅂ에 다다를 때가지 정점의 연결을 따라 이동하는 과정을 피요로 하기 때문에 트리의 높이가 높을수록 경로가 길어져 특정 정보에 접근하기 위한 시간이 많이 소요된다.

• 트리 균형 잡기 예제
  • n개의 노드를 가진 이진 탐색 트리를 생각해보자.
  • 이 트리가 가질 수 있는 최대 높이는 n이며, 형태는 연결리스트와 같다.
  • 반대로 이트리가 가질 수 있는 최소 높이는 log2N이며, 이는 완전히 균형 잡핬을 때 가능하다.
  • 이진 탐색트리에서 항목을 탐색할 때 시간복잡도는 트리 높이에 비례한다.
  • 최악의 경우 n개의 항목을 가진 트리의 잎에 다다르는 경로를 모두 거치며 가장 깊은 곳 까지 탐색하는 시간 복잡도는 O(logN)dlek.
  • 그러나 트리의 균형을 잡으려면 모든 노드를 정렬해야해서 연산비용이 크다.
  • 따라서 항목이 추가, 제거 연산이 여러번 일어난 후에 균형을 잡는다.

• 자가 균형 이진 탐색 트리
  • 수정이 많이 발생하는 경우 자가 균형 이진탐색 트리를 활용한다.
  • 항목 추가, 제거 프로시저 그 자체에서 트리의 균형을 유지하는 트리이다.
  • 레드-블랙 트리 : 딕셔너리 구현에 자주 활용된다.
  • AVL트리 : 레드블랙트리보다 항목추가, 제거 시간이 더 걸리지만 균형을 잘잡아서 조회속도는 더 빠르다.
    읽기 작업이 높은 빈도로 일어나는 상황에 적합하다.
  • B-트리 : 노드 하나당 하나 이상의 항목을 저장할 수 있고, 자식도 둘 이상 연결할 수 있다. 따라서 큰 덩어리의 데이터를 효율적으로 처리할 수 있다.

7. 이진 힙

   • 각 노드에서 최대 또는 최소 항목을 즉시 발견할 수 있도록 정렬된 트리이다.
   • 우선순위 큐를 구현할 때 이 데이터 구조가 특히 유용하다.
   • 힙에서는 최대 또는 최소 항목을 구하는 비용이 O(1)이다.
     힙의 최대 또는 최소 항목이 항상 트리의 루트이기 때문이다.
   • 노드의 탐색 추가 비용은 여전히 O(logN)이다.
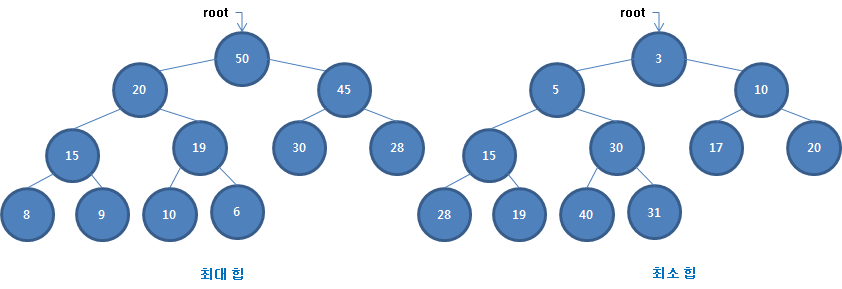
   • 이진 탐색 트리와 달리 힙에서는 노드들의 순서가 일정하지 않다.
     다만, 부모 노드는 자신의 두 자식 노드보다 반드시 크다.
     (최소 항목을 구하는 힙에서는 반드시 더 작다.)
   • 항목들 사이에 최댓값, 최솟값을 빈번하게 사용한다면 이진 힙을 사용한다.

8. 그래프

   • 트리와 비슷하지만 부모, 자식 노드가 없고 루트 노드도 없다.
   • 그래프에서 데이터가 노드와 간선으로 자유롭게 배열될 수 있다.
   • 모든 노드는 다른 노드를 가리키는 간선을 여러개 가질 수 있다.
   • 네트워크 관계, 연결망을 표현하기에 이상적이다.

9. 해시 테이블

   • 항목의 탐색 비용을 O(1)로 수행할 수 있는 데이터 구조다.
   • 전체 항목 수가 몇개든 비용이 상수시간으로 동일하다.
   • 해시 테이블을 사용하기 위해서는 연속적인 메모리를 미리 할당해야 한다.
     하지만 항목을 순차적으로 저장하지 않는다.
   • 해시 함수는 저장하려는 데이터를 입력받아 의미 없고 불규칙해보이는 수를 출려한다. 그리고 이렇게 나온 수가 항목을 젖아할 위치가 된다.
   • 해시 테이블에서 어떤 값을 조회할 땐, 먼저 그 값을 해시 함수에 입력하낟. 그럼 해시함수는 메모리속에 항목이 저장되어 있을 정확한 위치를 출력해준다.
   • 해시 충돌 : 가끔 해시 함수가 서로 다른 두 입력값에 대해 동일한 메모리 위치를 반환하는 것 ➡️ 동일한 메모리 주소에 연결 리스트로 저장하든가 한다. ➡️ 해시 충돌이 일어나면 CPU와 메모리의 추가비용이 발생한다.
   • 해시충돌을 방지하기 위해 해시 테이블 공간을 최소 50%는 남겨둬야 한다.
   • 해시 테이블은 딕셔너리와 집합을 구현하는데 자주 사용된다.
   • 항목을 추가, 제거가 트리 기반의 데이터 구조에 비해 빠르다.
     하지만 올바르게 동자하기 위해 대량의 연속적 메모리 공간이 필요하다는 단점이 있다.

참조

• https://chanyeong.com/blog