1. 개념
- 특정 원소(피벗, pivot)를 기준으로 주어진 배열을 두 부분배열로 분할하고, 각 부분배열에 대해서 퀵 정렬을 순환적으로 적용하는 알고리즘
- 피벗이 제자리를 잡도록 하여 정렬
왼쪽 부분배열의 모든 값 < 피벗 < 오른쪽 부분배열의 모든 값
2. 과정
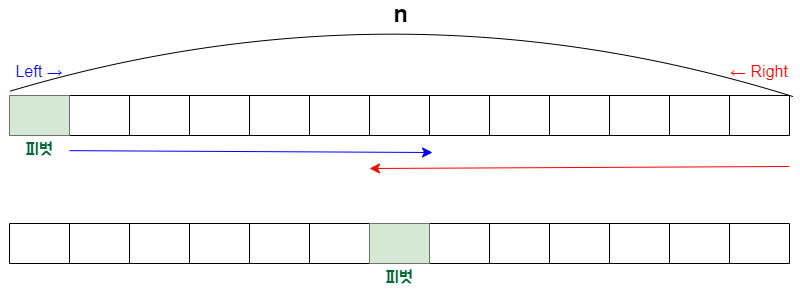
- 피벗 선정 : 배열 중 기준으로 삼을 원소 하나를 고른다.
- 분할 : 피벗을 기준으로 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 배열을 둘로 나눈다.
- 재귀 : 분할된 두 개의 작은 배열에 대해 위의 과정을 반복하여, 배열의 크기가 0이나 1이 될 때까지 반복하며 정렬한다.
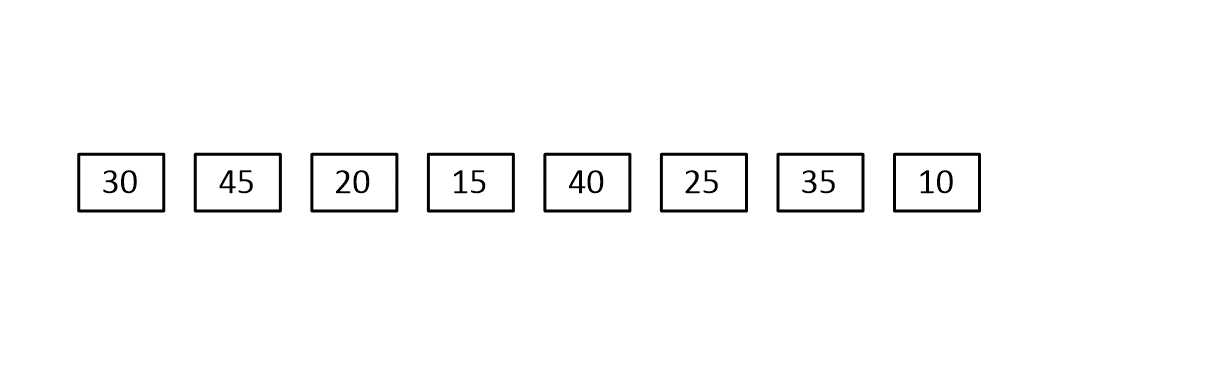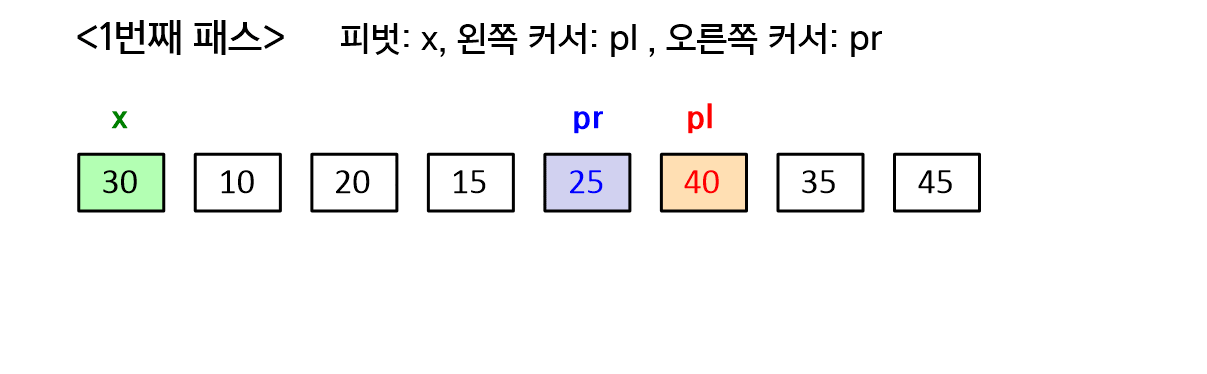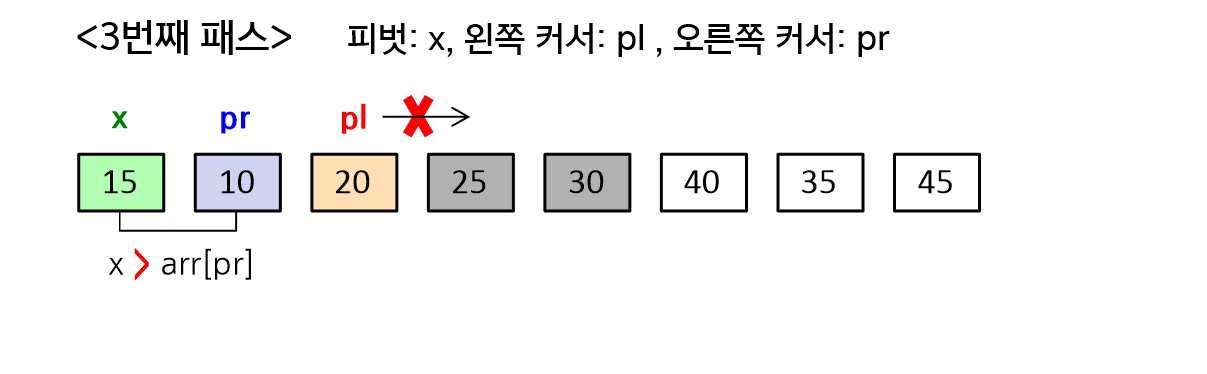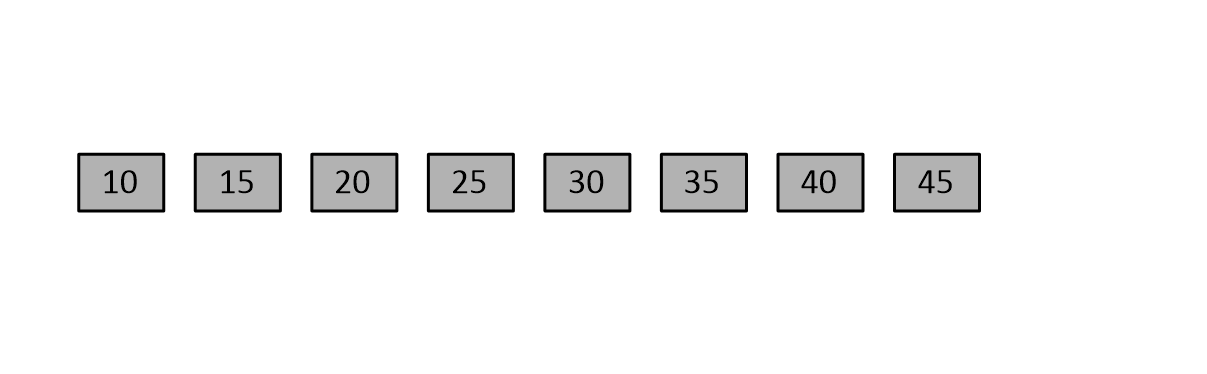
3. 구현
/* n: 배열의 길이 */
// 배열 값 교환
static void swap(int[] arr, int idx1, int idx2) {
int temp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = temp;
}
// 두 부분배열로 분할
static int partition(int[] arr, int left, int right) {
int x = arr[left]; // 피벗
int pl = left+1; // 왼쪽 커서
int pr = right; // 오른쪽 커서
// 1-1. 피벗 x를 기준으로 배열 arr 분할
while (pl <= pr){
// 피벗 x보다 큰 값의 위치 찾기
while (pl <= right && arr[pl] < x) {
pl++;
}
// 피벗 x보다 작은 값의 위치 찾기
while (pr >= left+1 && arr[pr] > x) {
pr--;
}
if (pl <= pr) {
swap(arr, pl++, pr--); // arr[pl]과 arr[pr] 교환
}
}
// 1-2. 피벗 위치 조정
swap(arr, left, pr);
return pr; // 피벗 위치 반환
}
static void quickSort(int[] arr, int left, int right) {
if(left < right) {
int x = partition(arr, left, right); // 1. 배열 분할 후 피벗 위치 얻음
quickSort(arr, left, x-1); // 2. 왼쪽 부분배열에 대한 순환 호출
quickSort(arr, x+1, right); // 3. 오른쪽 부분배열에 대한 순환 호출
}
}1. partition() 메소드를 실행하여 배열을 두 부분배열로 분할하고 피벗 위치를 얻어온다. 피벗은 현재 배열의 맨 처음 요소로 지정한다(x = arr[left]). 피벗을 제외한 나머지 부분을 정렬하기 위해 피벗의 다음 요소를 왼쪽 커서로(arr[left+1]), 배열의 맨 마지막 요소를 오른쪽 커서로(arr[right]) 지정한다.
1-1. 왼쪽 커서는 피벗(이하 x)보다 큰 값을 찾을 때까지 오른쪽으로 이동하고(pl++), 오른쪽 커서는 x보다 작은 값을 찾을 때까지 왼쪽으로 이동한다(pl--). x를 기준으로 왼쪽은 보다 작은 값, 오른쪽은 x보다 큰 값이 와야하므로, 방금 찾은 두 값(arr[pl], arr[pr])의 위치를 조정해줘야 한다. 왼쪽 커서와 오른쪽 커서의 위치가 x를 기준으로 교차하지 않은 상태라면(pl <= pr), arr[pl]와 arr[pr]를 서로 교환해준다. 이 과정은 왼쪽 커서와 오른쪽 커서의 위치가 교차하지 않는 동안 반복한다.
1-2. 왼쪽 커서와 오른쪽 커서의 위치가 x를 기준으로 교차한 상태라면(pl > pr), 현재 피벗(arr[left])과 오른쪽 커서의 값(arr[pr])을 교환해주어 피벗을 알맞은 위치로 이동시켜주고, 오른쪽 커서의 값은 배열의 맨 앞으로 이동하여 다음 피벗으로 사용할 수 있도록 한다. 이 과정이 끝나면, 현재 피벗의 위치를 반환한다.
2. 얻어온 피벗의 위치를 기준으로 배열의 크기가 0이나 1이 될때까지 왼쪽 배열을 과정 1을 반복하여 정렬한다. 왼쪽 배열의 범위는 원래 배열의 맨 앞 요소(arr[0])부터 피벗의 바로 앞 요소(arr[x-1])까지이다.
3. 얻어온 피벗의 위치를 기준으로 배열의 크기가 0이나 1이 될때까지 오른쪽 배열을 과정 1을 반복하여 정렬한다. 오른쪽 배열의 범위는 피벗의 바로 다음 요소(arr[x+1] 분할된 오른쪽 배열의 마지막 요소(arr[right]) 까지이다.
4. 위의 모든 과정을 수행하면 정렬이 완료된다.
4. 성능 분석
4-1. 분할 함수(Partition()) 수행 시간
- 피벗과의 비교 횟수 =>
Θ(n)
4-2. 퀵 정렬(QuickSort()) 수행 시간
static void quickSort(int[] arr, int left, int right) {
if(left < right) {
int x = partition(arr, left, right); // T(n)
quickSort(arr, left, x-1); // T(left)
quickSort(arr, x+1, right); // T(right)
}
}
4-2-1. 최악(0:n-1, n-1:0) → O(n^2)
-
피벗만 제자리를 잡고 나머지 모든 원소가 하나의 부분배열이 되는 경우
-
피벗이 항상 부분배열의 최솟값 또는 최댓값이 되는 경우
-
입력데이터가 정렬된 상태 + 피벗을 배열의 처음 원소로 정한 경우
1020304050=>0 : n-11020304050=> 1:4 → 4
1020304050=> 2:3 → 3
1020304050=> 3:2 → 2
1020304050=> 4:1 → 1
1020304050
5040302010=>n-1 : 01040302050=> 4:1 → 4
1040302050=> 3:2 → 3
1020304050=> 2:3 → 2
1020304050=> 1:4 → 1
1020304050- (n-1) + (n-2) + (n-3) + ... + 1 = n(n-1)/2
- T(n) = T(n-1) + T(0) + Θ(n) (n>0), T(0)=0
T(n) = T(n-1) + Θ(n)
∴ 시간복잡도 O(n^2)
4-2-2. 최선/평균 → O(nlogn)
-
n/2:n/2
-
피벗을 중심으로 항상 동일한 크기의 두 부분배열로 분할되는 경우
-
피벗이 항상 부분배열의 중간값이 되는 경우
3045354020152520251530403545=> 4
15202530403545=> 2
15202530354045=> 2
15202530354045
T(n) = T(⌊n-2⌋) + T(⌊n-2⌋) + Θ(n) (n>1), T(1)=1
T(n) = 2T(n-2) + Θ(n)
∴ 시간복잡도 O(nlogn) -
-
피벗이 동일한 확률로 분할 후 배열의 어느 곳에나 위치하는 경우
- 0:n-1, 1:n-2, 2:n-3, ..., n/2:n/2, n-2:1, n-1:0
5. 특징
- 불안정적 정렬 알고리즘이다.
- 분할 정복 알고리즘이다.
- 피벗 선택의 임의성만 보장되면 평균 성능을 보일 가능성이 매우 높다.
- 배열에서 임의의 값을 선택한 후, 배열의 처음 원소와 서로 교환한 후 정렬을 수행하는 것이 좋다.
📖 참고
- Bohyoh Shibata. (2020). Do it! 자료구조와 함께 배우는 알고리즘 입문 - 자바편(강민 옮김). 이지스퍼블리싱
- 이관용. "알고리즘 3강. 분할정복 알고리즘 (1)" 방송통신대학교, 2022년.