자료구조와 함께 배우는 알고리즘 입문 [파이썬] - 9장. 트리

9-1. 트리구조

• 가장 위쪽 노드를 ‘root’, 가장 아래쪽 (가지가 더 이상 없는)노드를 ‘leaf’ (단말노드)라고 한다.
• 부모가 같은 노드는 형제노드
• 루트에서 얼마나 멀리 떨어져 있는지를 ‘레벨’
• 각 노드가 갖는 자식의 수를 ‘차수 degree’, 모든 노드의 차수가 n이하인 트리를 ‘n진 트리’
• 루트에서 가장 멀리 있는 리프까지의 거리를 ‘높이’
• 어떤 노드를 루트로 하고, 그 자손으로 구성된 트리를 ‘서브트리’
• 형제노드끼리 순서가 있으면 ‘순서 트리’ 없으면 ‘무순서 트리’

• 너비 우선 검색
  • 폭 우선 검색, 가로검색
  • 낮은 레벨부터 왼쪽에서 오른쪽으로 검색하고, 검색 마치면 다음 레벨로 내려감
• 깊이 우선 검색
  • 세로 검색, 수직 검색
  • 리프에 도달할 때까지 아래쪽으로 내려가면서 검색 리프에 도달하면 부모노드로 돌아감
    

• 전위순회 preorder
  - root - left - right
  - 루트노드 탐색 - 왼쪽 자식노드 탐색 - 오른쪽 자식노드 탐색하는 방식
  

# 전위순회
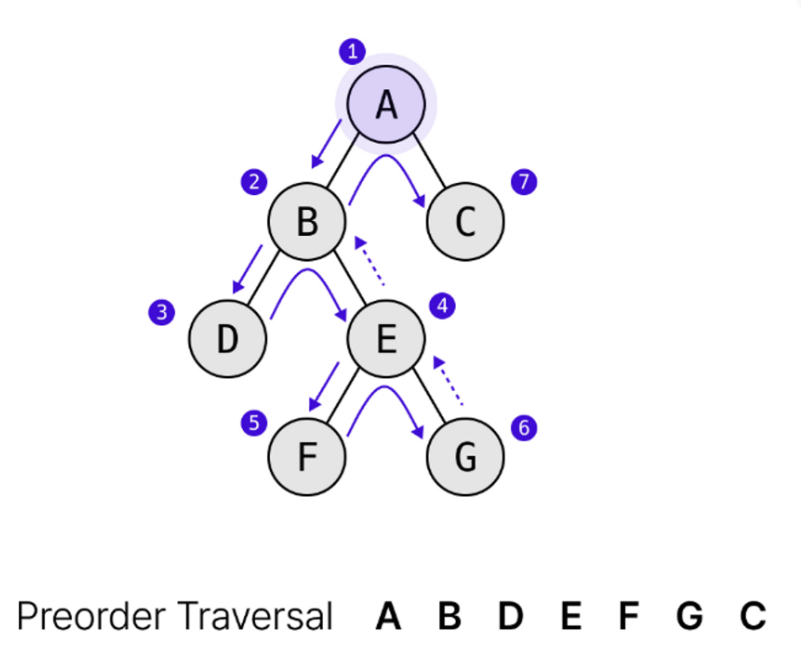
def preorder(i):
    if i:  # 존재하는 정점이면
        print(i, end=' ')
        preorder(left[i])
        preorder(right[i])
    return
    
"""
13
1 2/ 1 3/ 2 4/ 3 5/ 3 6/ 4 7/ 5 8/ 5 9/ 6 10/ 6 11/ 7 12/ 11 13/ 부모 자식/
"""
V = int(input())
arr = list(map(int, input().split()))
E = V - 1
left = [0] * (V+1)  # 부모를 인덱스로 왼쪽자식 저장
right = [0] * (V+1)  # 오른쪽자식 저장
par = [0] * (V+1)  # 자식을 인덱스로 부모 저장
# child = [[] for _ in range(V+1)]
for i in range(E):
    p, c = arr[i*2], arr[i*2+1]
    # 왼쪽노드에 값이 안들어가있으면 추가
    if left[p] == 0:
        left[p] = c
    # 왼쪽 다음 오른쪽 확인
    else:
        right[p] = c
    # 자식노드에 대해 부모 노드 값 저장
    par[c] = p
    # child[p].append(c)  이거랑 같음
root = 1
while par[root] != 0:  # root 찾기
    root += 1
preorder(root)
# 1 2 4 7 12 3 5 8 9 6 10 11 13
print()

• 중위순회 inorder
  - left - root - right
  - 왼쪽 자식노드 탐색 - 루트노드 탐색 - 오른쪽 자식노드 탐색하는 방식
  

#중위순회
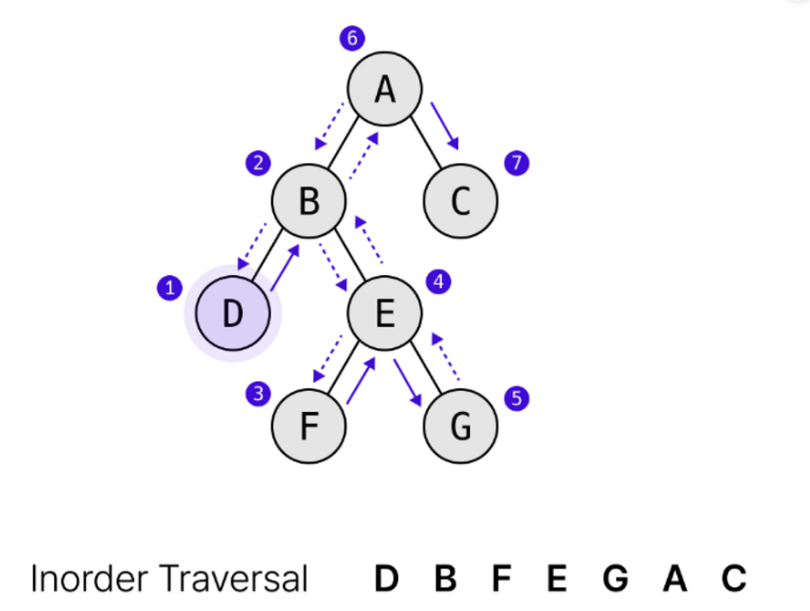
def inorder(i):
    if i:  # 존재하는 정점이면
        inorder(left[i])
        print(i, end=' ')
        inorder(right[i])
    return
    
"""
13
1 2/ 1 3/ 2 4/ 3 5/ 3 6/ 4 7/ 5 8/ 5 9/ 6 10/ 6 11/ 7 12/ 11 13/ 부모 자식/
"""
V = int(input())
arr = list(map(int, input().split()))
E = V - 1
left = [0] * (V+1)  # 부모를 인덱스로 왼쪽자식 저장
right = [0] * (V+1)  # 오른쪽자식 저장
par = [0] * (V+1)  # 자식을 인덱스로 부모 저장
# child = [[] for _ in range(V+1)]
for i in range(E):
    p, c = arr[i*2], arr[i*2+1]
    # 왼쪽노드에 값이 안들어가있으면 추가
    if left[p] == 0:
        left[p] = c
    # 왼쪽 다음 오른쪽 확인
    else:
        right[p] = c
    # 자식노드에 대해 부모 노드 값 저장
    par[c] = p
    # child[p].append(c)  이거랑 같음
root = 1
while par[root] != 0:  # root 찾기
    root += 1
inorder(root)
# 12 7 4 2 1 8 5 9 3 10 6 13 11
print()

• 후위순회 postorder
  - left - right - root
  - 왼쪽 자식노드 탐색 - 오른쪽 자식노드 탐색 - 루트노드 탐색하는 방식
  

# 후위순회
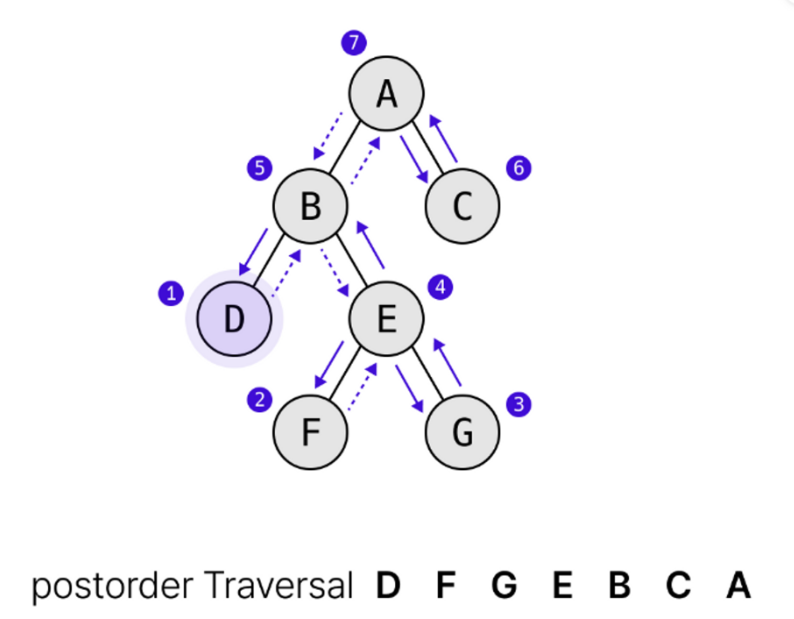
def postorder(i):
    if i:  # 존재하는 정점이면
        postorder(left[i])
        postorder(right[i])
        print(i, end=' ')
    return

"""
13
1 2/ 1 3/ 2 4/ 3 5/ 3 6/ 4 7/ 5 8/ 5 9/ 6 10/ 6 11/ 7 12/ 11 13/ 부모 자식/
"""
V = int(input())
arr = list(map(int, input().split()))
E = V - 1
left = [0] * (V+1)  # 부모를 인덱스로 왼쪽자식 저장
right = [0] * (V+1)  # 오른쪽자식 저장
par = [0] * (V+1)  # 자식을 인덱스로 부모 저장
# child = [[] for _ in range(V+1)]
for i in range(E):
    p, c = arr[i*2], arr[i*2+1]
    # 왼쪽노드에 값이 안들어가있으면 추가
    if left[p] == 0:
        left[p] = c
    # 왼쪽 다음 오른쪽 확인
    else:
        right[p] = c
    # 자식노드에 대해 부모 노드 값 저장
    par[c] = p
    # child[p].append(c)  이거랑 같음
root = 1
while par[root] != 0:  # root 찾기
    root += 1
postorder(root)
# 12 7 4 2 8 9 5 10 13 11 6 3 1
print()

---

9-2. 이진트리와 검색트리

• 이진트리 : 자식노드가 최대 두개인 트리
• 완전 이진 트리
  • 마지막 레벨을 제외하고 모든 레벨에 노드가 가득 차 있음
  • 같은 레벨에서 노드가 왼쪽부터 오른쪽으로 채워져 있음
  • 마지막 레벨은 왼쪽부터 노드를 채우되 끝까지 채워져있지 않아도 된다.
  • 높이가 k인 완전 이진 트리가 가질 수 있는 노드 최대 수는 $2^(k+1) - 1$
  • n개 노드 저장할 수 있는 트리 높이는 log n

• 균형 검색 트리
  • 노드가 일렬로 한쪽으로 쭉 이어진 트리
  • 이진의 균형 검색 트리: AVL트리, 레드블랙트리
  • 이진이 아닌 균형 검색 트리: B트리, 2-3트리

• 이진 검색 트리
  • 왼쪽 서브트리 노드의 키 값은 자신의 노드 키 값보다 작아야 한다.
  • 오른쪽 서브트리 노드의 키 값은 자신의 노드 키 값보다 커야 한다.
  • 키 값이 같은 노드는 존재하지 않는다

• 구조 단순, 노드 삽입하기 쉬움
• 중위 순회의 깊이 우선 검색을 하면 노드값을 오름차순으로 얻을 수 있다