🌈 시작하며

이 문제 정말 재밌어요.
저는 개인적으로 이 문제가 요근래 푼 문제 중 가장 우아하다고 생각했습니다.

정답률이 꽤 낮아서, 이번에 몸이 아파서 개발을 잠시 쉬는 와중에 한 번 풀어봤는데, 푸는 시간 내내 시간 가는 줄 몰랐답니다 🙃

그렇다면, 어떻게 풀었는지 살펴볼까요?

🚦 본론

상황 가정

저는 요새 문제를 풀 때 저만의 문제를 구현해야 하는 상황을 가정하고 푸는 연습을 합니다.
이유는, 결국 알고리즘을 공부하며 우리가 달성하고자 하는 것은, 이런 문제가 생기면 어떻게 풀 것인가를 익히는 것이라고 생각했습니다.

이를 확장하면, 결국 문제를 해결하기 위한 구현 방식을 어떻게 설계할 것인가 역시 거시적인 관점에서 알고리즘 해결 과정에 포함된다고 생각합니다.

따라서 문제에 주어진 상황과 더불어 오버엔지니어링을 허락하는 상황을 가정해보기로 했어요.

주어진 상황

• 행렬에 대한 계산 솔루션을 구현해야 한다.
• 이 행렬 계산기는 현재 앞으로도 구현할 사항이 많아질 것으로 예상하여, 초기부터 잘 설계해야 하기로 팀 간에 합의가 되었다.
• 행렬의 출력 방법은 클라이언트의 요구에 따라 앞으로도 다양해질 수 있다.

어차피 몸이 아파서 더이상 공부도 못하겠고, 시간도 많겠다! 😆
문제를 푸는 데 추가 상황까지 생각하니 정말 재밌었어요.

🚨 이 문제 해결과정은 주어진 배경 자체가 남들이 보기에 오버엔지니어링스러운 답이 나오겠다는 느낌이 들 거에요. 대신 이해하기 쉽게끔 자세하게 풀이로 서술해볼게요! 🙆🏻

시간복잡도

사실 이 문제를 봤을 때부터 어떻게 풀지는 금방 느낌이 왔어요.
대충 N = 100000(행렬의 총 행/렬 셀 개수)인데, 연산이 100000개라니!
(여기서부터 눈치를 채셔야 합니다. 2차원 배열을 업데이트하며 푸는 건 안 되겠다는 걸 말이죠.)

일단 대충 O(NlogN)이어야 풀 수 있을 거 같은데, 일반적인 로직으로는 연산을 처리하는 도중에 끝나버릴 것 같다는 생각이 들었어요.

즉, 이건 최적화를 위한 고민을 잘 해야 하는 문제라는 것을 단번에 직감했습니다.

따라서 다음과 같은 가정을 했습니다.

• Rotate를 하면 어떻게 바뀌는 걸까?
• ShiftRow를 하면 어떻게 바뀌는 걸까?

핵심은, 이 메서드를 어떻게 최적화하는지라는 것을 알 수 있는 대목입니다.

메서드 분석

Rotate

우리가 하나의 객체를 만들게 되고, 여기에는 Rotate, ShiftRow라는 2개의 연산을 관장한다고 생각해봅시다.

그렇다면, Rotate는 어떻게 매트릭스가 바뀔까요?

가령 이런 배열이 있다고 상상해봅시다.

이 배열이 Rotate하면 어떻게 될까요?

이런 식으로 바뀌게 될 것입니다.
그런데 생각해보자구요.

이 연산을 1000번 했을 때, 검은색 부분이 바뀔 가능성이 있을까요?

절대 없을 겁니다.
즉, 우리는 Rotate 여러 번 할 때, 이를 해당 분홍색 구간만 제어하면 된다는 이야기입니다.

일단 이정도의 영감만 얻고, 다음 메서드를 살펴보죠!

ShiftRow

연속으로 위의 변화한 배열에서 ShiftRow를 한다고 생각해봅시다.
기존의 다음과 같은 배열은

이렇게 변하게 될 것입니다.
이중, 가장 두드러진 특징은 맨 아래쪽이 윗쪽으로 이동한다는 것인데요.
사실 이 메서드는 모든 셀을 변화시키는데요. 가장 두드러진 특징은 맨 아래의 줄이 삭제되고, 맨 앞에 넣어진다는 것입니다. 이는 Deque의 특징과 같군요?!

따라서 덱의 느낌을 잘 주는 가장 관련된 부분을 녹색으로 표시했습니다.

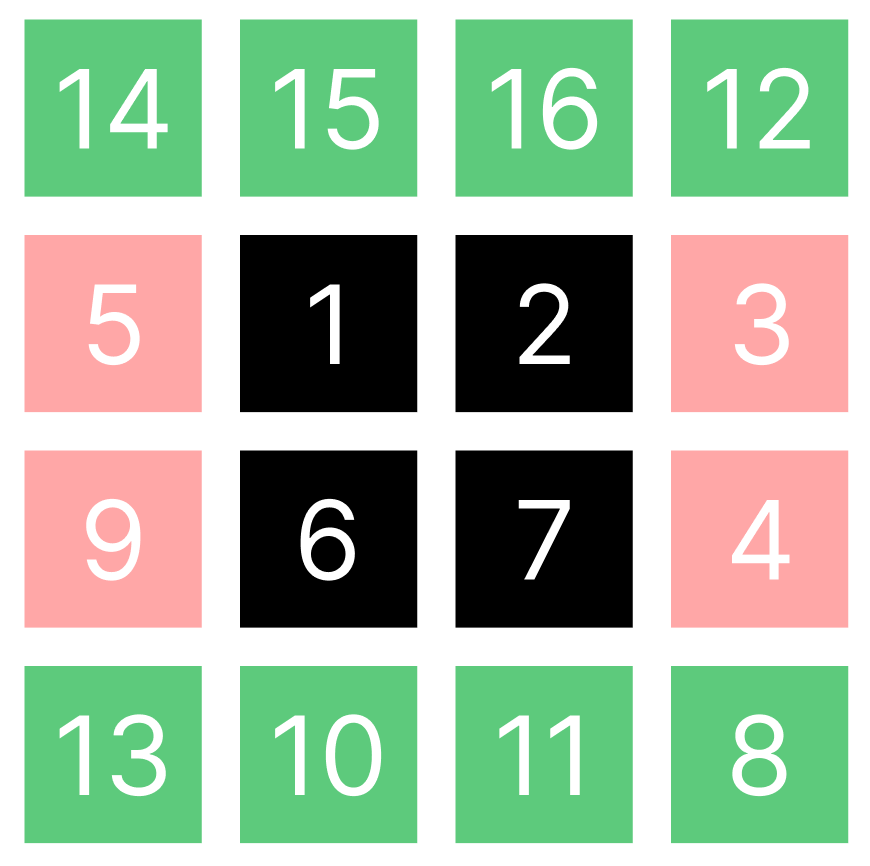
그래서 하고 싶은 말이 무엇인가요? 😖

어찌 보면 여기까지 봤을 때, 쉽게 설계에 접근하지 못할 수 있습니다.
왜냐구요? 일반적인 인지사고로는 자연스럽게 주어진 문제가 행렬이라는 측면에서 직관적으로 2차원 배열을 떠올리기 때문입니다.

하지만 다르게 보면 어떨까요?
비슷한 것들끼리 한 번 묶는 방법 중에는, 다음과 같이 묶을 수 있을 것 같아요.

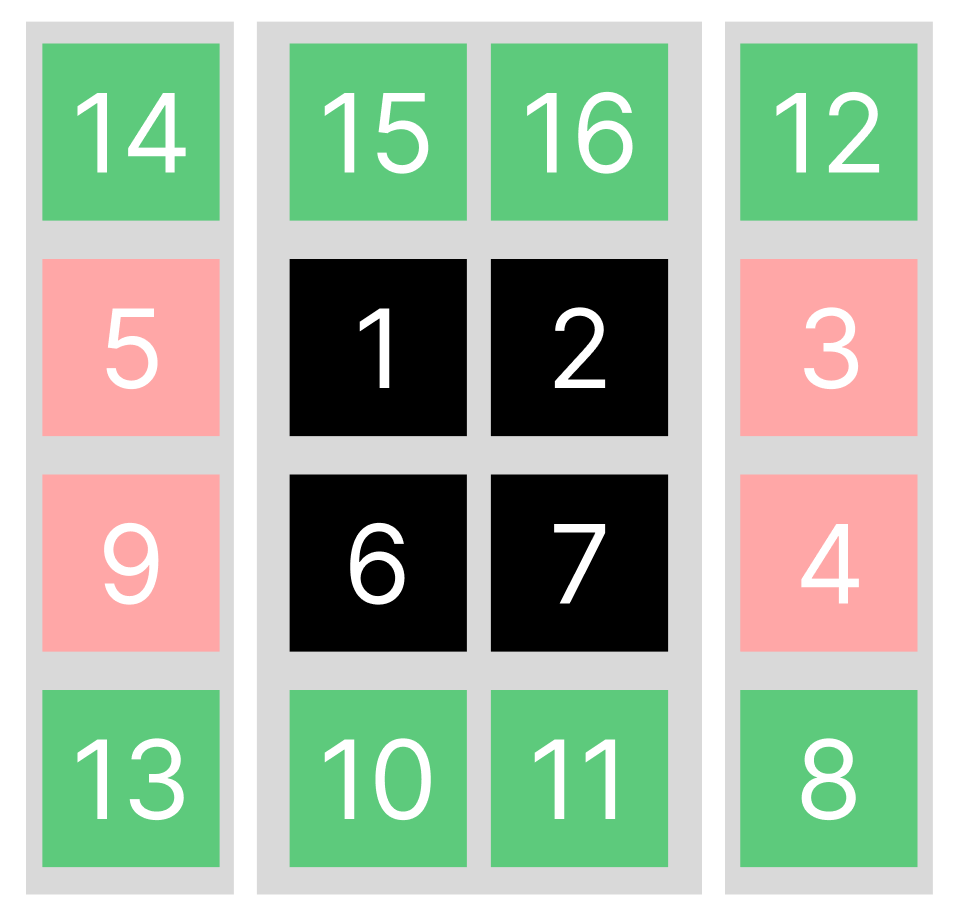
엇... 뭔가 느낌이 들지 않나요?
위/아래 줄 값에서 삽입/삭제가 이루어지는 뭔가 특이한 자료구조가 3개가 탄생했군요!

우선 이 분류된 3개의 그룹을 다음과 같이 정의하겠습니다.

• 왼쪽 그룹: Left
• 중앙 그룹: Main
• 오른쪽 그룹: Right

Left

자. 그러면 이 Left는 Rotate할 때에는 다음과 같이 되겠군요.

• Rotate할 때 맨 윗쪽이 Main의 맨 첫번째 줄 앞으로 빠져나가겠네요.
• Rotate할 때 맨 아랫쪽에서는 Main의 맨 아랫 줄 맨 앞의 것이 들어오겠네요.
• ShiftRow할 때 자체적으로 맨 아랫 것이 맨 윗쪽으로 가겠네요.

어? 그렇다면, ShiftRow를 효율적으로 구현하기 위해 Deque의 자료구조로 구현하면 어떨까요?

그럼 결과적으로 O(1)만큼의 삽입과 삭제가 이루어지므로 연산을 최적화할 수 있겠군요!

Main

그렇다면 Main도 따져보자구요. (Main의 경우 좀 어려울 수 있어요! 🙇🏻‍♂️)
Main의 경우는 한 줄에 또 여러 개의 값을 갖고 있음에 주의하면서 봅시다.

• Rotate할 때 맨 윗쪽에서는 Left의 맨 앞이 들어오겠네요.
• Rotate할 때 맨 마지막 값은Right의 맨 앞으로 빠져나가겠네요
• Rotate할 때 맨 아랫쪽의 맨 뒷쪽 값으로 Right의 맨 뒤의 값이 들어오겠네요.
• Rotate할 때 맨 아랫쪽의 맨 앞쪽 값이 Left의 맨 아랫쪽 값으로 빠져나가겠네요.
• ShiftRow할 때 자체적으로 맨 아랫 것이 맨 윗쪽으로 가겠네요.

결과적으로 Main의 각 줄 역시 Rotate를 할 때 삽입, 삭제가 양쪽 모두 이루어져야 합니다. (shiftRow하다 보면 언제 맨 위/아래가 될지 모르기 때문이죠)
따라서 Main의 각 row는 Deque로 구현하면 되겠네요.

그렇다면 Main 자체는 어떨까요?
이 역시 ShiftRow할 때, 맨 앞쪽을 삽입해야 하므로 Deque로 구현해야 합니다.
즉, Main은 Deque[Deque[]]의 2차원으로 이루어진 덱 구조겠네요.

Right

마지막으로 Right 역시 Left와 마찬가지의 형태를 띄고 있죠?
따라서 Deque로 이루어진 자료구조로 쉽게 두 연산을 최적화할 수 있어요.

끝이 아니다! 커맨드 최적화가 가능하다!

그런데 말이죠. 커맨드를 압축시킨다면 어떨까요?

예컨대, shiftRow는 총 행렬의 Row개만큼 적용하면 원래의 행렬 상태로 돌아옵니다. 또한, rotate 역시 테두리만큼 연산이 적용되면 원래의 행렬 상태로 돌아오죠.

즉, 최적화할 수 있는 부분이 존재하지요!

중간 정리! - 연산 최적화를 위한 자료구조 선택

결과적으로 우리는 연산 최적화를 할 수 있는 방법을 찾아냈어요.
그것도 우아하게, 자료구조를 잘 선택하는 것만으로요. 😉

1. 행렬이 아닌, 2차원 배열을 3개의 덱으로 분할하고 연산마다 로직에 맞게 적용한다.
2. 이는 각 연산이 덱을 통해 이루어지므로 O(1)의 시간복잡도로 연산을 해결한다.
3. 모든 커맨드들을 똑같은 것들끼리 압축함으로써 최적화가 가능하다.

코드 구현 과정

🚨 여기는 앞서 말한, 저 나름대로의 문제를 가정하고 해결하면서 나온 오버 엔지니어링 구간입니다.
만약 단순히 답을 참고하고 싶다면 맨 아랫 쪽의 <결과 코드>로 이동해주세요.

따라서 이제는 로직을 설계해야 해요.
어떻게 하면 이 문제를 부분적으로 잘 나누고, 객체 지향적인 설계로 해결할 수 있을까요?

세부 구현 - 내부 클래스 시스템의 전체적인 동작을 핸들링하는 MatrixCalculator

저는 일단 이 문제를 바라봤을 때, 퍼사드 패턴으로 큰 객체를 만드는 게 가장 바람직하다고 생각했습니다.

이유는, 모든 서브 클래스 시스템들의 로직을 통틀어 "계산기" 자체를 구동하는 인터페이스로 제공하는 게 더욱 직관적이기 때문입니다.

그런 면에서 퍼사드 패턴이 가장 깔끔하게 문제를 푸는 Best Practice라고 생각했습니다.
(다만 아직 디자인 패턴을 공부하면서 푸는 거라, 제대로 구현했는지는 모르겠군요. 😭)

따라서 어떤 서브 시스템 클래스들을 핸들링하기 위해 이 로직의 맨 앞쪽을 담당하는 객체를 MatrixCalculator라고 하겠습니다.

그리고 이 객체가 다루는 서브 시스템 클래스에는 다음과 같은 것들이 있습니다.

• Matrix: 데이터(행렬)를 책임지며, 연산에 맞춰 바뀐 결과를 적용합니다.
• RotateMatrixArrayPrinterStrategy: 출력을 담당합니다. 추후 클라이언트의 요구에 따라 계산 결과를 나타내는 방법이 달라질 수 있다고 문제에서 명시되었습니다. 따라서 같은 메서드로 다른 알고리즘을 적용하기 위해 전략 패턴을 적용했습니다.
• MatrixCommander: 이 행렬에 주어진 커맨드들을 같은 것끼리 압축시켜서 전달하는 로직만 책임지는 객체입니다. 이에 대한 최적화 방법 역시 다양해질 수 있으니 분리하는 게 맞다 판단했어요.

해당 코드 구현

class MatrixCalculator {
  constructor({ commands, matrix, printerStrategy }) {
    this.commander = commands;
    this.matrix = matrix;
    this.printerStrategy = printerStrategy;
  }

  run() {
    while (this.commander.commandLength) {
      const [command, count] = this.commander.command();

      if (command === this.commander.TYPE_SHIFT_ROW) {
        this.matrix.shiftRow(count);
      }

      if (command === this.commander.TYPE_ROTATE) {
        this.matrix.rotate(count);
      }
    }
  }

  getResult() {
    return this.printerStrategy.print();
  }
}

solution.js

결과적으로 반환할 코드에서는 계산기에 대한 인터페이스만 입력하면 끝! 더욱 직관적으로 로직을 해석할 수 있게 되었어요.

const solution = (rc, operations) => {
  const matrix = new Matrix(rc);

  const matrixCalculator = new MatrixCalculator({
    commands: new MatrixCommander({ commands: operations }),
    matrix,
    printerStrategy: new RotateMatrixArrayPrinterStrategy(matrix),
  });

  matrixCalculator.run();

  return matrixCalculator.getResult();
};

세부 구현 - 일련의 커맨드를 최적화하여 전달하는MatrixCommander

커맨더는 말 그대로 행렬의 커맨더만 압축하며, 내부 상태를 담을 자료구조는 큐로 구현되었습니다.

class Queue {
  constructor(queue) {
    this.queue = Array.isArray(queue) ? queue : [];
    this.rear = this.queue.length;
    this.front = 0;
  }

  enqueue(val) {
    this.queue.push(val);
    this.rear += 1;
  }

  dequeue() {
    const value = this.queue[this.front];
    delete this.queue[this.front];

    this.front += 1;
    return value;
  }

  get length() {
    return this.rear - this.front;
  }
}

class MatrixCommander {
  constructor({ commands }) {
    this.taskQueue = new Queue();
    this._init(commands);
  }

  get TYPE_SHIFT_ROW() {
    return 'ShiftRow';
  }

  get TYPE_ROTATE() {
    return 'Rotate';
  }

  _init(commands) {
    let prev = null;
    let count = 0;

    for (let i = 0; i < commands.length; i += 1) {
      const nowCommands = commands[i];

      if (prev === null || prev === nowCommands) {
        count += 1;
      } else {
        this.taskQueue.enqueue([prev, count]);

        count = 1;
      }

      prev = nowCommands;

      if (i === commands.length - 1) {
        this.taskQueue.enqueue([prev, count]);
      }
    }
  }
  
  command() {
    if (!this.taskQueue.length) return;

    // [command, runCount]
    return this.taskQueue.dequeue();
  }

  get commandLength() {
    return this.taskQueue.length;
  }
}

세부 구현 - 데이터를 저장하고 연산에 따라 조작하는 Matrix

Matrix 객체의 경우 각 커맨더에서 나온 현재의 커맨드에 따라 MatrixCalculator가 메서드를 호출시키는데요. 이에 맞춰 연산을 하고 데이터를 반영합니다.

내부 데이터의 경우 위에서 서술했던 3개의 그룹(left, right, main)
으로 분류하고 구현했어요!

class Node {
  constructor(value) {
    this.value = value;
    this.next = null;
    this.prev = null;
  }
}

class Deque {
  constructor() {
    this.init();
  }

  init() {
    this.count = 0;
    this.front = null;
    this.rear = null;
  }

  unshift(value) {
    const node = new Node(value);

    if (!this.front) {
      this.front = node;
      this.rear = node;
    } else {
      const cachedPrevFront = this.front;
      cachedPrevFront.prev = node;

      this.front = node;

      node.next = cachedPrevFront;
    }

    this.count += 1;
    return this.count;
  }

  shift() {
    if (this.count === 0) return null;

    const value = this.front.value;

    if (this.count === 1) {
      this.init();
    } else {
      this.front = this.front.next;
      this.front.prev = null;
      this.count -= 1;
    }

    return value;
  }

  push(value) {
    const node = new Node(value);

    if (this.count === 0) {
      this.front = node;
      this.rear = node;
    } else {
      const cachedPrevRear = this.rear;
      cachedPrevRear.next = node;

      node.prev = cachedPrevRear;

      this.rear = node;
    }

    this.count += 1;

    return this.count;
  }

  pop() {
    if (this.count === 0) return;

    const value = this.rear.value;

    if (this.count === 1) {
      this.init();
    } else {
      this.rear = this.rear.prev;
      this.rear.next = null;
      this.count -= 1;
    }

    return value;
  }

  getValue(idx) {
    if (idx >= this.count) return;
    let node = this.front;

    for (let i = 0; i < idx; i += 1) {
      node = node.next;
    }

    return node.value;
  }

  get rawArray() {
    let arr = [];
    let node = this.front;

    for (let i = 0; i < this.count; i += 1) {
      arr.push(node.value);
      node = node.next;
    }

    return arr;
  }

  get length() {
    return this.count;
  }
}
class Matrix {
  constructor(matrix) {
    this.left = new Deque();
    this.right = new Deque();
    this.main = new Deque();

    this._init(matrix);
  }

  _init(matrix) {
    for (let i = 0; i < matrix.length; i += 1) {
      const row = matrix[i];
      const deque = new Deque();

      row.forEach((val) => {
        deque.push(val);
      });

      this.left.push(deque.shift());
      this.right.push(deque.pop());
      this.main.push(deque);
    }
  }

  rotate(count) {
    let remainCount = count % (this.main.front.value.length * 2 + this.left.length + this.right.length);

    while (remainCount) {
      remainCount -= 1;

      this.main.front.value.unshift(this.left.shift());
      this.right.unshift(this.main.front.value.pop());
      this.main.rear.value.push(this.right.pop());
      this.left.push(this.main.rear.value.shift());
    }
  }

  shiftRow(count) {
    let remainCount = count % this.main.length;

    while (remainCount) {
      remainCount -= 1;

      this.main.unshift(this.main.pop());

      this.left.unshift(this.left.pop());
      this.right.unshift(this.right.pop());
    }
  }
}

세부 구현 - 연산에 따른 최종 결과를 반환하는 RotateMatrixArrayPrinterStrategy

이를 상속할 객체의 경우, 다른 하위 클래스들이 아직은 구현되지 않아 구현하지 않았어요. 이를 상속하는 로직을 만드는 건 어렵지 않으니까요!

matrix 객체의 데이터를 상태로 갖고 있으며, 원할 때 이 print 내부 알고리즘을 적용하여 결과 값을 배열 형태로 반환하도록 구현했어요.

class RotateMatrixArrayPrinterStrategy {
  constructor(matrix) {
    this.matrix = matrix;
  }

  print() {
    let result = [];

    const leftArr = this.matrix.left.rawArray;
    const mainArr = this.matrix.main.rawArray;
    const rightArr = this.matrix.right.rawArray;

    for (let i = 0; i < mainArr.length; i += 1) {
      const row = [];

      row.push(leftArr[i]);
      row.push(...mainArr[i].rawArray);
      row.push(rightArr[i]);

      result.push(row);
    }

    return result;
  }
}

결과 코드

전체 코드를 쓴 결과는 다음과 같구요!

class Node {
  constructor(value) {
    this.value = value;
    this.next = null;
    this.prev = null;
  }
}

class Deque {
  constructor() {
    this.init();
  }

  init() {
    this.count = 0;
    this.front = null;
    this.rear = null;
  }

  unshift(value) {
    const node = new Node(value);

    if (!this.front) {
      this.front = node;
      this.rear = node;
    } else {
      const cachedPrevFront = this.front;
      cachedPrevFront.prev = node;

      this.front = node;

      node.next = cachedPrevFront;
    }

    this.count += 1;
    return this.count;
  }

  shift() {
    if (this.count === 0) return null;

    const value = this.front.value;

    if (this.count === 1) {
      this.init();
    } else {
      this.front = this.front.next;
      this.front.prev = null;
      this.count -= 1;
    }

    return value;
  }

  push(value) {
    const node = new Node(value);

    if (this.count === 0) {
      this.front = node;
      this.rear = node;
    } else {
      const cachedPrevRear = this.rear;
      cachedPrevRear.next = node;

      node.prev = cachedPrevRear;

      this.rear = node;
    }

    this.count += 1;

    return this.count;
  }

  pop() {
    if (this.count === 0) return;

    const value = this.rear.value;

    if (this.count === 1) {
      this.init();
    } else {
      this.rear = this.rear.prev;
      this.rear.next = null;
      this.count -= 1;
    }

    return value;
  }

  getValue(idx) {
    if (idx >= this.count) return;
    let node = this.front;

    for (let i = 0; i < idx; i += 1) {
      node = node.next;
    }

    return node.value;
  }

  get rawArray() {
    let arr = [];
    let node = this.front;

    for (let i = 0; i < this.count; i += 1) {
      arr.push(node.value);
      node = node.next;
    }

    return arr;
  }

  get length() {
    return this.count;
  }
}

class Queue {
  constructor(queue) {
    this.queue = Array.isArray(queue) ? queue : [];
    this.rear = this.queue.length;
    this.front = 0;
  }

  enqueue(val) {
    this.queue.push(val);
    this.rear += 1;
  }

  dequeue() {
    const value = this.queue[this.front];
    delete this.queue[this.front];

    this.front += 1;
    return value;
  }

  get length() {
    return this.rear - this.front;
  }
}

class MatrixCommandar {
  constructor({ commands }) {
    this.taskQueue = new Queue();
    this._init(commands);
  }

  get TYPE_SHIFT_ROW() {
    return 'ShiftRow';
  }

  get TYPE_ROTATE() {
    return 'Rotate';
  }

  _init(commands) {
    let prev = null;
    let count = 0;

    for (let i = 0; i < commands.length; i += 1) {
      const nowCommands = commands[i];

      if (prev === null || prev === nowCommands) {
        count += 1;
      } else {
        this.taskQueue.enqueue([prev, count]);

        count = 1;
      }

      prev = nowCommands;

      if (i === commands.length - 1) {
        this.taskQueue.enqueue([prev, count]);
      }
    }
  }

  command() {
    if (!this.taskQueue.length) return;

    // [command, runCount]
    return this.taskQueue.dequeue();
  }

  get commandLength() {
    return this.taskQueue.length;
  }
}

class Matrix {
  constructor(matrix) {
    this.left = new Deque();
    this.right = new Deque();
    this.main = new Deque();

    this._init(matrix);
  }

  _init(matrix) {
    for (let i = 0; i < matrix.length; i += 1) {
      const row = matrix[i];
      const deque = new Deque();

      row.forEach((val) => {
        deque.push(val);
      });

      this.left.push(deque.shift());
      this.right.push(deque.pop());
      this.main.push(deque);
    }
  }

  rotate(count) {
    let remainCount = count % (this.main.front.value.length * 2 + this.left.length + this.right.length);

    while (remainCount) {
      remainCount -= 1;

      this.main.front.value.unshift(this.left.shift());
      this.right.unshift(this.main.front.value.pop());
      this.main.rear.value.push(this.right.pop());
      this.left.push(this.main.rear.value.shift());
    }
  }

  shiftRow(count) {
    let remainCount = count % this.main.length;

    while (remainCount) {
      remainCount -= 1;

      this.main.unshift(this.main.pop());

      this.left.unshift(this.left.pop());
      this.right.unshift(this.right.pop());
    }
  }
}

class RotateMatrixArrayPrinterStrategy {
  constructor(matrix) {
    this.matrix = matrix;
  }

  print() {
    let result = [];

    const leftArr = this.matrix.left.rawArray;
    const mainArr = this.matrix.main.rawArray;
    const rightArr = this.matrix.right.rawArray;

    for (let i = 0; i < mainArr.length; i += 1) {
      const row = [];

      row.push(leftArr[i]);
      row.push(...mainArr[i].rawArray);
      row.push(rightArr[i]);

      result.push(row);
    }

    return result;
  }
}

class MatrixCalculator {
  constructor({ commands, matrix, printerStrategy }) {
    this.commandar = commands;
    this.matrix = matrix;
    this.printerStrategy = printerStrategy;
  }

  run() {
    while (this.commandar.commandLength) {
      const [command, count] = this.commandar.command();

      if (command === this.commandar.TYPE_SHIFT_ROW) {
        this.matrix.shiftRow(count);
      }

      if (command === this.commandar.TYPE_ROTATE) {
        this.matrix.rotate(count);
      }
    }
  }

  getResult() {
    return this.printerStrategy.print();
  }
}

const solution = (rc, operations) => {
  const matrix = new Matrix(rc);

  const matrixCalculator = new MatrixCalculator({
    commands: new MatrixCommandar({ commands: operations }),
    matrix,
    printerStrategy: new RotateMatrixArrayPrinterStrategy(matrix),
  });

  matrixCalculator.run();

  return matrixCalculator.getResult();
};

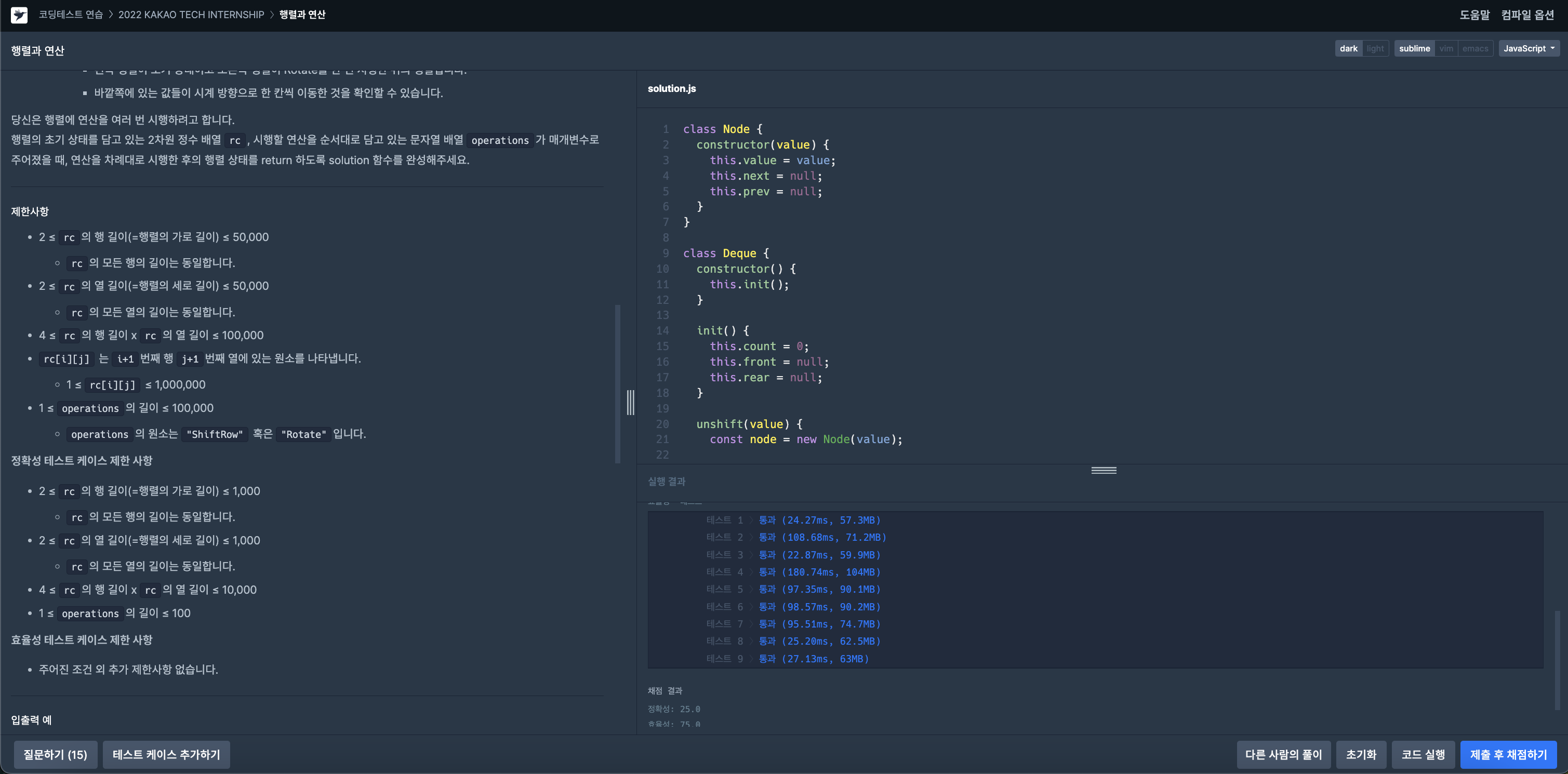
정말 빠른 속도로 문제를 해결할 수 있게 되었군요! 😉

👋🏻 마치며

이 문제는 우아해요. 왜냐하면 반드시 2차원 배열이라는 관점을 비틀면서도, 해답은 간단하게 자료구조를 사용하여 해결하기 때문입니다. 마치 기본에 집중하라고 알려주는 듯한 느낌이 들었어요!
심지어, 이게 인턴 문제이기 때문에 이러한 메시지가 정말 완벽하다고 생각합니다.
이 문제를 낸 분은 정말 지혜로운 프로그래머라는 생각이 들었어요! 👍

괜히 쉽게 풀 것을 어렵게 돌아간 감도 있기는 합니다. 하지만 연습 차원에서 무리해봤어요. 😉

저는 실무를 잘하고 싶고, 실무에서 오버엔지니어링을 피하기 위해서는 아이러니하게도 오버엔지니어링을 연습해야 하기 때문에 이렇게 풀어봤어요.

혹시나 제가 잘못 이해한 디자인 패턴이라던지, 더 좋은 방법이 있다면 공유해주시면 무한 감사드립니다! 🙆🏻

결국 나름대로 배운 것들을 적용해보고 복습하며 문제를 해결해서 기분이 좋아요!
다들 몸 챙기시면서, 즐거운 개발하시길 바랍니다 🙆🏻 이상!