백준/11404/Floyd/플로이드

백준/11404/Floyd/플로이드

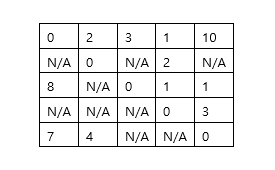
정점에서 정점까지에 모든 최단거리를 구해야하는 문제입니다.
i->j까지 어떤 버스를 거쳐서 최소 비용을 지불하고 갈 수 있는지에 대해 해결하면됩니다.
예제1을 예시로 풀어보겠습니다.
예제1)

예제1에서 입력받은 i(행)->j(열)로 가는 최소 버스 비용을 표기한 표입니다.
지금은 비어있는 곳도 많고 비용이 많은 곳도 있습니다.
이를 해결 하기 위해서는 i->(중간)->j 에서 중간 과정을 찾아 최소 비용을 표기해야합니다.
이를 위해 1,2,3,4,5 번째를 차례대로 대입하면 각 정류장을 거쳐서 가는 최소 비용이 표기됩니다.

for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			for (int z = 0; z < n; z++)
			{
				if (cost[j][i] + cost[i][z] < cost[j][z])
				{
					cost[j][z] = cost[j][i] + cost[i][z];
				}
			}

해당 과정을 계산하기 위해 3중 for문을 사용했습니다.

for (int i = 0; i < n; i++)
		fill(cost[i], cost[i] + n, INF);

fill 함수로 cost 배열에 무한값을 넣어준 이유는 처음에 중복되는 행선지로 부터
최소 값을 얻기 위해 채워넣었습니다.

풀이

1. 첫번째 풀이

#include<iostream>
#include<algorithm>
using namespace std;

int INF = 0x3f3f3f3f;
int cost[105][105];
int n;
int m;

void solve();
void solution();

void solve()
{
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			for (int z = 0; z < n; z++)
			{
				if (cost[j][i] + cost[i][z] < cost[j][z])
				{
					cost[j][z] = cost[j][i] + cost[i][z];
				}
			}

	solution();
}

void solution()
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			if (cost[i][j]==INF)
			{
				cout << '0' << ' ';
				continue;
			}
			cout << cost[i][j] << ' ';
		}
		cout << '\n';
	}
}

int main()
{
	cin.tie(0); cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> n >> m;
	for (int i = 0; i < n; i++)
		fill(cost[i], cost[i] + n, INF);

	for (int i = 0; i < m; i++)
	{
		int u, v, a;
		cin >> u >> v >> a;
		if(cost[u-1][v-1]>a)
			cost[u-1][v-1] = a;
	}

	for (int i = 0; i < n; i++)cost[i][i] = 0;

	solve();
}