경사하강법

미분(differentiation)

: 변수의 움직임에 따른 함수값의 변화를 측정하는 기법

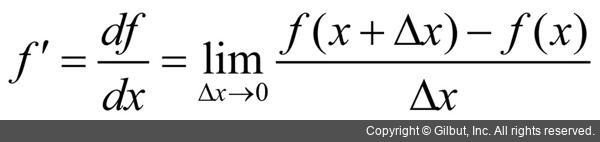
• 미분 = 변화율의 극한
• sympy.diff로 계산 가능
• 변화율을 0으로 보내면 점 (x,f(x))에서 접선의 기울기로 수렴함

왜 미분을 하는가?

• 점 (x, f(x))에서 접선의 기울기를 알면 어느 방향으로 움직여야 함수값이 증가/감소하는지 알 수 있음.
  • 미분값 더하기 --> 증가
  • 미분값 빼기 --> 감소
• 경사상승법 : 미분값을 더하여 함수의 극대값의 위치를 구하는 것
  경사하강법 : 미분값을 빼 함수의 극소값의 위치를 구하는 것
• --> 경사상승법/하강법은 극값에 도달하면 목적함수의 최적화가 끝남

경사하강법 알고리즘

var = init
grad = gradient(var)
while(abs(grad) > eps):		# eps: 종료조건
    var = var - lr * grad	# lr: 학습률
    grad = gradient(var)	# var를 계속 업데이트하고 미분값 빼기 반복

편미분

• 위에는 변수 하나에 대한 단순한 개념 설명이었음.
• 변수가 벡터인 경우, n차원 공간이기 때문에 많은 방향이 존재함. --> 편미분
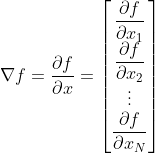
• 편미분은 변수별로 편미분을 계산. (d차원 -> d번 편미분)
• 변수들의 편미분값을 벡터로 표현한 것 = 그레디언트 벡터
  

내용 추가 약속~