✍ 문제
한 배열 A[1], A[2], …, A[n]에 대해서, 부 배열은 A[i], A[i+1], …, A[j-1], A[j] (단, 1 ≤ i ≤ j ≤ n)을 말한다. 이러한 부 배열의 합은 A[i]+…+A[j]를 의미한다. 각 원소가 정수인 두 배열 A[1], …, A[n]과 B[1], …, B[m]이 주어졌을 때, A의 부 배열의 합에 B의 부 배열의 합을 더해서 T가 되는 모든 부 배열 쌍의 개수를 구하는 프로그램을 작성하시오.
예를 들어, A = {1, 3, 1, 2}, B = {1, 3, 2}, T=5인 경우, 부 배열 쌍의 개수는 다음의 7가지 경우가 있다.
T(=5) = A[1] + B[1] + B[2]
= A[1] + A[2] + B[1]
= A[2] + B[3]
= A[2] + A[3] + B[1]
= A[3] + B[1] + B[2]
= A[3] + A[4] + B[3]
= A[4] + B[2]
✍ 입력
첫째 줄에 T(-1,000,000,000 ≤ T ≤ 1,000,000,000)가 주어진다. 다음 줄에는 n(1 ≤ n ≤ 1,000)이 주어지고, 그 다음 줄에 n개의 정수로 A[1], …, A[n]이 주어진다. 다음 줄에는 m(1 ≤ m ≤ 1,000)이 주어지고, 그 다음 줄에 m개의 정수로 B[1], …, B[m]이 주어진다. 각각의 배열 원소는 절댓값이 1,000,000을 넘지 않는 정수이다.
✍ 출력
첫째 줄에 답을 출력한다. 가능한 경우가 한 가지도 없을 경우에는 0을 출력한다.
✅ 코드
#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;
int t, n, m;
int a[1001], b[1001];
long long sa[500501], sb[500501]; //부분합 배열
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int temp;
cin >> t;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> temp;
a[i] = temp;
}
//배열 a의 부분합 배열 sa 계산
int aidx = 0; int sum_a = 0;
for (int i = 0; i < n; i++) {
sa[aidx++] = a[i];
sum_a = a[i];
for (int j = i+1; j < n; j++) {
sum_a += a[j];
sa[aidx++] = sum_a;
}
}
cin >> m;
for (int i = 0; i < m; i++) {
cin >> temp;
b[i] = temp;
}
//배열 b의 부분합 배열 sb 계산
int bidx = 0; int sum_b = 0;
for (int i = 0; i < m; i++) {
sb[bidx++] = b[i];
sum_b = b[i];
for (int j = i+1; j < m; j++) {
sum_b += b[j];
sb[bidx++] = sum_b;
}
}
//부분합 배열 오름차순 정리
sort(sa, sa+aidx);
sort(sb, sb+bidx);
int al = 0; int br = bidx -1;
long long sum = 0;
long long result = 0;
while (al < aidx && br >= 0) {
sum = sa[al] + sb[br];
if (sum < t) al++;
else if (sum > t) br--;
else if (sum == t) {
long long same_a = 1;
long long same_b = 1;
for (int i = al + 1; i < aidx; i++) {
if (sa[i] == sa[al]) same_a++;
else break;
}
for (int i = br - 1; i >= 0; i--) {
if (sb[i] == sb[br]) same_b++;
else break;
}
result += same_a * same_b;
al += same_a;
br -= same_b;
}
}
cout << result;
return 0;
}✅ 코드풀이
이 문제에서의 핵심은 시간복잡도⏰ 를 고려하는 것이다.
가장 무식한(?) 방법으로는 배열의 원소를 1개, 2개 ... t개 사용하는 경우의 수를 각각 구해서 더해서 구할 수 있다. 그런데 T의 범위의 최대값이 10억이다. 각 경우의 수가 10개씩만 나와도 100억번 이상의 연산을 해야된다는 건데 C++ 기준 1초에 1억번의 연산을 진행한다고 가정하면 제한 시간인 2초 안에 실행하는 것은 불가능하다.
🤔 어떻게 하면 시간 복잡도를 줄일 수 있을까?
우리가 구하고자 하는 것이 "부분합의 합" 임을 떠올려보자. 배열 A, B에서 나올 수 있는 부분합들의 합을 T로 만드는 경우의 수를 구하는 것이므로 각 배열의 부분합의 값을 저장하는 배열(sa, sb)을 선언하고 그 값을 채워볼 수 있다.
🚨 이 때 주의할 점!
입력으로 받는 배열 원소의 범위는 -10억 이상 10억 이하이다. 그렇다면 그 원소들의 합으로 계산되는 부분합 배열의 원소는 int 범위를 초과할 수 있다. 따라서 부분합 배열의 원소 자료형은 반드시 long long으로 선언해야 한다.
(int형은 대략 절댓값 21억 이하의 값들까지 표현가능 함을 외워두자)
이 문제를 풀기위한 중요 아이디어 중 하나인 부분합 배열의 선언까지 생각해냈다면 거의 다 온 것이다! 이제는 이 부분합 배열을 이용하여 결론적으로 그 합을 T로 만드는 경우의 수를 구하면 된다.
🤔 하나는 작은 쪽부터, 하나는 큰 쪽부터!
a의 부분합 배열(sa)의 원소 하나와 b의 부분합 배열(sb)의 원소 하나를 더해 T를 만들면 되는 상황이다. 이 때 떠올릴 수 있는 아이디어는 sa 배열은 원소가 작은 것부터, sb 배열은 원소가 큰 것부터 탐색하는 것이다.
이 경우에 만약 두 배열에서 고른 원소의 합이 T보다 크다면 값을 줄여야 하므로 내림차순으로 탐색하는 sb 배열의 index를 줄이면 되고, 반대로 작다면 오름차순으로 탐색하는 sa 배열의 index를 키우면 된다!
이것을 구현하기 위해 두 부분합 배열을 sort를 이용해 오름차순 정리를 해주고, 탐색할 index의 값을 al = 0 (가장 작은 원소 위치), br = bidx - 1 (가장 큰 원소 위치)로 초기화시켜준다.
while (al < aidx && br >= 0) {
sum = sa[al] + sb[br];
if (sum < t) al++;
else if (sum > t) br--;
else if (sum == t) {
long long same_a = 1;
long long same_b = 1;
for (int i = al + 1; i < aidx; i++) {
if (sa[i] == sa[al]) same_a++;
else break;
}
for (int i = br - 1; i >= 0; i--) {
if (sb[i] == sb[br]) same_b++;
else break;
}
result += same_a * same_b;
al += same_a;
br -= same_b;
}
}그리고 while문을 돌며 경우의 수를 세주면 되는데 이 내부에서 시간을 줄일 수 있는 한 가지 방법이 더 있다. sum = t인 경우, 즉 원소의 합이 우리가 원하는 값으로 계산된 경우, 만약 앞으로 탐색을 진행할 방향에 동일한 원소가 있다면 그 개수를 세어 한 번에 경우의 수를 계산하는 것이다.
글로 설명하자니 이해가 어려울 것 같아 그림으로 표현해보았다!
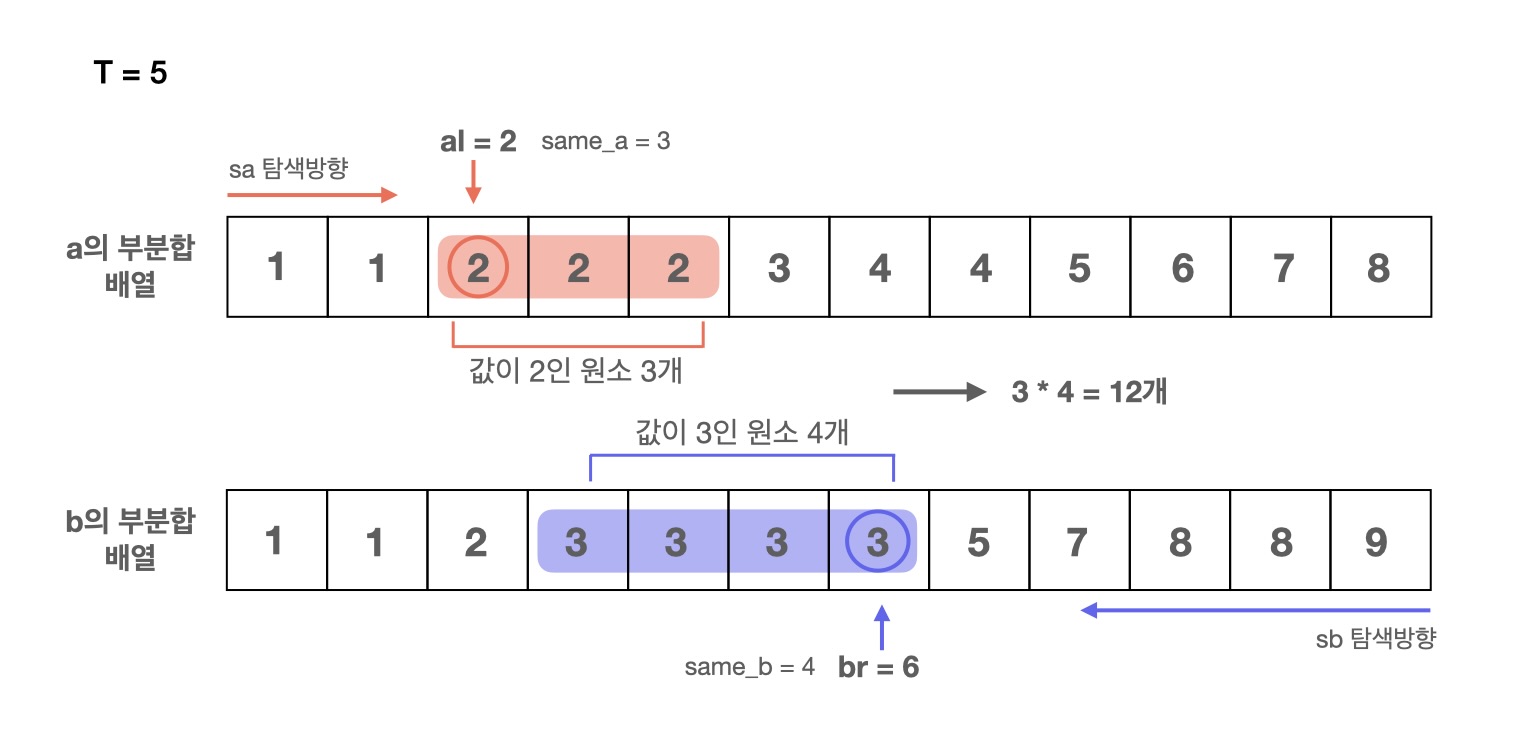
위 그림에 해당하는 부분이 else if (sum == t) 블록 안의 코드이다.
🔐 최종 정리를 해보자!
- 배열 a, b의 부분합 배열 sa, sb 계산
- sa는 오름차순, sb는 내림차순으로 탐색하며 경우의 수 계산
- 합이 T가 되는 경우의 수를 찾은 경우, 그 원소와 값이 동일한 원소가 있는지 확인
❗ 떠올려야 하는 아이디어가 두 개나 있어서 풀기 어려웠던 문제였다. 다양한 문제를 풀며 적절한 아이디어를 떠올릴 수 있는 연습을 해야되겠다는 생각이 든다! 그럴려면 기본적으로 알고리즘이나 유용한 자료구조에 대해 잘 이해하고 많이 연습해봐야 할 것 같다 😵💫
