[알고리즘] 힙(Heap) 자료구조

JINJIN·2023년 11월 10일
JavaScriptalgorismuseful
0

알고리즘

목록 보기
2/3

자주 사용하게 되는 알고리즘에 대해서 하나씩 알아보겠습니다.

힙(Heap)

힙의 정의와 특성

힙(Heap)은 컴퓨터 과학에서 사용되는 특별한 트리 기반의 자료구조입니다. 기본적으로 힙은 다음과 같은 두 가지 특징을 가진 완전 이진 트리(Complete Binary Tree)입니다.

  • 완전 이진 트리

    힙은 완전 이진 트리의 형태를 취하고 있습니다. 완전 이진 트리란, 모든 레벨이 노드들로 가득 차 있으며, 마지막 레벨의 노드들은 왼쪽부터 차례대로 채워져 있는 트리를 말합니다. 이러한 구조 덕분에 힙은 배열을 사용하여 효율적으로 표현할 수 있으며, 각 노드의 부모 또는 자식 노드에 접근하기 위한 계산이 간단합니다.

  • 힙 속성(Heap Property)

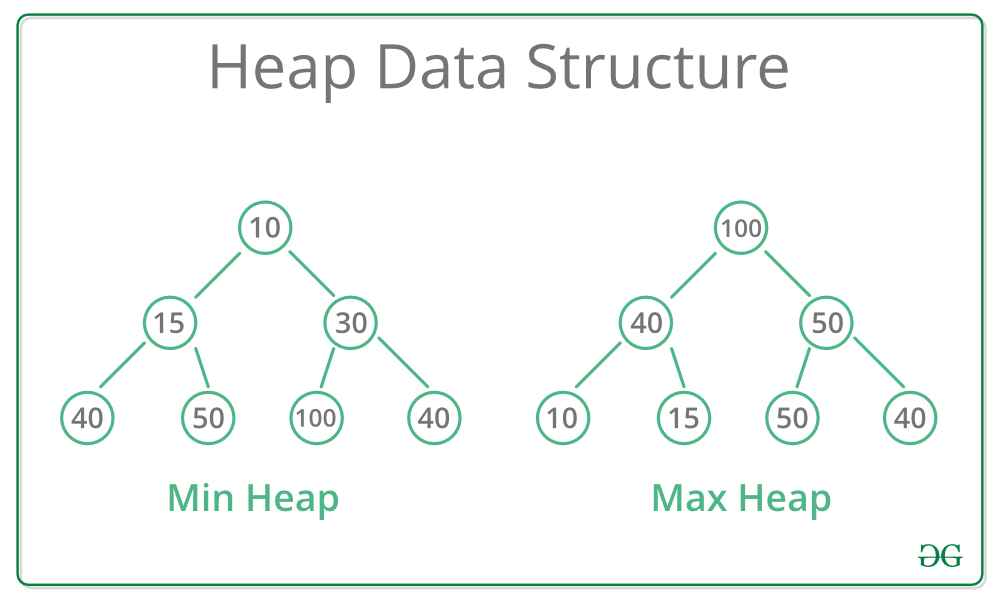
    힙에는 두 종류가 있습니다. 최대 힙(Max Heap)에서는 각 노드의 값이 그 자식 노드들의 값보다 크거나 같습니다. 즉, 힙의 루트에는 힙에 있는 가장 큰 값이 위치합니다. 반대로 최소 힙(Min Heap)에서는 각 노드의 값이 그 자식 노드들의 값보다 작거나 같습니다. 여기서는 힙의 루트에 가장 작은 값이 위치합니다.


최소 힙과 최대 힙

최소 힙(Min Heap)

최소 힙에서는 부모 노드의 값이 자식 노드의 값보다 항상 작거나 같습니다. 이 속성으로 인해 트리의 루트, 즉 가장 상위에 있는 노드는 전체 트리에서 가장 작은 요소를 가지게 됩니다. 이것은 최소 힙의 가장 중요한 특성입니다.

최소 힙의 주요 연산

삽입(Insert)

  • 새로운 요소를 힙에 삽입할 때, 요소는 먼저 트리의 가장 낮은 레벨, 가장 오른쪽에 있는 빈 자리에 추가됩니다. 그런 다음, 힙의 속성을 유지하기 위해 필요한 경우 부모 노드와 위치를 교환하는 "상향 조정(up-heap)" 과정을 거칩니다.

삭제(Remove)

  • 힙에서 요소를 삭제할 때, 일반적으로 루트 노드(최소값)가 제거됩니다. 루트 노드를 삭제한 후, 힙의 마지막 요소를 루트로 이동시키고, 힙 속성을 유지하기 위해 "하향 조정(down-heap)" 과정을 거칩니다.

최대 힙(Max Heap)

최대 힙은 최소 힙의 반대 개념으로, 부모 노드의 값이 자식 노드의 값보다 항상 크거나 같습니다. 이는 최대 힙의 루트가 전체 트리에서 가장 큰 요소를 가지고 있다는 것을 의미합니다.

최대 힙의 주요 연산

삽입(Insert)

  • 새로운 요소가 힙에 추가될 때, 이 요소는 먼저 트리의 마지막 위치에 삽입된 다음, 부모 노드와 비교하며 필요한 경우 위치를 교환하여 최대 힙 속성을 만족시키는 위치로 올라갑니다.

삭제(Remove)

  • 힙에서 요소를 삭제할 때, 보통 루트 노드(최대값)가 제거됩니다. 루트 노드를 제거한 후에는 힙의 마지막 요소를 루트로 이동시키고, 다시 최대 힙 속성을 만족시키기 위해 위치를 조정합니다.

힙의 구현

자바스크립트에는 Java나 C++과 같은 다른 언어에서 제공되는 표준 라이브러리에 포함된 힙(Heap) 자료구조가 기본적으로 내장되어 있지 않습니다.

자바스크립트에서 힙을 구현하는 가장 일반적인 방법은 배열을 사용하고, 힙의 속성을 유지하기 위해 삽입, 삭제, 힙 재구성 등의 메커니즘을 수동으로 코딩하는 것입니다. 이는 힙이 필요한 알고리즘을 작성할 때, 추가적인 작업이 필요함을 의미합니다.

사실 외부 라이브러리를 사용해도 됩니다.


배열을 이용한 힙의 구현 방법

자바스크립트에서 힙, 특히 최소 힙(Min Heap)을 구현하는 것은 일반적으로 배열을 사용하여 힙의 각 요소를 저장하고 관리합니다. 아래에는 최소 힙을 구현하는 기본적인 방법을 하나씩 설명하겠습니다.

1. 힙 클래스 구조

이 클래스는 heap이라는 배열을 포함하여, 힙 내의 모든 요소를 저장합니다.

class MinHeap {
  constructor() {
    this.heap = []; // 힙의 구조를 배열로 초기화합니다.
  }
}

2. 부모 및 자식 노드의 인덱스 계산

힙에서 부모 및 자식 노드의 인덱스를 계산하는 것은 중요합니다. 완전 이진 트리의 성질을 이용하여 배열 내의 인덱스를 통해 이를 쉽게 계산할 수 있습니다.

class MinHeap {
  // ...

  // i번째 요소의 부모 노드의 인덱스를 반환합니다.
  getParentIndex(i) {
    return Math.floor((i - 1) / 2);
  }

  // i번째 요소의 왼쪽 자식 노드의 인덱스를 반환합니다.
  getLeftChildIndex(i) {
    return 2 * i + 1;
  }

  // i번째 요소의 오른쪽 자식 노드의 인덱스를 반환합니다.
  getRightChildIndex(i) {
    return 2 * i + 2;
  }
}

3. 요소 교환

힙 내부에서 요소의 위치를 교환하는 메소드입니다.

class MinHeap {
  // ...

  // 배열 내의 두 요소를 서로 바꾸는 함수입니다.
  swap(i1, i2) {
    [this.heap[i1], this.heap[i2]] = [this.heap[i2], this.heap[i1]]
  }
}

4. 삽입 메소드

새로운 요소를 힙에 삽입하는 메소드입니다. 요소를 배열의 마지막에 추가한 후, 힙 속성을 유지하기 위해 부모 노드와의 위치를 조정합니다.

class MinHeap {
  // ...

  // 힙에 새로운 값을 삽입합니다. 삽입 후, 힙의 조건을 만족시키기 위해 재정렬합니다.
  insert(value) {
    this.heap.push(value); // 값을 힙에 삽입합니다.
    let index = this.heap.length - 1; // 삽입된 값의 인덱스입니다.
    let parent = this.getParentIndex(index); // 삽입된 값의 부모 노드의 인덱스입니다.

    // 새로 삽입된 값이 부모 노드보다 작은 동안 (최소 힙 조건을 만족하지 않는 동안),
    // 부모 노드와 자리를 바꿉니다.
    while (index > 0 && this.heap[parent] > this.heap[index]) {
      this.swap(parent, index);
      index = parent;
      parent = this.getParentIndex(index);
    }
  }
}

5. 삭제 메소드

힙에서 요소를 제거하는 메소드입니다. 일반적으로 힙에서는 루트(가장 작은 요소)를 제거합니다.

class MinHeap {
  // ...

  // 힙에서 최소값을 제거하고 반환합니다.
  remove() {
    const smallest = this.heap[0]; // 힙의 최소값(루트)을 임시 저장합니다.
    const last = this.heap.pop(); // 힙의 마지막 요소를 제거합니다.
    if (this.heap.length > 0) {
      this.heap[0] = last; // 힙의 루트에 마지막 요소를 할당합니다.
      this.heapify(0); // 힙의 조건을 만족시키기 위해 재정렬합니다.
    }
    return smallest; // 힙에서 제거한 최소값을 반환합니다.
  }
}

6. 힙 재구성

제거 연산 후에 힙 속성을 재구성하는 메소드입니다. 이는 힙의 루트에서 시작하여 재귀적으로 힙을 재구성합니다.

class MinHeap {
  // ...

  // 주어진 인덱스에서 시작하여 힙의 조건을 만족시키도록 재정렬합니다.
  heapify(index) {
    let left = this.getLeftChildIndex(index); // 왼쪽 자식 노드의 인덱스입니다.
    let right = this.getRightChildIndex(index); // 오른쪽 자식 노드의 인덱스입니다.
    let smallest = index; // 가장 작은 값을 가진 노드의 인덱스를 저장합니다.

    // 왼쪽 자식 노드가 존재하고, 현재 노드보다 작으면 smallest를 갱신합니다.
    if (left < this.heap.length && this.heap[left] < this.heap[smallest]) {
      smallest = left;
    }
    // 오른쪽 자식 노드가 존재하고, 현재 가장 작은 값보다 작으면 smallest를 갱신합니다.
    if (right < this.heap.length && this.heap[right] < this.heap[smallest]) {
      smallest = right;
    }
    // 가장 작은 값이 현재 노드가 아니라면, 위치를 바꾸고 재귀적으로 heapify를 호출합니다.
    if (smallest !== index) {
      this.swap(index, smallest);
      this.heapify(smallest);
    }
  }
}

7. 힙의 최소값 확인

힙의 최소값(루트 노드)을 확인하는 메소드입니다.

class MinHeap {
  // ...

  // 힙의 최소값(루트)을 반환합니다.
  peek() {
    return this.heap[0];
  }
}

8. 힙의 크기 확인

힙의 크기(요소의 수)를 반환하는 메소드입니다.

class MinHeap {
  // ...

  // 힙의 크기(요소의 개수)를 반환합니다.
  size() {
    return this.heap.length;
  }
}

인덱스 관계(부모-자식) 설명

힙은 완전 이진 트리의 형태를 가지며, 자바스크립트에서는 배열을 사용하여 효율적으로 구현됩니다. 이때, 부모-자식 간의 인덱스 관계를 이해하는 것이 중요합니다. 이 관계는 힙에서 노드를 삽입, 삭제, 재정렬할 때 필요한 기본 연산입니다.

예시

배열을 사용한 힙에서 이러한 인덱스 계산이 어떻게 적용되는지 예를 들어 설명하겠습니다.

[15, 10, 12, 5, 8, 7]

예를 들어, 배열이 다음과 같이 주어진 경우

  1. 인덱스 0의 요소(값: 15)는 루트 노드입니다.
  2. 인덱스 1의 요소(값: 10)는 인덱스 0의 왼쪽 자식입니다.
  3. 인덱스 2의 요소(값: 12)는 인덱스 0의 오른쪽 자식입니다.
  4. 인덱스 1의 요소(값: 10)의 왼쪽 자식은 인덱스 3에 있습니다(값: 5).
  5. 인덱스 1의 요소(값: 10)의 오른쪽 자식은 인덱스 4에 있습니다(값: 8).
  6. 그리고 이런 식으로 계속됩니다.

이 인덱스 관계는 힙에 새로운 요소를 추가하거나, 요소를 삭제할 때 힙의 속성을 유지하기 위해 필요한 "상향 조정(up-heap)" 또는 "하향 조정(down-heap)" 과정에 중요합니다.


힙의 사용 사례

힙, 특히 최소 힙과 최대 힙은 데이터를 관리하는 데 있어서 다양한 상황에서 유용하게 사용됩니다. 그 중 가장 많이 사용하는 사례는 우선 순위 큐(Priority Queue)와 힙을 사용한 정렬 방식(Heap sort)을 가장 많이 사용합니다.


1. 우선 순위 큐(Priority Queue)

우선순위 큐는 일반 큐와 비슷하지만, 각 요소가 우선순위를 가지고 있으며, 우선순위가 높은 요소가 먼저 제거됩니다.

우선 순위 큐의 특징

  • 우선순위 기반 처리
    요소들이 FIFO(First In, First Out) 순서대로 나오는 것이 아니라, 각 요소의 우선순위에 따라 처리됩니다.

  • 다양한 구현 방식
    배열, 연결 리스트, 힙 등 다양한 방법으로 구현할 수 있습니다. 그 중 힙을 사용한 구현이 가장 효율적입니다.

  • 응용 분야
    우선순위 큐는 시뮬레이션 시스템, 데이터 압축, 라우팅 알고리즘, 네트워크 대역폭 관리 등 다양한 분야에서 활용됩니다.


힙을 사용한 우선순위 큐의 장점

  • 빠른 삽입과 삭제
    힙을 사용하면 요소의 삽입과 삭제(특히, 최소값 또는 최대값의 삭제)가 O(log n) 시간에 처리될 수 있습니다.

  • 동적 크기 조정
    배열을 기반으로 하는 힙은 크기가 동적으로 조정되므로, 요소의 삽입과 삭제가 자유롭습니다.


2. 힙 정렬(Heap Sort)

힙 정렬은 정렬 알고리즘 중 하나로, 힙 자료구조의 특성을 이용하여 배열을 정렬합니다.

힙 정렬의 특징

  • 효율적인 정렬 방법
    힙 정렬은 O(n log n)의 시간 복잡도를 가지며, 최악의 경우에도 이 시간 복잡도를 유지합니다.

  • 정렬 과정

    • 힙 구축: 주어진 배열로부터 최대 힙(Max Heap) 또는 최소 힙(Min Heap)을 구축합니다. 최대 힙은 내림차순 정렬, 최소 힙은 오름차순 정렬에 사용됩니다.

    • 요소 제거 및 재배치: 힙의 루트(최대값 또는 최소값)를 배열의 끝으로 이동시키고, 힙의 크기를 줄입니다. 이후 힙 속성을 유지하기 위해 재조정합니다.

    • 반복 과정: 위의 과정을 배열이 정렬될 때까지 반복합니다.


힙 정렬은 in-place 정렬이며, 추가적인 메모리를 거의 사용하지 않습니다. 그러나 힙 정렬은 퀵 정렬과 같은 다른 효율적인 정렬 알고리즘에 비해 일반적으로 느린 편입니다. 그럼에도 불구하고 최악의 경우에도 일정한 성능을 보장한다는 점에서 안정적인 정렬 방법으로 여겨집니다.


결론

힙은 자바스크립트에서 내장된 자료구조가 아니지만, 그 효율성과 유용성으로 인해 많은 알고리즘과 데이터 처리 상황에서 중요한 역할을 합니다.

자바스크립트에서 힙을 구현할 때는 배열을 사용해 부모-자식 노드 간의 관계를 관리하며, 삽입, 삭제, 재조정(heapify) 과정을 통해 힙의 속성을 유지합니다. 이러한 특징들로 인해 힙은 데이터를 동적으로 관리하고, 효율적으로 처리하는 데 매우 유용한 자료구조입니다.

profile
JINJIN
안녕하세요! 배우는 것을 좋아하는 개발자 JINJIN입니다.
이전 포스트

[알고리즘] BFS 그리고 DFS

다음 포스트

[알고리즘] 스택(Stack) / 큐(Queue)

0개의 댓글