[ MR 04. SWEA - 4534. 트리 흑백 색칠 ]
습관 만들기 1일 1코테 챌린지!
언어 : C++
문제
정점이 N개인 트리가 주어진다. 의석이는 각 정점을 검은색 아니면 하얀색 중 하나로 칠하려고 한다.
단, 어떤 간선으로 연결된 두 정점이 모두 검은색이면 안 된다. 색칠하는 것으로 가능한 경우의 수는 몇 가지인가?
예를 들면 위와 같은 트리가 있다고 하면
가능한 모든 색칠의 경우의 수는 (하얀색/하얀색), (하얀색/검은색), (검은색/하얀색), (검은색/검은색) [(1번정점의색/2번정점의색)]이지만,
위 조건을 만족하는 경우의 수는 (검은색/검은색)을 제외한 나머지 3개이다.
입력
첫 번째 줄에 테스트 케이스의 수 T가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 하나의 정수 N(2≤N≤100,000)이 주어진다.
다음 N-1개의 줄의 각 줄에는 두 정수 x,y가 공백으로 구분되어 주어진다.
이는 정점의 번호를 1번에서 N번까지로 매길 때 x번 정점과 y번 정점을
연결하는 간선이 있다는 의미이다.
주어진 그래프는 트리임이 보장된다.
출력
각 줄마다 "#T" (T는 테스트 케이스 번호)를 출력한 뒤, 트리의
각 정점을 색칠할 수 있는 경우의 수를 출력한다.
이 수는 매우 클 수 있으므로 1,000,000,007로 나눈 나머지를 출력하도록 한다.
내 풀이
접근방식
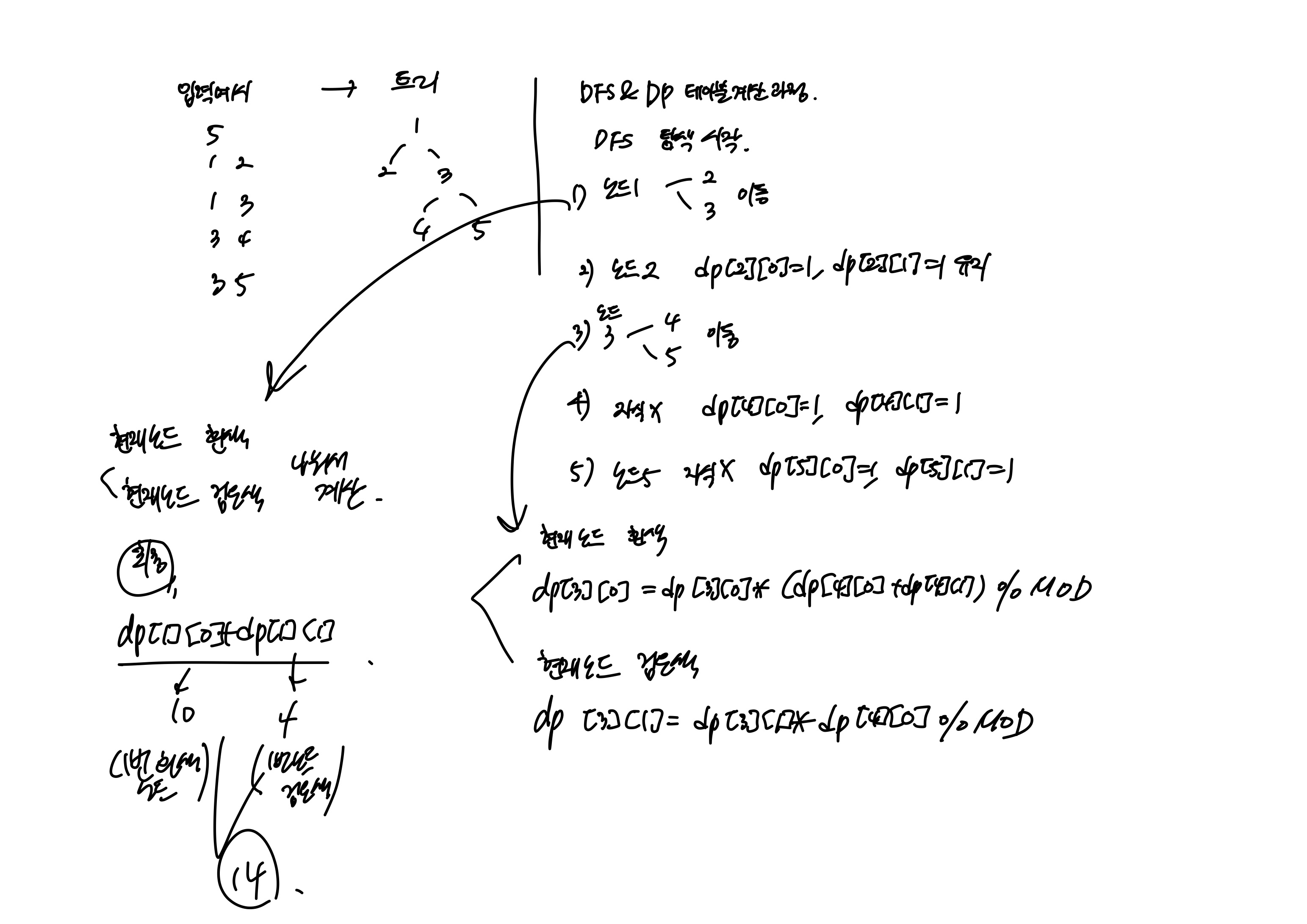
트리 구조 파악: 트리는 사이클이 없는 연결된 그래프.그래프 탐색 알고리즘을 사용하여 트리를 탐색할 수 있음.
DP 테이블 정의: 각 노드에 대해 두 가지 상태를 저장할 DP 테이블을 정의.
dp[u][0]은 노드 u가 흰색일 때 서브트리의 가능한 색칠 경우의 수,
dp[u][1]은 노드 u가 검은색일 때 서브트리의 가능한 색칠 경우의 수.DFS로 트리 탐색 및 DP 계산: 루트에서부터 DFS(깊이 우선 탐색)를 사용하여 각 노드의 DP 값을 계산.
결과 계산: 루트 노드에서 두 경우의 수를 합산하여 결과를 도출.
구체적인 구현 방법
트리의 각 노드를 DFS를 사용하여 탐색하고,
자식 노드들이 색칠될 수 있는 경우의 수를 누적하여 부모 노드의 경우의 수를 계산.
이를 위해 adj라는 인접 리스트를 사용하여 트리를 표현하고,
dp 테이블을 사용하여 각 노드의 상태를 저장.
// DFS를 이용하여 DP 값 계산
void dfs(int node, int parent) {
dp[node][0] = dp[node][1] = 1; // 초기화: 현재 노드가 흰색 또는 검은색일 때 경우의 수는 최소 1
for (int neighbor : adj[node]) {
if (neighbor == parent) continue; // 부모 노드는 건너뜀
dfs(neighbor, node); // 자식 노드에 대해 재귀적으로 DFS 호출
// 현재 노드가 흰색인 경우, 자식 노드는 흰색 또는 검은색이 될 수 있음
dp[node][0] = dp[node][0] * (dp[neighbor][0] + dp[neighbor][1]) % MOD;
// 현재 노드가 검은색인 경우, 자식 노드는 반드시 흰색이어야 함
dp[node][1] = dp[node][1] *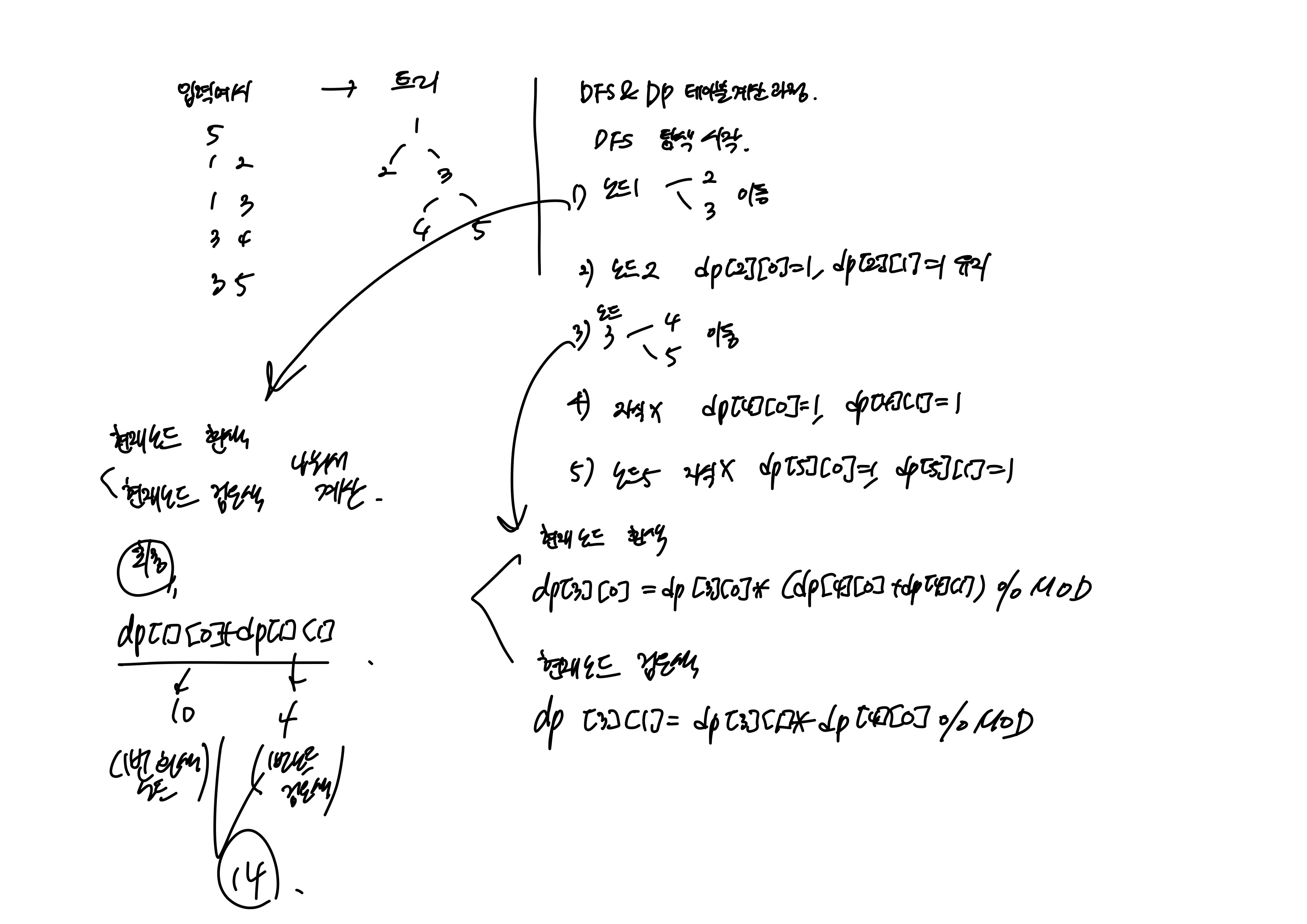
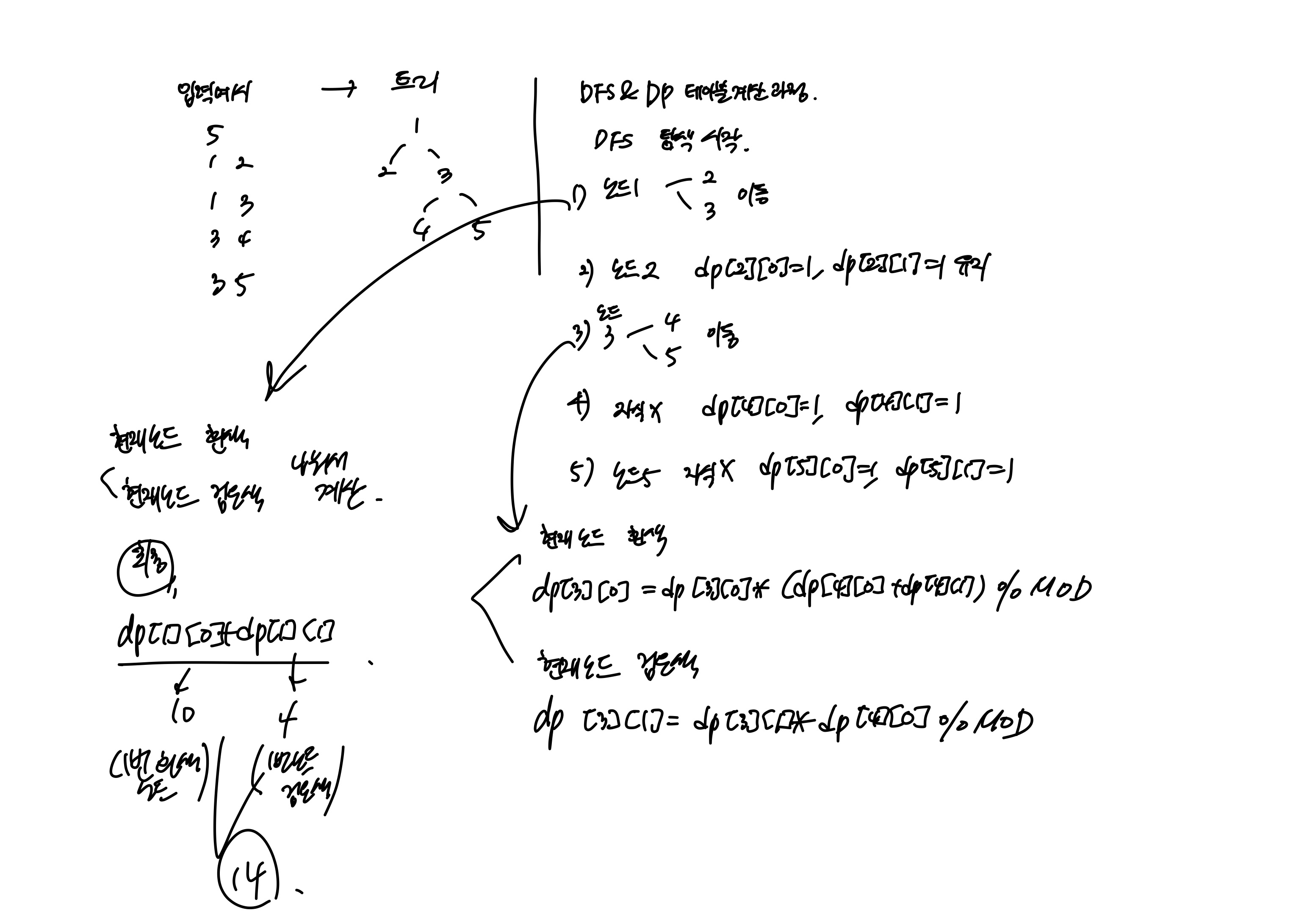
dp[neighbor][0] % MOD;
}
}
개념 정확하게 알고가기
DFS (Depth-First Search, 깊이 우선 탐색)
정의
DFS는 그래프 탐색 알고리즘 중 하나로, 시작 노드에서 출발하여 가능한 한 깊이 들어가서 탐색을 진행하고, 더 이상 갈 수 없으면 되돌아가면서 탐색을 계속하는 방식.주요 특징
스택을 이용한 탐색: 재귀 호출을 사용하면 자동으로 스택 구조를 이용.
모든 경로 탐색: 한 노드에서 출발하여 가능한 모든 경로를 탐색.
백트래킹: 더 이상 갈 곳이 없으면 한 단계 되돌아가서 다른 경로를 탐색.사용 시기
경로 탐색: 특정 시작점에서 모든 경로를 탐색할 때 유용.
사이클 탐지: 그래프에 사이클이 있는지 확인할 때 유용.
트리 탐색: 트리 구조에서 특정 노드를 찾거나, 서브트리의 성질을 조사할 때 사용.
DP (Dynamic Programming, 동적 계획법)
정의
DP는 복잡한 문제를 더 간단한 하위 문제로 나누어 해결하는 방법.
하위 문제의 결과를 저장해두고, 이를 조합하여 최종 문제를 해결.주요 특징
중복 계산 회피: 동일한 하위 문제를 여러 번 계산하지 않고,
한 번 계산한 결과를 저장하여 재사용.
메모이제이션: 계산한 결과를 저장하는 테이블(배열)을 이용.
최적 부분 구조: 큰 문제의 최적해는 작은 문제들의 최적해로부터 구할 수 있음.사용 시기
최적화 문제: 최대, 최소값을 구하는 문제에서 사용.
결과를 나눠서 계산: 문제를 부분 문제로 나누어 각 부분 문제의 결과를 저장하고
이를 조합하여 최종 결과를 구할 때 사용.
후기
너무 어려워...아직은 더 공부해야돼...