9465 > 스티커
😗 문제 설명
상근이의 여동생 상냥이는 문방구에서 스티커 2n개를 구매했다.
스티커는 그림 (a)와 같이 2행 n열로 배치되어 있다.
상냥이는 스티커를 이용해 책상을 꾸미려고 한다.
상냥이가 구매한 스티커의 품질은 매우 좋지 않다.
스티커 한 장을 떼면, 그 스티커와 변을 공유하는 스티커는 모두 찢어져서 사용할 수 없게 된다.
즉, 뗀 스티커의 왼쪽, 오른쪽, 위, 아래에 있는 스티커는 사용할 수 없게 된다.
모든 스티커를 붙일 수 없게된 상냥이는 각 스티커에 점수를 매기고, 점수의 합이 최대가 되게 스티커를 떼어내려고 한다.
먼저, 그림 (b)와 같이 각 스티커에 점수를 매겼다.
상냥이가 뗄 수 있는 스티커의 점수의 최댓값을 구하는 프로그램을 작성하시오.
즉, 2n개의 스티커 중에서 점수의 합이 최대가 되면서 서로 변을 공유 하지 않는 스티커 집합을 구해야 한다.
위의 그림의 경우에 점수가 50, 50, 100, 60인 스티커를 고르면, 점수는 260이 되고 이 것이 최대 점수이다. 가
장 높은 점수를 가지는 두 스티커 (100과 70)은 변을 공유하기 때문에, 동시에 뗄 수 없다.🐘 입력
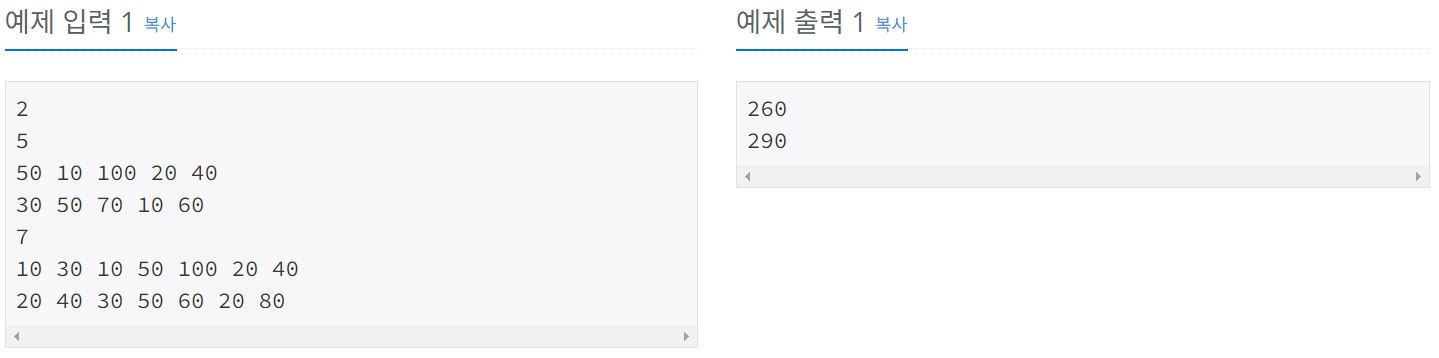
첫째 줄에 테스트 케이스의 개수 T가 주어진다.
각 테스트 케이스의 첫째 줄에는 n (1 ≤ n ≤ 100,000)이 주어진다.
다음 두 줄에는 n개의 정수가 주어지며, 각 정수는 그 위치에 해당하는 스티커의 점수이다.
연속하는 두 정수 사이에는 빈 칸이 하나 있다. 점수는 0보다 크거나 같고, 100보다 작거나 같은 정수이다.
🐥 출력
각 테스트 케이스 마다, 2n개의 스티커 중에서 두 변을 공유하지 않는 스티커 점수의 최댓값을 출력한다.
🦦 풀이
DP 문제는 언제나 해결 방안을 구하기 어려워서 좀 더 열심히 해야할 것 같다.
기본적으로 다이나믹 프로그래밍 에는 두가지 방법이 있다.
- Top-down
- Bottom-up
해당 문제에서는 1. Top-Down 방식으로 접근하고자 하였다.
또한 해당문제에서 생각해야 할 점은 현재 스티커를 떼어내면 상, 하, 좌, 우 스티커가 찢어지기 때문에 이 문제를 어떻게 접근할지 고민하게 되었다.
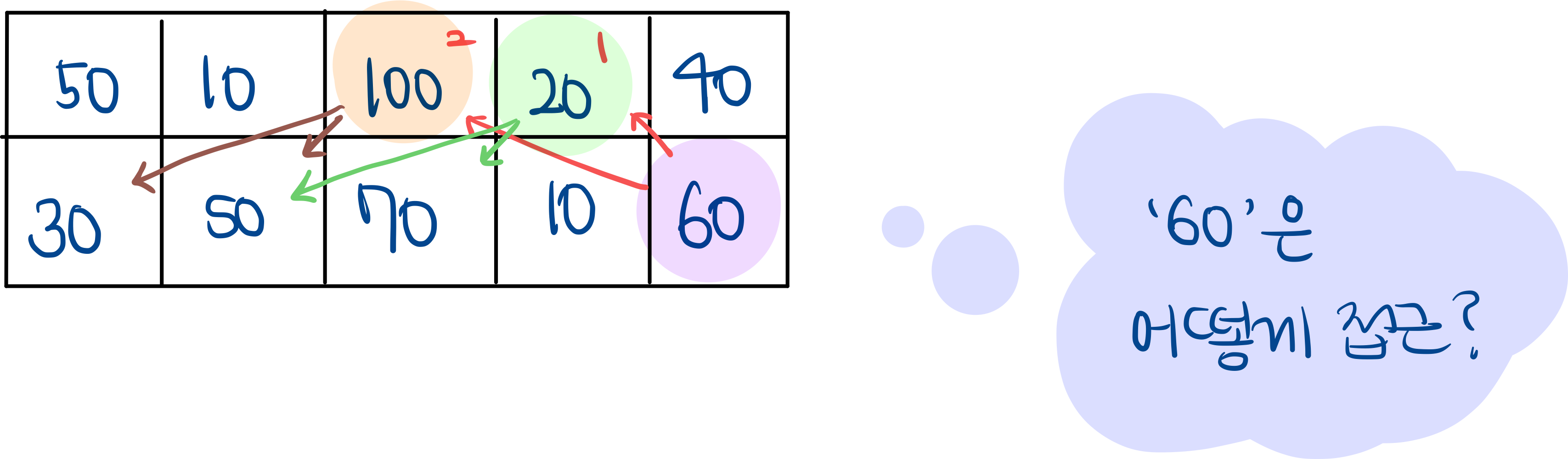
마지막열의 값인 40 과 60 이 만들어지려면 어떻게 해야할지 생각해보았다.
60 의 경우 바로 직전의 대각선인 20(1) 혹은 그 이전의 대각선 100(2) 을 통해서만 접근할 수 있다.
→ 문제의 조건을 보면 상, 하, 좌, 우는 찢어진다고 명시되어 있으므로!
즉 떼어내려는 스티커까지의 최대 cost 를 구하기 위해서는 직전 혹은 이전의 대각선을 통해 구할 수 있다는 것이다.
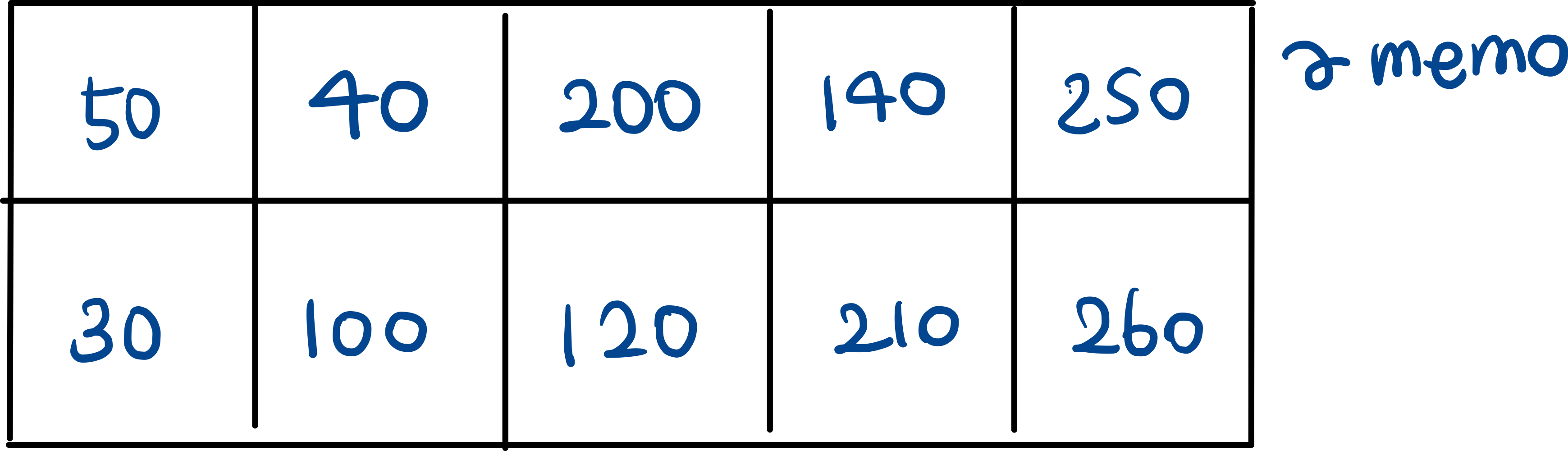
이를 활용하여 각 스티커까지의 최대 cost 값을 구한 memo 배열은 위와 같다.
예를 들어보자,
ary[0][2] = 200 인 (0, 2) 좌표의 값을 구하기 위해서는 (1, 0) 혹은 (1, 1) 좌표값에 의해 값이 결정되기 때문에
memo[0][2] = max(memo[1][0] + ary[0][2], memo[1][1] + ary[0][2]) 와 같이 구할 수 있고, 위의 방식대로 점화식을 구하면
1) i = 0
memo[i][j] = max(memo[1][j - 1] + ary[i][j], memo[i][j - 2] + ary[i][j])
2) i = 1
memo[i][j] = max(memo[0][j - 1] + ary[i][j], memo[0][j - 2] + ary[i][j])
와 같이 구할 수 있다.
🔔 코드
#include <iostream>
#include <vector>
using namespace std;
int main() {
int t_case;
cin >> t_case;
while(t_case--) {
int N;
cin >> N;
vector<vector<int>> ary(2, vector<int>(N, 0)), memo(2, vector<int>(N, 0));
// setting ary
for (int i = 0; i < 2; i++) {
for (int j = 0; j < N; j++) cin >> ary[i][j];
}
memo[0][0] = ary[0][0]; memo[1][0] = ary[1][0];
// "열" 을 기준으로 탐색
for (int i = 1; i < N; i++) {
if (i == 1) { // 1열인 경우
memo[0][i] = ary[1][i - 1] + ary[0][i];
memo[1][i] = ary[0][i - 1] + ary[1][i];
}
else {
memo[0][i] = max(memo[1][i - 1] + ary[0][i], memo[1][i - 2] + ary[0][i]); // 직전 대각선 vs 그 이전 대각선 중 max
memo[1][i] = max(memo[0][i - 1] + ary[1][i], memo[0][i - 2] + ary[1][i]); // 직전 대각선 vs 그 이전 대각선 중 max
}
}
int result_max = -1;
for (int i = 0; i < 2; i++) {
for (int j = 0; j < N; j++) result_max = max(memo[i][j], result_max);
}
cout << result_max << endl;
}
}💬 어려웠던 점
1. Top Down? Bottom Up?
→ 항상 DP 문제를 풀 때 memo 배열은 어떻게 구성해야하는지가 가장 어려운 것 같다.
점화식을 어떻게 작성해야하는지에 대한 연습이 필요한 것 같다.
