C++ 인접 행렬, 인접 리스트

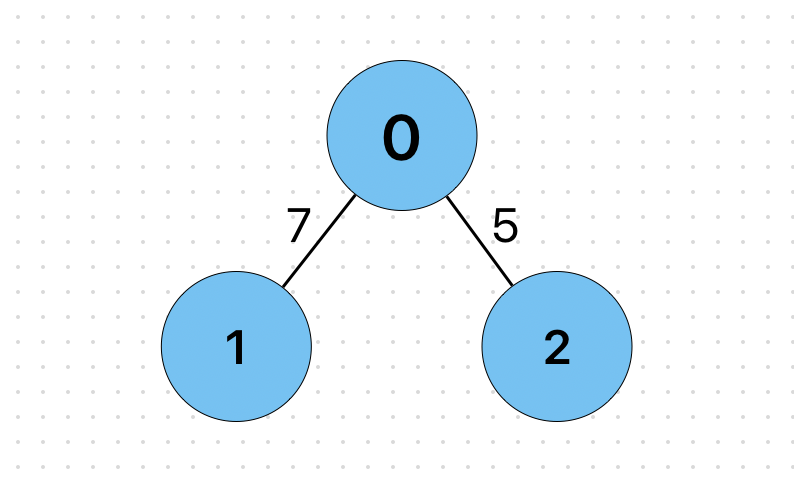
	0	1	2
0	0	7	5
1	7	0	무한
2	5	무한	0

그래프가 위와 같은 형태일 때, 인접 행렬과 인접 리스트 방식으로 표현해보자

인접 행렬

#include <bits/stdc++.h>
#define INF 999999999 // 무한의 비용 선언

using namespace std;

// 2차원 리스트를 이용해 인접 행렬 표현
int graph[3][3] = {
    {0, 7, 5},
    {7, 0, INF},
    {5, INF, 0}
};

int main(void) {
    // 그래프 출력
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
            cout << graph[i][j] << ' ';
        }
        cout << '\n';
    }
}

• 모든 관계를 저장하므로 노드 개수가 많을수록 메모리가 불필요하게 낭비됨

인접 리스트

#include <bits/stdc++.h>

using namespace std;

// 행(Row)이 3개인 인접 리스트 표현
vector<pair<int, int> > graph[3];

int main(void) {
    // 노드 0에 연결된 노드 정보 저장 {노드, 거리}
    graph[0].push_back({1, 7});
    graph[0].push_back({2, 5});

    // 노드 1에 연결된 노드 정보 저장 {노드, 거리}
    graph[1].push_back({0, 7});

    // 노드 2에 연결된 노드 정보 저장 {노드, 거리}
    graph[2].push_back({0, 5});

    // 그래프 출력
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < graph[i].size(); j++) {
            cout << '(' << graph[i][j].first << ',' << graph[i][j].second << ')' << ' ';
        }
        cout << '\n';
    } 
}

• 연결된 정보만을 저장하므로 메모리를 효율적으로 사용
• 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느림