인프런 js 알고리즘 공부를 하고 배운 내용을 정리한 게시글 입니다.
1.문제
멘토링
현수네 반 선생님은 반 학생들의 수학점수를 향상시키기 위해 멘토링 시스템을 만들려고 합니다.
멘토링은 멘토(도와주는 학생)와 멘티(도움을 받는 학생)가 한 짝이 되어 멘토가 멘티의 수학공부를 도와주는 것입니다.
선생님은 M번의 수학테스트 등수를 가지고 멘토와 멘티를 정합니다.
만약 A학생이 멘토이고, B학생이 멘티가 되는 짝이 되었다면, A학생은 M번의 수학테스트에서 모두 B학생보다 등수가 앞서야 합니다.
M번의 수학성적이 주어지면 멘토와 멘티가 되는 짝을 만들 수 있는 경우가 총 몇 가지 인지 출력하는 프로그램을 작성하세요.
입력문제
첫 번째 줄에 반 학생 수 N(1<=N<=20)과 M(1<=M<=10)이 주어진다.
두 번째 줄부터 M개의 줄에 걸쳐 수학테스트 결과가 학생번호로 주어진다. 학생번호가 제일
앞에서부터 1등, 2등, ...N등 순으로 표현된다.
만약 한 줄에 N=4이고, 테스트 결과가 3 1 4 2로 입력되었다면 3번 학생이 1등, 1번 학생이
2등, 4번 학생이 3등, 2번 학생이 4등을 의미합니다.
코드
function sol(test) {
let answer = 0;
let m = test.length,
n = test[0].length;
for (let i = 1; i <= n; i++) {
for (let j = 1; j <= n; j++) {
let cnt = 0;
for (let k = 0; k < m; k++) {
let pi = (pj = 0);
for (let s = 0; s <= n; s++) {
if (test[k][s] === i) pi = s;
if (test[k][s] === j) pj = s;
}
if (pi < pj) cnt++;
}
//여기 부분이 이해가 잘 안갔지만 , 노트로 정리해보니 모든 시험에서 ex (4,2) 의 경우수가 모든 시험에서 3번 이겨야지 멘토 멘티가 될수있기에 cnt 가 3일 되는경우가
//모든 시험에서 등수가 높은거기 때문이다.
if (cnt === m) answer++;
}
}
return answer;
}
let arr = [
[3, 4, 1, 2],
[4, 3, 2, 1],
[3, 1, 4, 2],
];
console.log(sol(arr));풀이
멘토링이라는 문제가 블루투포스 완전 탐색에 가장 대표적인 문제라고 한다.
사전에 이러한 모든 경우의 수를 구해서 하나씩 제거 하는 문제를 재귀함수 공부하면서 풀었던 적이 있었는데 이번 멘토링 문제는 문제 자체를 이해하는데도 오래 걸렸고 , 굉장히 어려운 문제였던거 같다.
그래도 풀이는 해야지,,,

모든 경우의 수를 구하기 위해서 i와 j를 for 문 돌렸다
해석 하자면 ,
| i | j |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
i와 j의 경우의 수는 1,1/ 1,2/ 1,3/ 1,4/ 2,1/2,2/2,3/2,4 ..... 해서 4,4 로 끝날것이다 . 1,1 2,2 3,3 4,4 는 있을 수 없는거기 때문에 나중에 없애주면 모든 테스트의 모든 경우의 수가 나올것이다.
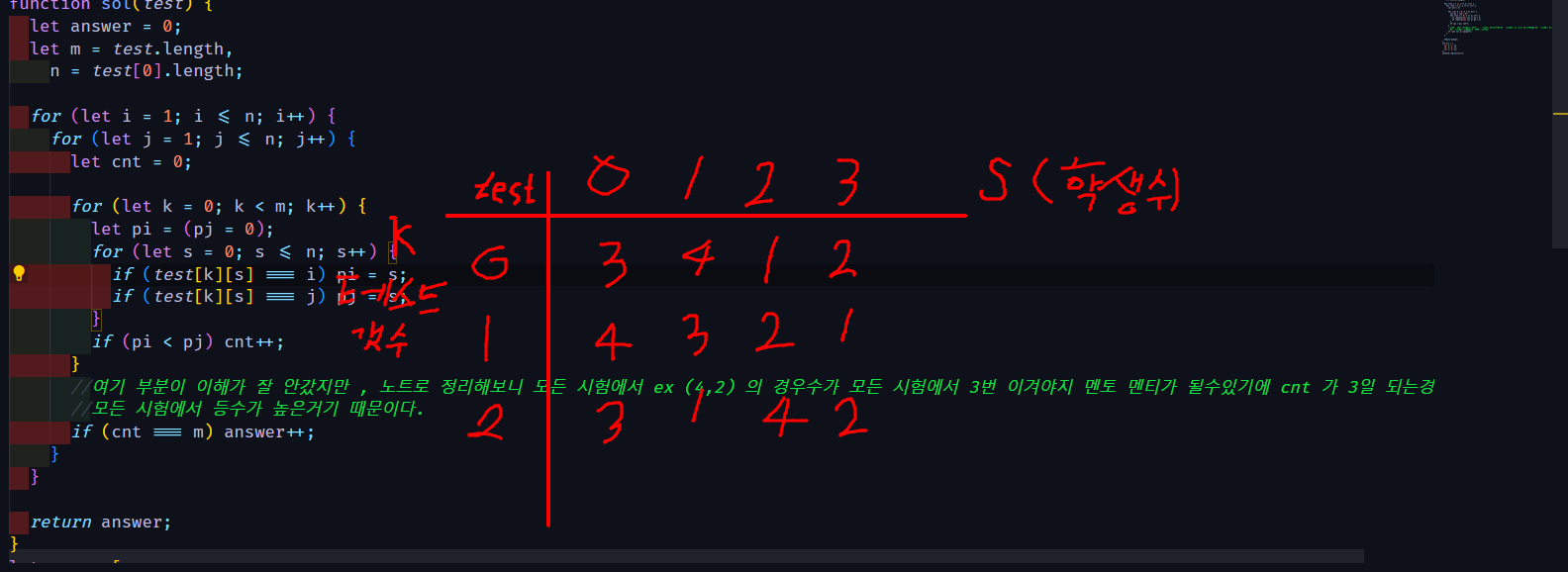
만약 (3,1)을 비교하교 있을때로 가정해보자.
test[k][s] === i 일때 k=0 번째일땐 3번은 0에 있다. pi라는 변수에 s를 할당해준다. 이 과정이 바로 멘티 멘토의 경우의 수가 되는지를 보는 과정이다.
이해가 잘 안되는 분들을 위해 예시를 가져와봤다.
(1,2) 라는 멘티 멘토가 되는 경우의수를 가져왔다.
k= 0 일때는 학생 1은 3등 학생 2는 4등이다.
이 조건에서는 pi < pj 가 성립된다.
k=1일때는 학생 1은 4등 학생 2는 3등
이 조건에서는 pi < pj 가 성립되지 않으므로 cnt 가 증가되지 않는다.
k=2일때는 학생1은 2등 학생 2는 4등
이 조건에서도 pi < pj가 성립되지만 k=1일때 학생 2가 학생 1보다 등수가 높았기 때문에 (1,2)의 경우의 수는 멘티 멘토가 될수없다.
모든 시험에서 등수가 높은 멘티 멘토 경우의 수가 나오면 cnt=3 이 되기 때문에 k for문이 끝난 이후에 cnt 가 시험수와 같다면 === m(모든 시험에서 등수가 높았던 경우)에만 answer 을 카운팅 해줌으로써 멘티 멘토의 경우의 수를 찾을 수 있다.
느낀점: 해당 문제를 접하고 풀어보고 해설도 보고 시간이 굉장히 오래걸린 문제다. 4중 for문을 돌리게 되면서 데이터가 어떻게 돌아가는지 이해하는데 오래 걸렸고 직접 큐스택을 그려서 넣어보면서 for문이 끝나고 조건문을 어디다 걸어야 하는지도 많이 헷갈렸다 . 점점 어려운 문제를 접하면서 드는 생각이 이렇게 풀면서 알고리즘 실력이 올라갈까 ? 라는 의문이 들지만 내가 뛰어난 사람도 아니고 그냥 성실히 풀다보면 언젠가 아는 문제가 나와서 하나라도 더 맞추지 않을까 ? 라는 생각으로 풀어야겠다.
