DFS 및 BFS의 코드들은 아래 주소에서 볼 수 있다.
https://github.com/HiiWee/algorithm-Java/blob/master/src/structure/Graph.java
백준 문제를 풀어가면서 자료구조를 공부하던 중 드디어 만난 BFS, DFS를 정리해보자
사실 BFS, DFS의 대략적인 원리는 알고 있었고 이를 이용한 문제는 여러번 풀어봤다. (프로그래머스, 백준 등)
이번 백준 1260 문제는 그래프 구조에서의 DFS, BFS풀이 방법이며, 정확한 자료구조와 알고리즘의 사용법을 알고있어야 풀이가 가능한 문제였다.
오늘은 DFS에 대해 알아보자!
그래프의 순회(탐색)
한 정점에서 시작하여 그래프에 있는 모든 정점을 한 번씩 방문하는 것을 말한다.
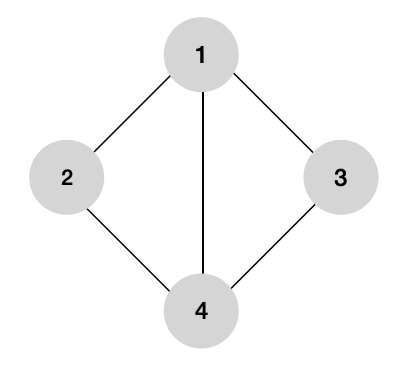
위와 같은 그래프는 정점 1, 2, 3, 4를 가지며 각각의 간선들은 방향성이 없는 무방향 그래프다.
위의 그래프를 순회하는 방법은 아래와 같이 매우 다양한 방법이 존재한다.
- 1 - 2 - 4 - 3
- 1 - 3 - 4 - 2
- 1 - 4 - 2 - 3
. . .
이런 순회에 하나의 규칙을 담아서 정의한 방법들 중 가장 많이 사용되는 방법들은
깊이 우선 탐색(Depth First Search), 너비 우선 탐색(Breadth First Search)가 대표적으로 존재한다.
두 개념은 어디서든 빠지지 않는 매우 대표적이고 중요한 알고리즘이며 꼭 익혀두어야 한다.
DFS
깊이 우선 탐색(Depth First Search)이다.
이름 그대로 좌우의 너비가 아닌 깊이를 우선적으로 탐색하는 방식이다.
각 노드의 탐색 방법은 아래와 같다.
- 시작 정점인
루트노드(R)을 결정하고 방문한다. 루트노드(R)의인접노드들을 스택에 담는다.- 스택에서 노드 하나를 꺼낸다.(R 노드의 인접노드들 중 하나가 된다.)
- 꺼낸 노드의 인접노드들을 스택에 담는다.
- 이후 꺼낸 노드의 데이터를 출력한다.
- 위 과정을 반복하고 더 이상 방문할 노드가 존재하지 않으면 탐색이 종료된다.
위 과정은 말로 설명하기 보다 그림으로 직접 설명하는것이 이해하기 수월하다.
위의 그래프 그림과 스택을 이용하여 순회 과정을 살펴보자
루트노트 =
1, DFS 탐색
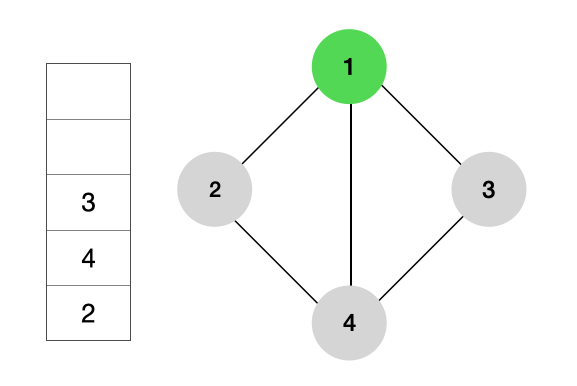
그래프의 첫 방문은 루트노드인 1의 인접노드(2, 3, 4)들이 좌측부터 순서대로 스택에 담기게 된다.
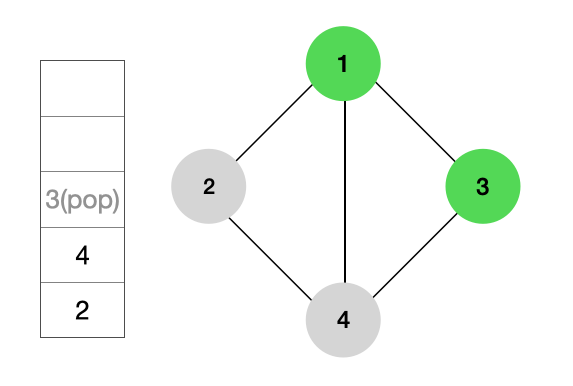
다음 노드를 탐색하기 위해 스택에서 POP을 하게 되면 마지막으로 삽입한 노드인 3이 꺼내지고, 3을 출력한다.
이때 추가적으로 아직 스택에 삽입하지 않은 노드를 삽입하게 되는데 3과 인접한 노드인 4는 이미 스택에 담겼으므로 출력만하고 다음 노드를 탐색한다.
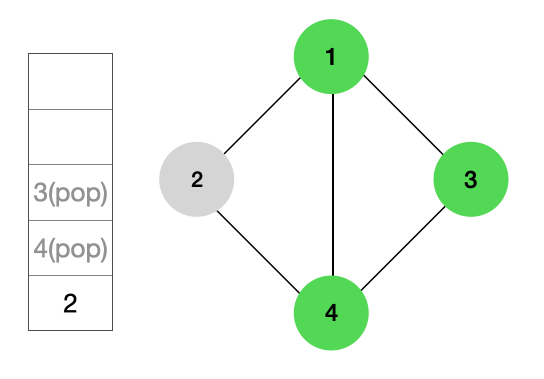
다음으로 스택에서 POP을 하게 되면 4노드가 꺼내지고 인접노드인 2가 스택에 이미 담겨있으므로 출력을 하고 다음 노드를 탐색한다.
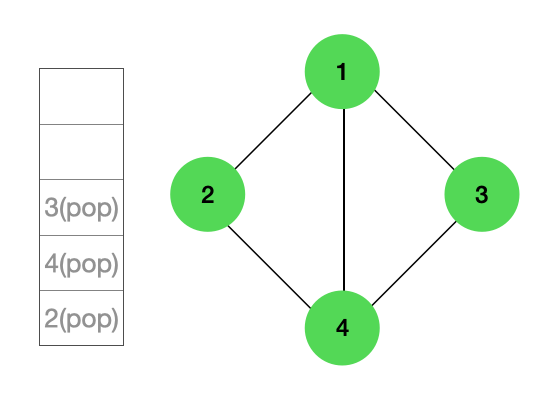
다음으로 스택에서 POP을 하게 되면 2가 꺼내진다. 인접 노드들은 이미 방문했기 때문에 다음 노드를 탐색한다.
하지만 스택이 비어있으므로 DFS가 종료된다.
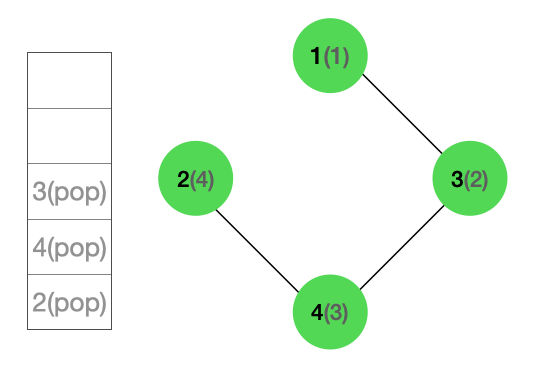
최종적인 순회 결과는 위와 같다. 괄호안에 숫자는 탐색한 순서를 나타낸다.
위의 결과를 코드로 구현해보자
DFS 구현(Java)
그래프는 인접행렬로 구현하는 방법과, 인접 리스트를 이용한 구현 방법이 존재하는데, 인접 리스트를 이용해 구현한 그래프를 알아보자
Graph, Node 클래스
인접 리스트를 이용한 그래프의 표현
Graph 클래스: 그래프를 구성하는 노드들을 저장하는 클래스
Node 클래스: 각 노드들의 데이터와, 인접리스트, 해당 노드의 방문여부를를 저장하는 클래스
data: 간단하게 int 타입을 이용adjacent(인접리스트): java.util.LinkedListvisited: boolean
public class Graph {
static class Node {
int data;
LinkedList<Node> adjacent;
boolean visited;
public Node(int data) {
this.data = data;
this.visited = false;
adjacent = new LinkedList<>();
}
}
Node[] nodes;
public Graph(int size) {
nodes = new Node[size];
for (int i = 0; i < size; i++) {
nodes[i] = new Node(i);
}
}
}Node 클래스
각 노드들을 관리하는 클래스이며
각 노드들이 생성될 때 생성자를 통한 모든 필드의 초기화 작업이 이루어진다.
Graph 클래스
Node클래스의 집합으로 이루어지며 생성자의 인수로 노드의 개수를 입력받는다.
이후 Node의 생성자를 이용해 모든 노드를 초기값으로 변경해준다.
편의를 위해 각 노드의 번호와 데이터 값은 동일하다.
Graph 클래스의 메소드
addEdge(int l1, int l2)
public void addEdge(int l1, int l2) {
Node n1 = nodes[l1];
Node n2 = nodes[l2];
if (!n1.adjacent.contains(n2)) {
n1.adjacent.add(n2);
}
if (!n2.adjacent.contains(n1)) {
n2.adjacent.add(n1);
}
}
// 콘솔에 현재 노드의 데이터를 출력
public void print(Node node) {
System.out.print(node.data + " ");
}노드 생성이후 각 노드들을 이어주는 간선을 추가해 각 노드들의 인접한 관계를 표시해준다.
List<T>.contains(Object T) 메소드는 리스트내에 동일한 요소가 있으면 참 값을 반환한다. !를 이용해 현재 리스트에 없는 노드만 추가해 중복을 방지한다.
현재 무방향 그래프를 만들고 있으므로 E(1, 2)와 E(2, 1)은 동일한 간선으로 취급된다.
DFS(int index) - 스택 이용
// 기본적인 DFS
public void DFS(int index) {
Node root = nodes[index];
Stack<Node> stack = new Stack<>();
stack.push(root);
root.visited = true;
while (!stack.isEmpty()) {
Node node = stack.pop();
for (Node n : node.adjacent) {
if (!n.visited) {
n.visited = true;
stack.push(n);
}
}
print(node);
}
}
매개변수로 받은 시작노드의 인덱스 값을 루트노드로 두고 스택을 하나 생성, 루트 노드를 PUSH및 방문처리를 한 이후 탐색이 시작된다.
기본적으로 스택은 모든 노드를 방문하기전까진 비어있지 않으므로(위의 그림 예시) while문의 종료조건은 스택이 비어있는 경우까지다.
- 스택에서 노드를 하나 꺼내고
- Node의 필드인
adjacent리스트에서 인접 노드들을 모두 스택에 담는다. - 스택에 담은 노드들은 모두 방문처리를 한다.
- 하나의 for문이 끝나면 인접노드들을 모두 방문했으므로 root노드의 데이터를 출력한다.
위의 작업 반복 언제까지? 모든 노드를 방문할 때까지
recursiveDFS(int index 혹은 Node root) - 재귀이용
// 재귀를 이용한 DFS
public void recursiveDFS(Node root) {
if (root == null) {
return;
}
print(root);
root.visited = true;
for (Node n : root.adjacent) {
if (!n.visited) {
recursiveDFS(n);
}
}
}
public void recursiveDFS(int index) {
Node root = nodes[index];
recursiveDFS(root);
}DFS는 BFS와 달리 노드와 방문하지 않은 인접한 노드가 없을때까지 계속해서 인접노드의 인접노드의 인접노드들을 파고들어가는 형식이므로(깊이 우선) 재귀함수를 이용할 수 있다.
우선 Node root를 인자로 받은 후 root가 null값을 갖지 않는다면 탐색을 시작한다.
기존 스택을 이용한 DFS와의 차이점은 현재 데이터를 먼저 출력하고 인접리스트의 순서대로 탐색을 시작하는데 스택을 이용한 방식과 탐색 순서의 차이가 존재한다.
스택이용 DFS는 스택에 해당 노드의 인접리스트의 값을 모두 담고 현재 데이터를 출력한다.
스택은Last In First Out의 구조로 마지막으로 삽입한 인접노드가 가장 먼저 출력된다. 즉, 각 노드의인접리스트(adjacent)에 저장된 역순서로 탐색한다.
(위의 그림을 이용한 설명에서의 방식)
재귀이용 DFS는 데이터를 출력하고 탐색을 시작하므로 인접리스트의 순서 그대로 탐색하게 된다.
[알고가자]
탐색순서라는 것은 어떤 간선을 먼저 추가해줬냐에 따라 달리지게 되므로 만약 인접리스트의 탐색순서를 데이터의 값이 작은 순 혹은, 노드 번호가 작은 순서로 탐색해야 한다면 정렬을 이용한 후 탐색하는 것이 좋다.
main함수 및 실행결과
public static void main(String[] args) {
Graph graph = new Graph(4);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(0, 3);
graph.addEdge(2, 3);
graph.addEdge(1, 3);
// 스택이용 DFS
graph.DFS(0);
System.out.println(); // 개행
graph.init(); // 방문 노드값 초기화
// 재귀이용 DFS
graph.recurDFS(0);
System.out.println(); // 개행
}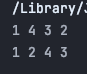
초기에 그림으로 설명한 그래프를 이용해 간선을 추가하고 스택을 이용한 DFS와 재귀함수를 이용한 DFS는 탐색하는 순서가 다름을 알 수 있다.
(탐색하는 순서는 다르지만 깊이를 우선적으로 탐색하는것은 동일하다!)
결론
논리적인 이해와 그것을 실제 코드로 구현하는 것은 많은 차이가 있었다.
단순히 논리적 판단으로 넘어가던 것도 실제 코드레벨에서는 명확하게 작성해줘야 하는것에 어려움을 느꼈다.
지금껏 Problem Solving을 하면서 느낀것은 기초적인 알고리즘을 매우 잘 익혀놔야 응용된 문제가 나와도 쉽게 적용할 수 있다는 점이다.
오늘 설명한 DFS는 매우 중요한 탐색 알고리즘이다.
그래프 뿐만아니라 배열, 트리 등 다양한 구조의 탐색에도 사용되며 굉장히 많이 사용되는 알고리즘이므로 동작원리를 잘 이해하고 있는것이 중요하다.
ps - DFS는 다른 수많은 사람들이 정리한 블로그 글이 있지만, 만약 이 글을 보고 있는 사람이 있다면 온전히 자신의 생각으로 글을 정리해서 써보길 추천한다. 얻는것이 훨씬 크고 깊을 것 입니다. 장담해요!!
좀 더 노력하자 할 수 있다!

