📕 오늘 배운 내용!
- 트리 (Tree)
- 이진 탐색 트리 (Binary Search Tree)
- 그래프 (Graph)
✏️ 트리 (Tree)
-
하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무를 거꾸로 뒤집어 놓은 듯한 형태
(단방향 그래프의 한 구조) ➜ 사이클이 없음
( 루트(나무의 뿌리)를 시작으로 여러개의 데이터를 간선(edge)(나무의 가지들)으로 연결 ) -
계층적 자료구조 ➜ 한 데이터가 바로 아래에 있는 하나 이상의 데이터에 무방향으로 연결되어 있음
-
두 개의 노드가 상하 계층으로 연결되면 부모/자식 관계
-
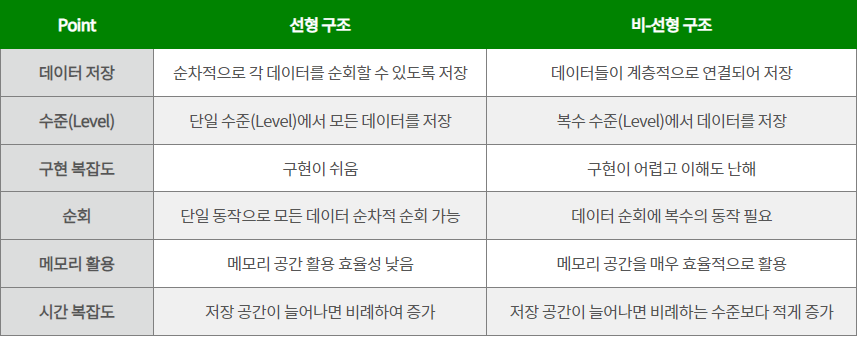
비선형 구조 ➜ 하나의 데이터 아래에 여러 개의 데이터가 존재
💡 선형 구조와 비선형 구조의 차이
✔ 트리 구현 메서드
addChildNode(value)- 입력받은 value를 Tree에 계층적으로 추가
⠀removeChildNode(node)- 입력받은 node를 Tree에서 삭제
⠀getChildrenNode()- 현재 트리에서 존재하는 children을 리턴
⠀contains(value)- 트리에 포함된 데이터가 있는지를 Boolean 타입으로 리턴
- 깊이, 높이, 레벨 등 측정
✔ 깊이 (depth)
- 루트로부터 하위 계층의 특정 노드까지의 깊이(depth)
- 루트(맨위)는 깊이가 0이고 밑으로 한 레벨씩 내려갈 수록 깊이 1증가
✔ 레벨(Level)
- 트리 구조에서 같은 깊이를 가지고 있는 노드를 레벨(level)로 표현가능
- 루트(맨위)부터 레벨1, 깊이가 내려갈 수록 레벨2,3,4 ..로 증가
✔ 높이(Height)
- 리프 노드(각 노드의 맨 아래)를 기준으로 루트까지의 높이(height)를 표현 가능
- 부모 노드 높이 = 자식 노드의 가장 높은 height 값 + 1
- 리프 노드의 높이는 0이고 위로 한 레벨씩 올라갈 수록 높이 1 증가
⠀
Ex. 대표적으로 파일(디렉토리) 구조, 월드컵 토너먼트 대진표, 족보, 회사의 조직도 등
( 폴더는 하나의 폴더(루트 폴더, /)에서 시작되어, 가지를 뻗어나가는 모양새 )
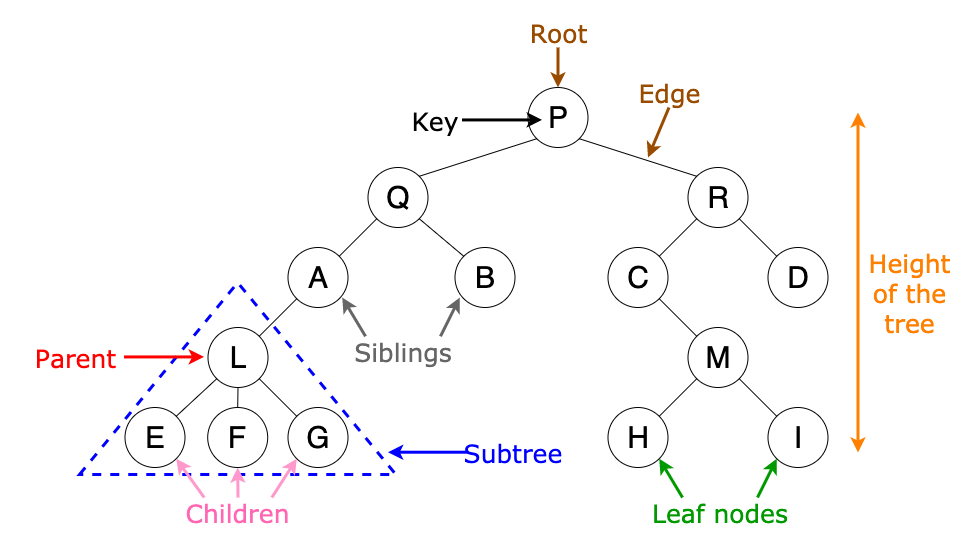
✔️ 용어
노드(Node)- 트리 구조를 이루는 모든 개별 데이터루트(Root)- 트리 구조의 시작점이 되는 노드 (맨 위 노드)리프(Leaf)- 트리 구조의 끝 지점, 자식 노드가 없는 노드 (맨 아래 노드)부모 노드(Parent node)- 두 노드가 상하관계로 연결되어 있을 때, 상대적으로 루트에서 가까운 노드
( 상하관계 중 상위 노드 )자식 노드(Child node)- 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
( 상하관계 중 하위 노드 )형제 노드(Sibling Node)- 같은 레벨에 나란히 있는 노드서브 트리(Sub tree)- root에서 뻗어 나오는 큰 트리의 내부에, 트리 구조를 갖춘 작은 트리
✏️ 이진 트리 (Binary Tree)
-
자식 노드가 최대 두 개인 노드들로 구성된 트리 ( 왼쪽 자식 노드 / 오른쪽 자식 노드로 구분 )
-
이진 탐색 트리와 다르게 노드간의 대소관계는 신경 X
-
자료의 삽입, 삭제 방법에 따라 정 이진 트리(Full binary tree), 완전 이진 트리(Complete binary tree), 포화 이진 트리(Perfect binary tree)로 나뉨
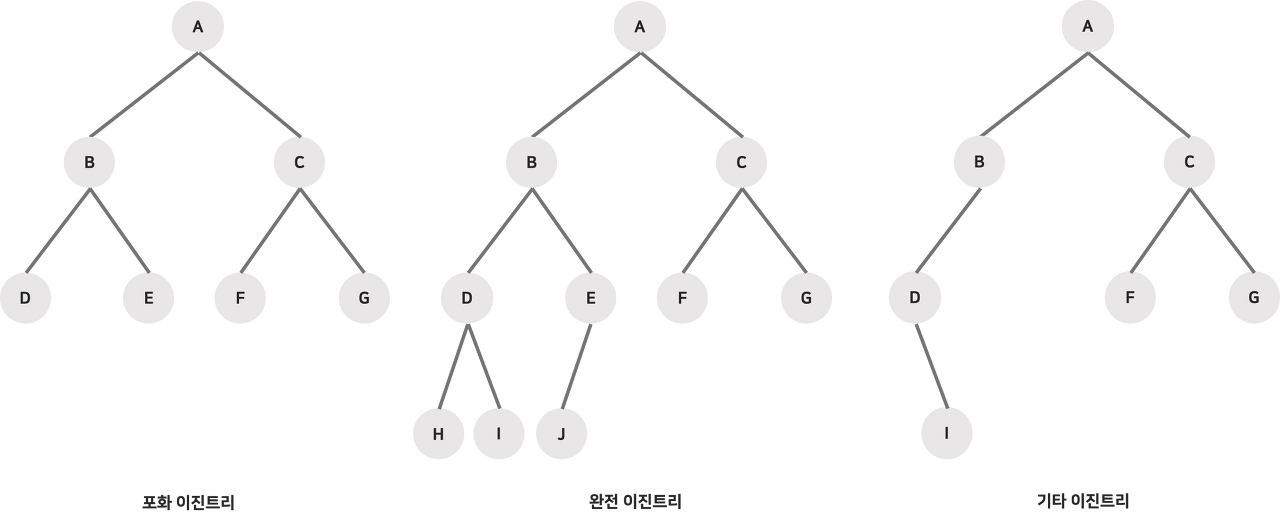
✔ 정 이진 트리 (Full binary tree)
➜ 자식 노드가 아예 없거나, 최대 둘뿐인 트리 ( 자식을 하나만 가진 노드가 없어야 함 )
✔ 완전 이진 트리 (Complete binary tree)
➜ 마지막 레벨을 제외한 모든 서브트리의 레벨이 같고, 마지막 레벨은 전부 차 있지 않아도 되지만 왼쪽부터 채워져 있어야 하는 트리
✔ 포화 이진 트리 (Perfect binary tree)
➜ 모든 리프 노드의 레벨이 같고, 빈공간 없이 모든 노드가 2개의 자식을 갖고있는 트리 ( 완벽한 피라미드 형태 )
➜ 정 이진 트리이면서 완전 이진 트리인 경우
높이가 h 일때 최대 노드의 수는 2^(h+1) -1 개이다 이때 이진트리에서 최대 노드의 수를 만족하는 트리를 포화 이진트리라 한다 (ex - 높이가 3인경우 최대 노드 수 : 2^6 - 1 = 15)
✏️ 이진 탐색 트리(Binary Search Tree)
-
탐색을 위한 이진 트리
-
모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가짐
✏️ 그래프 (Graph)
-
여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조 (복잡한 네트워크망)
-
직접적인 관계의 경우, 두 점 사이를 이어주는 선이 있음
-
간접적인 관계의 경우, 몇 개의 점과 선에 걸쳐 이어짐
( 트리도 그래프의 한 종류 )
- 배열과 다르게 index가 0부터 존재
✔ 그래프 구현 메서드
Arrays.deepToString()- 다차원 배열(배열이 또 다른 배열을 요소로 가지고 있는 배열)을 String으로 변환 ➜ 2차원 배열의 값을 출력하기 좋음
( 2차원 배열 = 1개의 배열 안에 요소로서 다른 배열을 가지고 있는 형태 )
⠀setGraph(size)- 그래프에 size만큼의 버텍스 추가
⠀getGraph()- 인접 행렬 정보가 담긴 배열 반환
⠀addEdge(from, to)- fromVertex와 toVertex 사이 간선 추가
⠀addEdge(개수)- 정점 추가
⠀hasEdge(from, to)- fromVertex와 toVertex 사이의 간선이 존재하는지 여부 Boolean으로 반환 (있으면 true / 없으면 false)
⠀removeEdge(from, to)- fromVertex와 toVertex 사이 간선 삭제
✔ 그래프 표현 방법
1. 인접 행렬
- 서로 다른 정점들이 인접한 상태인지를 표시한 행렬 ( 인접하면 1(true), 아니면 0(false) )
- 2차원 배열 matrix의 형태로 나타냄
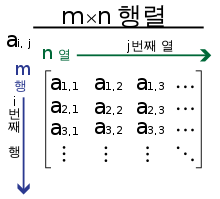
Ex.
matrix[v][w] = 1 : 정점 v에서 정점 w로 가는 간선이 있음
matrix[v][w] = 0 : 정점 v에서 정점 w로 가는 간선이 없음
matrix.length (matrix 행의 길이) = matrix[i].length (matrix i행의 열(요소들)의 길이)
✔️ 인접 행렬이 사용되는 경우
- 두 정점 사이에 관계가 있는지, 없는지 확인
Ex. A에서 B로 진출하는 간선이 있는지 파악하기 위해 ➜ 0 번째 줄의 1 번째 열에 어떤 값이 저장되어있는지 바로 확인 가능- 가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용
- 무방향 그래프 ⬇️
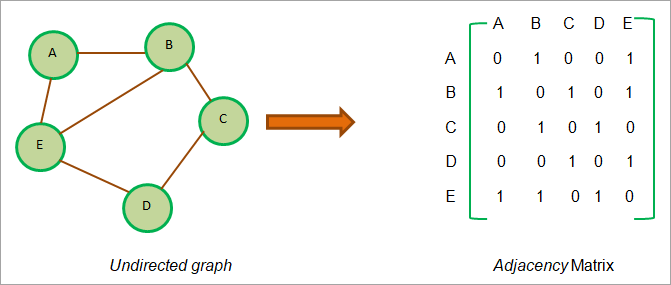
- 방향 그래프 / 비가중치 그래프 ⬇️
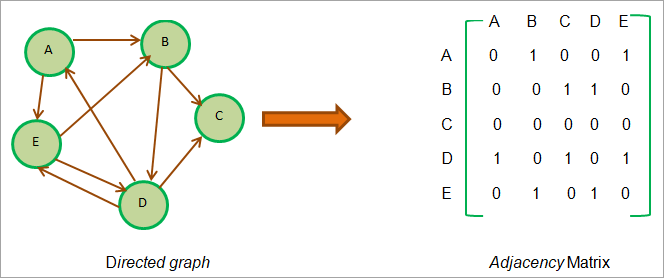
- 가중치 그래프 ⬇️
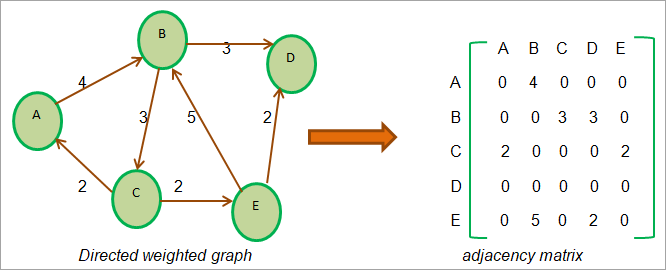
2. 인접 리스트
- 각 정점이 어떤 정점과 인접하는지를 리스트의 형태로 표현
- 각 정점마다 하나의 리스트 가지고 있음 ( 이 리스트는 자신과 인접한 다른 정점을 담고 있음 )
✔️ 인접 리스트가 사용되는 경우
- 메모리를 효율적으로 사용하고 싶을 때 사용
( 인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리 많이 차지 )
- 무방향 그래프 ⬇️
( 특정 노드에 대한 모든 인접 노드를 순회했을 때, 인접 목록의 마지막 노드의 다음 포인터 필드에 NULL을 저장 )
➜ 인접 목록의 총 길이 = 그래프 간선 수의 두 배
( 아래 그래프에서 간선의 총 개수 = 6개, 인접 목록의 길이의 합 = 12 )
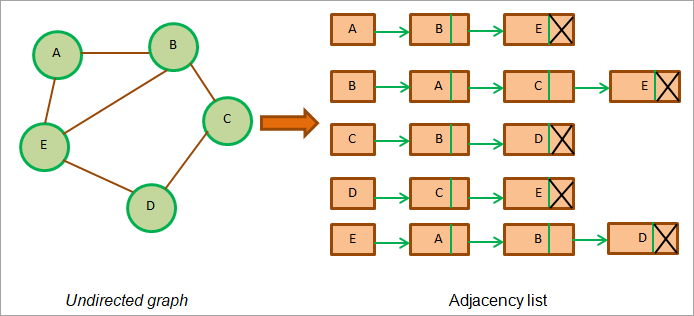
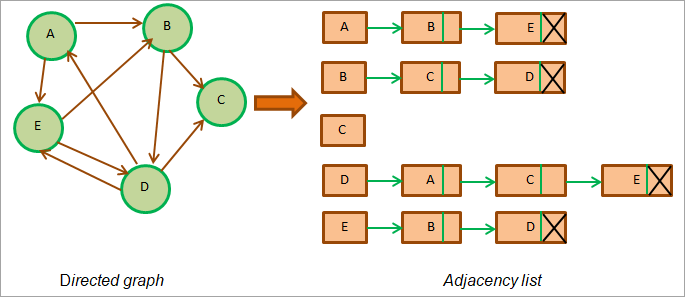
- 방향 그래프 / 비가중치 그래프 ⬇️
➜ 인접 목록의 총 길이 = 그래프의 간선 수
( 아래 그래프에서 간선의 총 개수 = 9개, 인접 목록 길이의 합 = 9 )
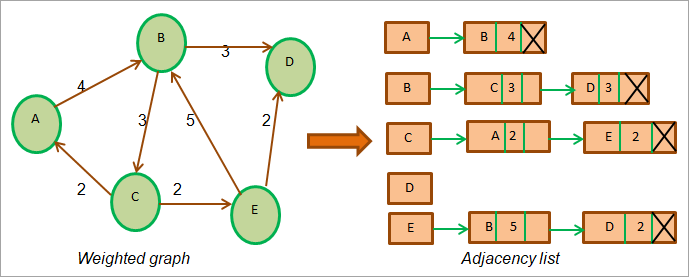
- 가중치 그래프 ⬇️
( 가장자리의 가중치를 나타내는 새 필드를 각 목록 노드에 추가해야 함 )
✔️ 용어
정점 (vertex)- 데이터가 저장되는 그래프의 기본 원소 ( 노드(node) )간선 (edge)- 정점을 이어주는 선인접 정점 (adjacent vertex)- 하나의 정점에서 간선으로 직접 연결되어 있는 정점가중치 그래프 (weighted Graph)- 연결의 강도(추가적인 정보)가 얼마나 되는지 적혀져 있는 그래프비가중치 그래프 (unweighted Graph)- 연결의 강도가 적혀져 있지 않는 그래프무방향 그래프 (undirected graph)- 모든 간선이 방향이 없이 표현되어있는 그래프 ( 각 정점이 왔다갔다 가능 )
Ex. 정점 v와 정점 w를 연결하는 간선을 (v, w)라고 하면, (v, w)와 (w, v)는 같은 간선.
정점 n개일 때 무방향 그래프가 가질 수 있는 최대 간선 수는 n(n-1)/2개방향 그래프 (directed graph)- 모든 간선이 방향이 표현되어 있는 그래프 ( 단방향으로만 진출 가능 )
Ex. 정점 v에서 w로 가는 간선을 (v, w)라고 하고, 이때는 간선 (w, v)와 다름.
정점 n개일 때 방향 그래프가 가질 수 있는 최대 간선 수는 n(n-1)개진입차수 (in-degree)/진출차수 (out-degree)- 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선이 몇 개인지인접 (adjacency)- 두 정점 간에 간선이 직접 이어져 있다면 이 두 정점은 인접한 정점자기 루프 (self loop): 정점에서 진출하는 간선이 다른 정점을 거치지 않고, 곧바로 자기 자신에게 진입하는 경우 ( 자기 루프를 가졌다 )사이클 (cycle)- 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있는 경우 (사이클이 존재하는 그래프 라고 함)
[참고] https://www.softwaretestinghelp.com/java-graph-tutorial/
🌈 느낀점
이번 학습은 Coplit 문제들에 집중하다가 시간이 없어 당일에 블로그를 작성하지 못했다ㅠ
그래도 주말에 복습하면서 다시 한번 개념을 이해했다!
하지만 Stack, Queue와 같이 막상 문제를 만나면 잘 응용하지 못할 것 같다..ㅠ
미리 풀어봐야지 ㅠㅠ