Chapter 1 Counting

1. Sets

• Sets and Subsets

• Empty Set (공집합)

• Union (합집합)

• Intersection (교집합)

• Complement (여집합)

• Disjoint Sets (서로소 집합)
  : Sets that do not have any overlap

• Partition
  : Imagine a set $A$, and then imagine subsets $A_1, A_2, \cdots, A_n$. If these subsets are disjoint (so they do not overlap) and cover all possible outcomes in A, they partition the set $A$

2. Naive Probability

Concept 1.1 Basic Definitions

• Sample Space
  : A sample space is the set of all possible outcomes of an experiment.

• Event
  : An event is a subset of the sample space.

• Naive Definition of Probability
  : The probability of an event occurring, if the all outcomes are equally likely in a finite sample space.

  $P(Event) = \frac{\#\; of\; Favorable\; Outcomes}{\#\; of\; Outcomes}$

Concept 1.2 Multiplication Rule

발생 가능한 경우의 수가 $n_1$, $n_2$, $n_3, \cdots, n_r$ 가지인 1, 2, 3, $\cdots$, $r$ 번의 시행에서 발생 가능한 모든 경우의 수는 $n_1\cdot n_2\cdot n_3 \cdots n_r$ 이다.

Example 1.

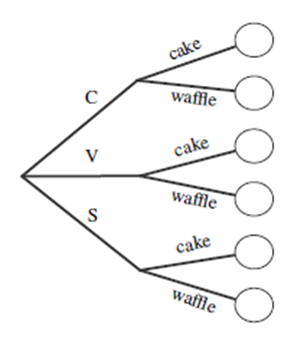
Concept 1.3 Factorial

Concept 1.4 Binomial Coefficient

The Binomial Coefficient gives the number of ways that $x$ objects can be chosen from a population of $n$ objects.

Sampling Table

	Order Matters	Order Doesn’t Matter
With Replacement	$n^k$	${n+k-1 \choose k} = {n+k-1 \choose n-1}$
Without Replacement	$\frac {n!}{(n-k)!}$	${n \choose k}$

with replacement, and order doesn’t matter

$n = 4,\; k = 6$
복원이며 순서 상관있다는 조건에서 $n$개중 $k$개 뽑는 경우의 수는 $k$개의 원소 사이에 $n-1$개의 구분자(Divider)를 배치하는 것 또는 $n+k-1$개의 자리에서 원소 $k$개의 자리를 정하는 경우의 수와 동일하다.

${n+k-1 \choose k} = {n+k-1 \choose n-1}$

원소의 위치를 먼저 정하면 구분자의 위치가 결정되고, 그 반대도 마찬가지다.

Story Proof

• Ex. 1 Symmetry of the Binomial Coefficient
  Choosing $k$ elements out of $n$ is the same as choosing $n-k$ elements out of $n$.
  ${n \choose k} = {n \choose n-k}$
• Ex. 2
  Imagine picking k people out of n, and then designating as president. You can either select all k people, and then choose 1 from among those k. Or, you can select a president, and then choose the remaining k-1 out of the n-1 people.
  $n \cdot {n-1 \choose k-1} = k \cdot {n \choose k}$

• Ex. 3 Vandermonde's identity
  Suppose you had $m$ boys and $n$ girls, and you needed to select $k$ children out of them all. You could do this by first choosing $j$ out of the $m$ boys, and then choosing $k-j$ of the girls. You would have to apply the multiplication rule to get the total number of combinations, and then sum them all up.
  ${m+n \choose k} = \sum_{j=0}^{k}{m \choose j}{n \choose k-j}$
  Since the events according to j are disjoint with each other, all of them can be added.

Symmetry

Example
Imagine a standard, well-shuffled, 52 card deck of cards. You are dealt four cards from the deck at random. On average, how many spades will you get in this four card deal?

Solution
Let’s use symmetry. we can think of there being 13 groups of 4 cards each in this deck (i.e., cards 1 through 4 are one group, then cards 5 through 8, etc.), and we simply own the first ‘group’ of 4 cards.

We know that the total number of spades totaled across all of these groups is always 13; there are 13 spades in the deck, and these 13 groups account for the entire deck.

By symmetry, we know that, on average, every group will get the same amount of spades. So, since there are 13 groups that represent 13 spades between them, and every group has the same average number of spades, each group must get 1 spade on average (it wouldn’t make sense if certain groups of 4 tended to get spades more often). So, in your four-card deal, you expect one spade.

Non-naïve Definition of Probability

Let $s$ be a sample space, the set of all possible outcomes of some experiment. $s$ might not be finite anymore, and all outcomes might not be equally probable, either.

• Axiom 1

  $P(\theta) = 0 \\ P(\Omega) = 1$

• Axiom 2

  $P(\bigcup_{n=1}^{\infty}A_n) = \sum_{n=1}^{\infty}P(A_n) \Leftrightarrow A_1, A_2, \dots, A_n \;are \;disjoint (non-overlapping)$