자료구조

빅오 표기법의 특징상수항을 무시하고 오직 가장 큰항만을 고려하여 표기한다. 그 이유는 데이터가 커질 수록 최고차항이외의 항이 가지는 연산의 의미는 감소하기 때문이다.Untitled위의 그림에 따르면 상수<로그<선형함수<다항함수<지수함수 순으로 시간

자료구조를 파이썬으로 공부하는데 파이썬 문법을 까먹어서 모르는 것만 정리s.append(item) - llist 뒤에 item 추가s.extend(lst) - list s 뒤에 다른 리스트인 lst 추가s.count(item) - s 리스트에서 항목 item의 개수를

스택 클래스후위 표기법 계산하는거 근데 이거 여기서 val2 랑 val1 순서 바꾸면 뺄샘 결과가 바뀐다 개같은거연산자 우선순위 반환하는 함수중위 표기법을 후위 표기법으로 전환하는 방법함수위 대표적인 알고리즘을 정리하면먼저 출력할 리스트와 연산자들을 쌓아둘 스택을 만

음 뭔가 잘안되던 부분책에서는 readline() 을 실행하면 파일 전체를 읽어온다고 되어 있는데 사실 이 함수 쓰면 한줄 씩 밖에 못읽는다그래서 read()를 전체를 한번에 읽고 lines.split(”\\n”)을 사용해서 한줄씩 읽어서 list를 생성한다음에 for

상속을 원하는 클래스를 import 한 후에 상속 받은 클래스를 생성하기 위해서 는 아래와 같이 자식클래스의 클래스명에 부모클래스 명을 넣어준디.class 자식 클래스 명(부모 클래스 명):위와 같이 작성하면 부모의 생성자 또한 호출되어서 자식클래스는 부모의 기능 +

self.list.pop(pos) 위의 코드에서 삭제를 진행할때 인덱스를 pos로 고정하고 날렸다

진은아 그냥 외워 어차피 너 이거 생각 못해for i in range(len(string)-1,0,-1): 진은아 문자열 반대로 출력할때 이렇게 안하면 ㅈ된다 문자열 총 길이에서 -1 해줘야 하는거야range() 사용하면 범위에서 제한되는 거여, range(a,b,c

위와 같은 display함수에서 self.front r가 self.rear보다 클 때 두 리스트를 시작점을 기준으로 리스트 슬라이싱 함수를 이용해서 두 리스트를 구하고 더해서 반환하는 과정을 할 때 self.front 가 리스트의 MAXQ보다 1작은 상황일때 self

BFS 너비 우선 탐색

오늘 태어나서 처음으로 게슈탈트 붕괴현상을 경험했다 이건 진짜 존나 오바참치적이게 될수도 있으니까 위에 함수 구현하는데 3시간동안 디버깅을 했는데 구현이 안되는거다 그 이유가 뭐였냐면 위에 코드에서self.isFull() 을 사용했는데 내가 저걸 그냥 ()를 안써서 계

위에 코드에서 가장 신경써야 하는 점은 dequeue 부분이다 stack은 max량이 없으니 enqueue는 계속해서 stack1 에 쌓는것이 가능하다 하지만 dequeue는 stack2가 비어 있으면 구현이 불가능하다 따라서 이를 수정해야 하는데 이를 위해서 if 문

시험보기 전에 한번씩 보고 시험에 임할것

문자열을 받아서 하나하나 덱에 순서대로 넣어준다 (덱 1에)그 다음에 deleteFront 를 실시해서 문자열 뒤에서 부터 꺼내서 다른덱에 넣어주고그 다음에 다른덱에서 deleteRear 을 실시해서 원래 문자열을 처음 넣어주었던 덱의 deleteRear한 문자열과 비

링크드 리스트연결된 구조로 되었있음노드로 구성되어 있는데 노드에는 링크필드와 데이터 필드가 있음링크필드 다른 노드들과 연결시켜주는 부분으로 다른 객체의 주소값이 들어있다.데이터 필드 저장하려는 데이터들이 위치하는 필드연결리스트는 용량이 고정되어있지 않다.데이터의 삽입과

삭제

삭제

파이썬 리스트에서는 삭제과 삽입을 실행할 때 각 항목들의 이동이 필요해서 시간복잡도가 O(n)이지만 연결 리스트를 사용한다면 삽입과 삭제의 시간복잡도는 O(1)이다. (링크만 수정하면 사용간능하기 때문이다.)연결된 리스트에서는 n번째 항목에 접근하는데 걸리는 시간은O(

리스트 내부의 요소를 선택 정렬하는 함수를 구현했다 기본적인 작동원리는 이중 포문안에서 돌아가는데 첫번째 원소를 기준으로 시작해서 돌아간다. 처음에 원소 하나a 를 시작으로 least값을 초기화 해준다 이후 이 least값 안에는 최솟값이 삽입될 것이다 이루 a +1

버블정렬은 앞뒤의 두개의 요소를 비교해서 교환하는 과정을 반복하는 방법이다 이 방법이 효휼적인 경우는 대부분의 원소가 정렬이 되었있을때이다 하지만 정렬이 되어있지 않는 경우에는 시간복잡도가 증가하는 방법이다.

이진탐색은 값의 탐색에 있어서 가장 빠르다는 장점을 가진다 그 이유는 시간복잡도에서 나오는데 이진탐색법으 시간복잡도는 log2 n을 가진다 이는 그 이유는 연산을 실행할 수록 탐색 대상이 반으로 줄어들기 때문이다.위의 이진탐색과 유일하게 다르점이 바로 미드를 설정하는

해싱이란 키 해싱 키값의 산술적인 연산을 통해서 인덱스를 계산하는 방법이다.해싱에서 킷값으로부터 레코드가 저장될 위치를 계산하는 함수를 해시함수계산된 위치에 레코드를 저장한 테이블을 해시태이블해시테이블이 충뿐히커서 몯 담을 수 있는 인덱스를 부여받는다면 탐색에 걸리는

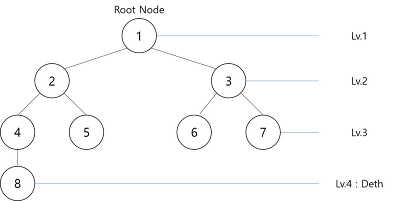
용어정리 헷갈리는 것만Untitled노드(Node) : 트리의 기본 요소. 자료 항목과 다른 항목에 대한 가지(Branch)를 합친 것이다.가지(Branch, Edge) : 노드와 노드를 연결하는 간선Root Node : 트리의 맨 위에 있는 노드이다. 위 예시에는 1

트리: 계층적인 관계를 가진 자료의 표현애 유용한 자료구조이진트리의 정의공집합이거나루트와 왼쪽 서브트리, 오른쪽 서브 트리로 구성된 노드들의 집합. 이진트리의 서브 트리들은 모두 이진트리이어야 함.포화이진트리 - 각 레벨의 노드가 가득찬 이진트리완전이진트리 - 각층의

삽입연산삽인 연산 알고리즘일단 들어온 정수 배열의 제일 끝에 넣어일단 self.size()함수를 이용해서 제일 끝의 인덱스를 얻는다반목문을 실행하는데 제일 첫노드가 아닐때 까지 그리고 self.parent(i) 보다 새로 들어온 정수가 클때 까지만 반복한다위 조건을 만

class minheap: def init(self): self.heap = [] self.heap.append(0) def size(self): return len(self.heap) - 1 def

모든 노드는 유일한 키를 갖는다왼쪽 서브 트리의 키들은 루트의 키보다 작다.오른쪽 서브트리의 키들은 루트의 키보다 크다.왼쪽과 오른쪽의 서브트리도 이진탐색트리이다.BSTnode class - 생성자로 key 값과 value 값을 받아서 초기화 함이진 탐색트리 생성탐색트

트리: 계층적인 관계를 가진 자료의 표현애 유용한 자료구조이진트리의 정의공집합이거나루트와 왼쪽 서브트리, 오른쪽 서브 트리로 구성된 노드들의 집합. 이진트리의 서브 트리들은 모두 이진트리이어야 함.포화이진트리 - 각 레벨의 노드가 가득찬 이진트리완전이진트리 - 각층의

높이를 각각 순환적을 계산하면 마지막에 총 차를 구할 수 없기때문에 함수를 두개로 나누어서 작성했다.

모든 노드는 유일한 키를 갖는다왼쪽 서브 트리의 키들은 루트의 키보다 작다.오른쪽 서브트리의 키들은 루트의 키보다 크다.왼쪽과 오른쪽의 서브트리도 이진탐색트리이다.BSTnode class - 생성자로 key 값과 value 값을 받아서 초기화 함이진 탐색트리 생성탐색트

그래프 G는 (V,E)로 표시간선(edge) 또는 링크(link): 정점들간의 관계의미undirectied graph: 무방향 그래프 - 그래프 vertex간의 방향성이 존재하지않는다(a,b) ==(b,a)directed graph : 그래프 vertex간의 link에

삽입 정렬의 정렬간격이 1인 것에 비해서 정렬의 간격이 gap만큼 벌어져있는 정렬을 말한다.원래의 삽입정렬본래의 삽입정렬은 키값과 키값 앞에 있는 값들을 간격 1로 비교하며 뒤로 넘기면서 정렬한다.shell sorting 셀정렬은 삽입정렬과 동일한 알고리즘이지만 gap

heap 정렬을 사용하기 위해서 heap을 먼저 구현함힙에 정렬할 요소를 다 넣고 오름차순으로 정렬하기 위해서 큰값부터 -1인덱스를 사용해서 삽입함 그리고 아까 실수한게 for 문에서 사용하는 인덱스로 습관적으로 i로 사용해서 계속 결과가 이상하게 나왔다.이 부분이 f

병합정렬 여러개의 문제를 작은 문제로 나누어서 해결하고 다시 큰문제로 합성하는것

quickSorting

tree의 순회방법과 탐색 알고리즘이진 탐색트리 삭제연산과 insert연산 중심으로 공부할 것이진탐색에서 주의해서 보아야 하는 것이노드가 양쪽의 자식을 가지고 있는 상황에서 이를 삭제하기위해서 삭제하려는 노드의 왼쪽자식의 오른쪽 끝 자손이나 오른쪽 자식에서 가장 왼쪽