git의 commit 데이터를 바탕으로, 각 커밋마다 어떤 변경점이 발생했는지 시각화하는 방안을 고민하다 이를 구현하고 있는 여러 라이브러리들을 참고하다 jsdiff 라이브러리 코드를 분석하게 되었습니다.
jsdiff 라이브러리 소개
jsdiff 라이브러리
A JavaScript text differencing implementation.
Based on the algorithm proposed in "An O(ND) Difference Algorithm and its Variations" (Myers, 1986).
jsdiff 라이브러리는 JavaScript로 작성된 텍스트 차이(diff) 비교 구현입니다. Myers 알고리즘을 기반으로 구현이 되어있습니다.
여기서 잠시 diff가 어떤 것인지 알아보겠습니다.
difference로부터 유래된 diff는 여기서 두 문자열의 차이를 계산하는 기능을 가지고 있습니다.
jsdiff의 기본적은 코드 구조는 아래와 같습니다.
src/
├── index.js
├── convert
├── patch
├── util
└── diff/
├── base.js
├── array.js
├── charactor.js
├── word.js
├── line.js
└── ...
diff: 차이점(diff) 관련 핵심 로직을 포함하는 디렉토리patch: 패치 관련 기능을 포함하는 디렉토리convert: 변환 관련 기능을 포함하는 디렉토리util: 유틸리티 함수들을 포함하는 디렉토리
jsdiff 라이브러리 코드 분석 (1)
눈여겨봐야 할 부분은 diff 디렉토리 내부의 base.js입니다.
base.js에서는 Diff를 prototype으로 구현하고 있으며,
이외의 array.js, charactor.js 등등은 Diff 프로토타입의 기능을 상속받되, 배열 처리에 필요한 메서드만 오버라이드를 통해 구현하고 있습니다.
Diff 프로토타입의 핵심적인 메서드로 diff()메서드가 있습니다.
diff(oldString, newString, options = {})프로토타입 내부에서 문자열 차이를 계산하는 실질적인 메서드로,
이전 문자열, 신규 문자열, 옵션을 props로 받고 있습니다.
let callback = options.callback;
if (typeof options === 'function') {
callback = options;
options = {};
}이 코드는 기본적으로 callback 변수에 options.callback의 값을 저장하고, options가 객체가 아닌 함수라면 바로 callback 변수에 options를 할당합니다.
이는 코드 사용의 확장성을 위한 것으로 diff 메서드를 사용할 때, options에 콜백을 그대로 전달하거나, option 객체와 콜백을 분리시켜 사용할 수 있게 하기 위해 위와 같은 구현이 들어갔습니다.
oldString = this.castInput(oldString, options);
newString = this.castInput(newString, options);
oldString = this.removeEmpty(this.tokenize(oldString, options));
newString = this.removeEmpty(this.tokenize(newString, options));이 코드는 타입을 변환하고(castInput), 문자열을 개별 토큰으로 분리하고(tokenize), 빈 값(토큰)을 제거합니다.
Diff 프로토타입 내부에서는 단순히 아래와 같이 메서드들이 구현되어 있지만,
castInput(value) {
return value;
},
tokenize(value) {
return Array.from(value);
},
join(chars) {
return chars.join('');
},이는 사용하는 곳에서 해당 메서드들을 오버라이드해서 사용하기 위해 확장성있게 만들어졌다고 볼 수 있습니다.
oldStirng, newString이 위에서 언급한 과정을 거치면 최종적으로 diff 계산에 적합한 형태로 데이터로 변환되고, 해당 값들을 기반으로 diff 알고리즘을 작동시키게 됩니다.
git diff 알고리즘
diff와 Git(diff)에서 주로 사용하는 비교 알고리즘은 Myers 알고리즘입니다.
git은 Myers 이외에도 Histogram 알고리즘 등을 사용하고 있는데,
두 알고리즘에 대해 간단하게 소개하려고 합니다.
Myers 알고리즘
Myers 알고리즘은 무려 1986년에 Eugene Myers에 의해 만들어진 알고리즘으로, 최소 편집 거리 기반으로 수학적으로 가장 짧은 최적의 diff를 구하는 알고리즘입니다.
LCS란 Longest Common Subsequence로, 직역하면 최장 공통 부분 수열이라는 의미입니다.
LCS에 대한 간단한 예시를 들어보겠습니다.
data1 = ABCBDAB
data2 = BDCABdata1과 data2에서 가능한 공통 부분 수열(연속될 필요는 없지만 순서는 반드시 유지되어야 함)은 AB, BCAB, BCB, BDAB, BCAB 등이 있습니다.
이 중 길이가 가장 긴 공통 부분 수열(LCS)은 길이가 4인 수열 중 하나인 BCAB 입니다.
이렇게 LCS를 찾는 방법은 데이터가 지금처럼 작을 때에는 무리없이 모든 경우를 나열해 찾을 수 있지만, 데이터가 복잡하고 길어질수록 구하기 어려워집니다.
이러한 문제를 해결하기 위해 보통 DP(동적 프로그래밍)을 활용해 LCS를 구합니다.
구하는 방법은 간단합니다.
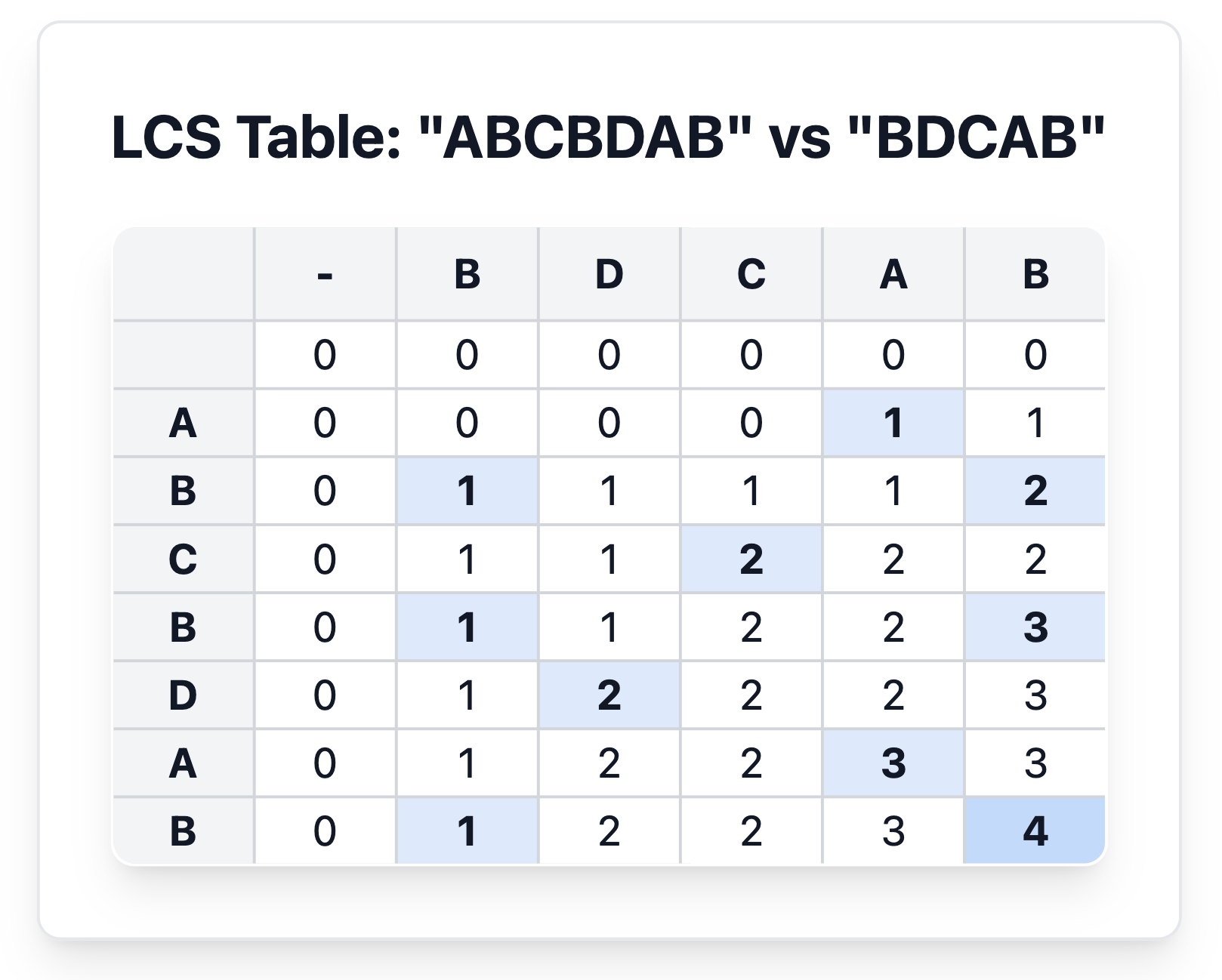
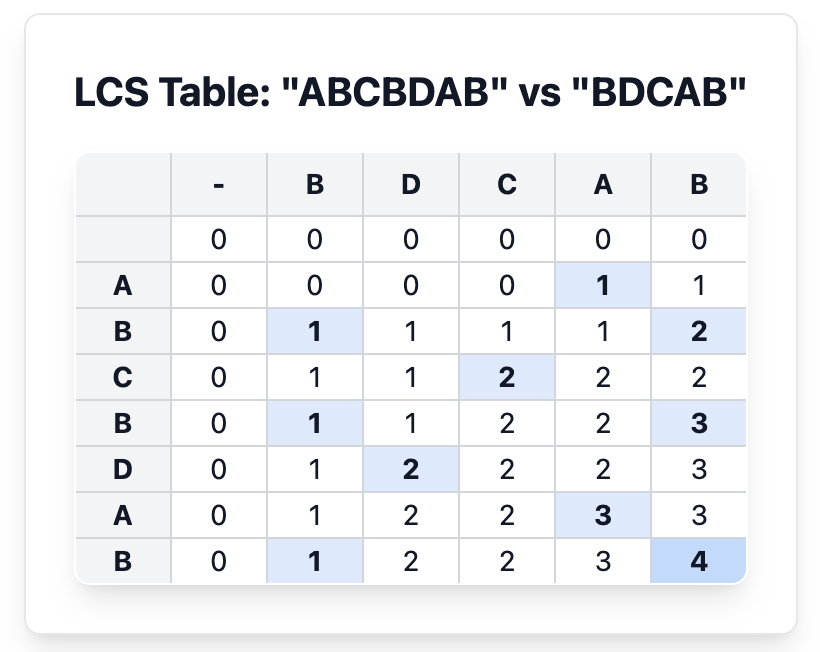
- DP 테이블을 두 문자열의 길이+1 만큼의 크기로 만들고 0으로 초기화 합니다.
- 비교할 때 두 문자가 같으면 1을 더하고, 두 문자가 다르면 이전에 계산된 값 중 더 큰 값을 가져옵니다.
- 테이블이 모두 채워지면 테이블의 마지막 셀부터 LCS 문자열을 추적합니다
- 추적은 문자가 같을 때, LCS에 추가하고 문자를 포함한 이전 상태(i-1, j-1)로 이동합니다. 문자가 일치하지 않으면 두 문자열 중 하나를 건너뜁니다.(LCS 길이가 더 길도록 dp[i-1][j]와 dp[i][j-1] 중 더 큰 값을 가진 셀로 이동))
따라서 dp[7][6](B) -> dp[6][5](A) -> dp[5][2](D) -> dp[4][3](B)을 거쳐 BADB가 나오고 이를 뒤집어 BDAB라는 LCS를 얻게 됩니다.
Histogram 알고리즘
histogram은 빈도 기반 분석을 통해 드물게 나타나는 라인들을 기준으로 삼아 나머지를 비교하는 방식으로, 인간이 읽기 쉬운 diff를 생성하는 특징을 가진 알고리즘입니다.
여기서 드물게 나타나는 라인은 말 그대로 비교할 두 파일에서 중복되지 않고 단 한 번만 등장하는 라인을 뜻합니다.
이러한 라인을 anchor로 삼아 해당 라인들을 기준으로 양쪽 텍스트를 나눠 각 부분에서 재귀적으로 비교를 수행합니다.
- 줄 빈도 계산
양쪽 버전의 모든 줄에 대해 등장 횟수를 계산합니다. 1회 등장 줄 = 앵커 후보

-
드문 줄 선택(Anchor)
1회만 등장한 줄 중 양쪽 모두에 있는 줄을 기준점(anchor)으로 선택합니다.

-
Anchor 기준으로 텍스트 분할
각 anchor를 기준으로 블록을 나누고, 나뉜 블록들끼리 재귀 비교합니다.

-
최종 결과
줄 수 최소화보다는 의미 단위로 잘린 diff를 만들어냅니다.
jsdiff 라이브러리 코드 분석 (2)
다시 본론으로 돌아와서, jsdiff 알고리즘은 difff를 조금 더 안정적인 Meyers 알고리즘을 사용해 구현했습니다.
(histogram 알고리즘은 순서나 맥락을 무시하고 자주 등장하는 항목에 초점을 맞추기 때문)
아래는 Meyers 알고리즘이 사용된 부분이 담긴 코드입니다.
let newLen = newString.length, oldLen = oldString.length;
let editLength = 1;
let maxEditLength = newLen + oldLen;
if(options.maxEditLength != null) {
maxEditLength = Math.min(maxEditLength, options.maxEditLength);
}
const maxExecutionTime = options.timeout ?? Infinity; // 최대 실행 시간 설정 (타임아웃)
const abortAfterTimestamp = Date.now() + maxExecutionTime; // 타임아웃 시간 계산
let bestPath = [{ oldPos: -1, lastComponent: undefined }];
let newPos = this.extractCommon(bestPath[0], newString, oldString, 0, options);
if (bestPath[0].oldPos + 1 >= oldLen && newPos + 1 >= newLen) {
return done(buildValues(self, bestPath[0].lastComponent, newString, oldString, self.useLongestToken));
}
let minDiagonalToConsider = -Infinity, maxDiagonalToConsider = Infinity;
function execEditLength() {
for (
let diagonalPath = Math.max(minDiagonalToConsider, -editLength);
diagonalPath <= Math.min(maxDiagonalToConsider, editLength);
diagonalPath += 2
) {
let basePath;
let removePath = bestPath[diagonalPath - 1],
addPath = bestPath[diagonalPath + 1];
if (removePath) {
bestPath[diagonalPath - 1] = undefined;
}
let canAdd = false;
if (addPath) {
const addPathNewPos = addPath.oldPos - diagonalPath;
canAdd = addPath && 0 <= addPathNewPos && addPathNewPos < newLen;
}
let canRemove = removePath && removePath.oldPos + 1 < oldLen;
if (!canAdd && !canRemove) {
bestPath[diagonalPath] = undefined;
continue;
}
if (!canRemove || (canAdd && removePath.oldPos < addPath.oldPos)) {
basePath = self.addToPath(addPath, true, false, 0, options);
} else {
basePath = self.addToPath(removePath, false, true, 1, options);
}
newPos = self.extractCommon(basePath, newString, oldString, diagonalPath, options);
if (basePath.oldPos + 1 >= oldLen && newPos + 1 >= newLen) {
return done(buildValues(self, basePath.lastComponent, newString, oldString, self.useLongestToken)) || true;
} else {
bestPath[diagonalPath] = basePath;
if (basePath.oldPos + 1 >= oldLen) {
maxDiagonalToConsider = Math.min(maxDiagonalToConsider, diagonalPath - 1);
}
if (newPos + 1 >= newLen) {
minDiagonalToConsider = Math.max(minDiagonalToConsider, diagonalPath + 1);
}
}
}
editLength++;
}
if (callback) {
(function exec() {
setTimeout(function() {
if (editLength > maxEditLength || Date.now() > abortAfterTimestamp) {
return callback();
}
if (!execEditLength()) {
exec();
}
}, 0);
}());
} else {
while (editLength <= maxEditLength && Date.now() <= abortAfterTimestamp) {
let ret = execEditLength();
if (ret) {
return ret;
}
}
}위에서부터 차근차근 분석해 보겠습니다.
최대 편집 가능 거리 구하기
편집 거리(Edit Distance)는 한 문자열을 다른 문자열로 변환하는 데 필요한 최소 연산 수 입니다.
let newLen = newString.length, oldLen = oldString.length;
let editLength = 1;
let maxEditLength = newLen + oldLen;
if(options.maxEditLength != null) {
maxEditLength = Math.min(maxEditLength, options.maxEditLength);
}비교할 두 문자열의 길이를 저장하고, 최악으로 나올 수 있는 편집 거리와 option을 통해 명시한 최대 편집 거리를 기반으로 최대 편집 가능 거리를 구합니다.
bestPath 초기화 및 최적화
let bestPath = [{ oldPos: -1, lastComponent: undefined }]; let newPos = this.extractCommon(bestPath[0], newString, oldString, 0, options);
if (bestPath[0].oldPos + 1 >= oldLen && newPos + 1 >= newLen) {
return done(buildValues(self, bestPath[0].lastComponent, newString, oldString, self.useLongestToken));
}우선 최단 경로를 저장할 bestPath를 초기화 시켜줍니다.
다음으로 extractCommon 메서드를 통해(이후에 설명 예정) 공통된 부분을 추출해 저장합니다.
이는 편집 거리에서 불필요한 연산을 줄이기 위해 미리 문자열의 시작부터 연속적으로 일치하는 부분을 찾아두는 과정입니다.
마지막으로 두 문자열이 일치하면 연산을 조기에 종료합니다.
코드만 보면 bestPath[0].oldPos + 1 >= oldLen가 -1 + 1 >= oldLen 과 일치할 것 같은데, 좋은 패턴은 아니지만 extractCommon 메서드에서 oldPos 값을 업데이트 해주고 있습니다.
execEditLength 함수 실행
if (callback) {
(function exec() {
setTimeout(function() {
if (editLength > maxEditLength || Date.now() > abortAfterTimestamp) {
return callback();
}
if (!execEditLength()) {
exec();
}
}, 0);
}());
} else {
while (editLength <= maxEditLength && Date.now() <= abortAfterTimestamp) {
let ret = execEditLength();
if (ret) {
return ret;
}
}
}jsdiff는 비동기 방식도 제공하기 때문에 callback 여부에 따라 반복하며 execEditLength를 실행합니다.
반복은 편집 거리가 최대 편집 거리보다 작거나 같을 때까지 진행됩니다.
execEditLength 함수 내부
let minDiagonalToConsider = -Infinity, maxDiagonalToConsider = Infinity;
function execEditLength() {
for (
let diagonalPath = Math.max(minDiagonalToConsider, -editLength); // 고려할 최소 대각선
diagonalPath <= Math.min(maxDiagonalToConsider, editLength); // 고려할 최대 대각선
diagonalPath += 2 // 홀/짝 대각선 간 이동 (2씩 증가)
) {
let basePath; // 현재 대각선의 기본 경로
let removePath = bestPath[diagonalPath - 1], // 삭제 연산을 위한 경로
addPath = bestPath[diagonalPath + 1]; // 추가 연산을 위한 경로
if (removePath) { // 메모리 효율화
bestPath[diagonalPath - 1] = undefined; // 더 이상 필요없는 경로 제거
}
let canAdd = false; // 추가 연산 가능 여부
if (addPath) { // 추가 경로가 존재하는 경우
const addPathNewPos = addPath.oldPos - diagonalPath; // 추가 후 새 위치 계산
canAdd = addPath && 0 <= addPathNewPos && addPathNewPos < newLen; // 유효한 위치인지 확인
}
let canRemove = removePath && removePath.oldPos + 1 < oldLen; // 삭제 연산 가능 여부
if (!canAdd && !canRemove) { // 어떤 연산도 불가능한 경우
bestPath[diagonalPath] = undefined; // 경로 가지치기
continue; // 다음 대각선으로 이동
}
// 최적 경로 선택 (추가 또는 삭제)
if (!canRemove || (canAdd && removePath.oldPos < addPath.oldPos)) { // 추가가 더 효율적인 경우
basePath = self.addToPath(addPath, true, false, 0, options); // 추가 연산 수행
} else { // 삭제가 더 효율적인 경우
basePath = self.addToPath(removePath, false, true, 1, options); // 삭제 연산 수행
}
// 공통 접미사 추출 (최적화)
newPos = self.extractCommon(basePath, newString, oldString, diagonalPath, options);
if (basePath.oldPos + 1 >= oldLen && newPos + 1 >= newLen) { // 두 문자열의 끝에 도달한 경우
return done(buildValues(self, basePath.lastComponent, newString, oldString, self.useLongestToken)) || true; // 결과 반환
} else { // 아직 끝에 도달하지 않은 경우
bestPath[diagonalPath] = basePath; // 현재 경로 저장
if (basePath.oldPos + 1 >= oldLen) { // 원본 문자열의 끝에 도달한 경우
maxDiagonalToConsider = Math.min(maxDiagonalToConsider, diagonalPath - 1); // 최대 대각선 제한
}
if (newPos + 1 >= newLen) { // 새 문자열의 끝에 도달한 경우
minDiagonalToConsider = Math.max(minDiagonalToConsider, diagonalPath + 1); // 최소 대각선 제한
}
}
}
editLength++; // 편집 거리 증가
}코드가 조금 복잡하게 느껴지는데, 하나씩 값을 대입해보면 어느정도 감을 잡을 수 있습니다.
diagonalPath는 Myers 차이 알고리즘에서 사용되는 개념으로, 두 문자열 간의 차이점을 찾는 방향을 나타냅니다.
x는 첫 번째 문자열, y는 두 번째 문자열을 뜻할 때,
diagonalPath(k) = x-y 의 값을 가집니다.
diagonalPath를 기반으로 만들어진 removePath와 addPath를 구한 후, 두 문자열의 끝에 모두 도달할때까지 추가/삭제/continue 과정을 진행합니다.
문자열 비교 예시
이를 쉽게 이해하기 위해 예시를 들어보겠습니다.
첫 번째(예전) 문자열이 'abc'이고, 두 번째(신규) 문자열이 'acb'라고 가정해 보겠습니다.
우선, (0,0)의 위치에서 앞서 있었던 bestPath 초기화 및 최적화 과정을 통해 앞에서부터 두 문자열이 일치하는 부분까지 진행합니다.
여기서는 [a]bc, [a]cb가 되겠네요.
execEditLength가 실행되고, diagonalPath는
Math.max(minDiagonalToConsider, -editLength) ~ Math.min(maxDiagonalToConsider, editLength. 즉, (-1 ~ 1)에 대해서 for문을 돌리게 됩니다.
step1. diagonalPath가 -1 ~ 1 일 때
execEditLength를 실행하기 전의 bestPath는 아래와 같았습니다.
[
{
oldPos: 0,
lastComponent: {
count: 1,
previousComponent: undefined,
added: false,
removed: false
}
}
]diagonalPath에 각각 -1, 1을 대입하면 bestPath는 아래와 같아집니다.(-1 index도 있기 때문에 객체로 표현함)
bestPath = {
"-1": {
oldPos: 1,
lastComponent: {
count: 1,
previousComponent: {
count: 1,
added: true,
removed: false,
previousComponent: {
count: 1,
added: false,
removed: false
}
},
added: false,
removed: false
}
},
"0": undefined,
"1": {
oldPos: 2,
lastComponent: {
count: 1,
previousComponent: {
count: 1,
added: false,
removed: true,
previousComponent: {
count: 1,
added: false,
removed: false
}
},
added: false,
removed: false
}
}
}두 문자열의 끝에 도달하지 않았기 때문에, for 문이 종료되고 editLength++가 실행됩니다.
step2. diagonalPath가 0 ~ 2 일 때
이전 과정 도중 minDiagonalToConsider 값이 0으로 변경되었기 때문에,
diagonalPath는 0부터 시작하게 됩니다.
diagonalPath가 0일 때,
removePath는 bestPath[-1], addPath는 bestPath[1]이 됩니다.
if (!canRemove || (canAdd && removePath.oldPos < addPath.oldPos)) 조건문에 의해 bestPath[-1].oldPos = 1, bestPath[1].oldPos = 2 가 되기 때문에 추가 연산을 실행합니다.
그 결과로 basePath는 아래와 같아집니다.
{
oldPos: 2,
lastComponent: {
count: 1,
added: true,
removed: false,
previousComponent: {
count: 1,
added: false,
removed: false,
previousComponent: {
count: 1,
added: false,
removed: true,
previousComponent: {
count: 1,
added: false,
removed: false
}
}
}
}
}해당 basePath는 if (basePath.oldPos + 1 >= oldLen && newPos + 1 >= newLen) 조건문에 만족하기 때문에 done(buildValues(...))이 실행되며 끝나게 됩니다.
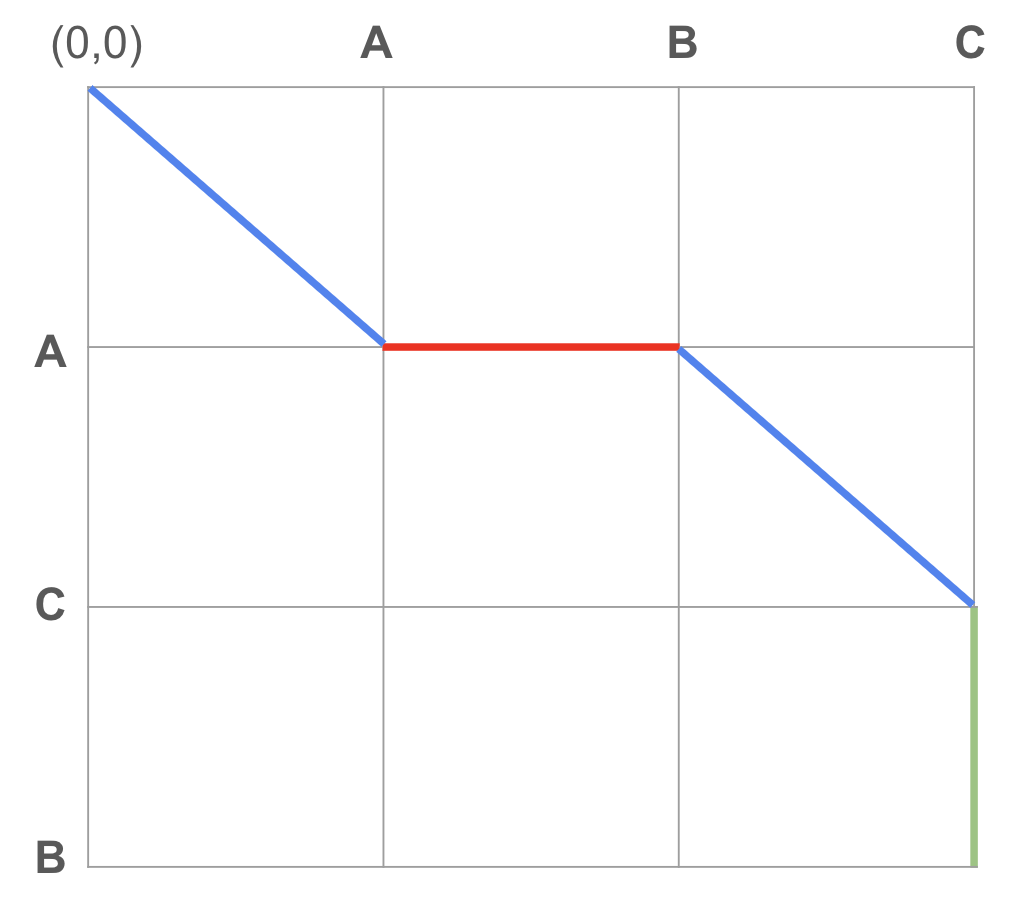
만들어진 basePath를 보면 중첩된 부분부터 거슬러 올라가면
1. continue
2. remove
3. continue
4. add
가 되는 것을 확인할 수 있습니다.
이미지에서 파란색 선은 continue, 빨간색 선은 remove, 초록색 선은 add를 나타냅니다.
buildValues 함수
function buildValues(diff, lastComponent, newString, oldString, useLongestToken) {
const components = [];
let nextComponent;
while (lastComponent) {
components.push(lastComponent);
nextComponent = lastComponent.previousComponent;
delete lastComponent.previousComponent;
lastComponent = nextComponent;
}
components.reverse();
let componentPos = 0,
componentLen = components.length,
newPos = 0,
oldPos = 0;
for (; componentPos < componentLen; componentPos++) {
let component = components[componentPos];
if (!component.removed) {
if (!component.added && useLongestToken) {
let value = newString.slice(newPos, newPos + component.count);
value = value.map(function(value, i) {
let oldValue = oldString[oldPos + i];
return oldValue.length > value.length ? oldValue : value;
});
component.value = diff.join(value);
} else {
component.value = diff.join(newString.slice(newPos, newPos + component.count));
}
newPos += component.count;
if (!component.added) {
oldPos += component.count;
}
} else {
component.value = diff.join(oldString.slice(oldPos, oldPos + component.count));
oldPos += component.count;
}
}
return components;
}bildValues 함수의 역할은 만들어진 basePath를 기반으로 실제 문자열에서 각 토큰의 변화 값을 기록해 배열에 저장합니다.
basePath의 lastComponent를 시작으로 점점 중첩된 previousComponent를 탐색해 components 배열에 추가합니다.
components 배열이 모두 만들어지면 이를 한 번 뒤집고, 배열을 순회하며 newString, oldString에 있던 실제 토큰을 가져와 value에 저장하게 됩니다.
모든 과정을 마치면 최종적으로 diff.diff('abc', 'acb')의 결과는 아래와 같게 나옵니다.
[
{ count: 1, added: false, removed: false, value: 'a' },
{ count: 1, added: false, removed: true, value: 'b' },
{ count: 1, added: false, removed: false, value: 'c' },
{ count: 1, added: true, removed: false, value: 'b' }
]마치며
소감
알고리즘을 이해하는 시간은 얼마 걸리지 않았지만, 이를 구현하는 코드를 이해하는데 생각보다 오랜 시간이 걸렸습니다.
특히 Myers 알고리즘을 이중 배열로 구현했겠구나 하고 생각했는데 연결 리스트로 중첩해서 구현이 되어있는 것을 보고 이해하는데 어느 정도의 시간이 소요되었던 것 같습니다.
하지만 직접 코드를 뜯어보며 알고리즘 구현에 대해 고민하고, 확장성과 최적화를 어떻게 구현했는지 보며 많은 것들을 얻어갈 수 있었습니다.
코드에 대해
전반적으로 코드는 최적화, 확장성 면에서 훌륭하게 구현되어 있었지만, 비교적 옛날 문법들이 많이 사용되었고, 코드의 가독성이 좋지는 않았던 부분은 아쉬웠습니다.
