수열
일정한 규칙에 따라 한 줄로 배열된 수의 열. a₁, a₂, a₃,…, aₙ의 꼴로 배열한 것으로, {aₙ}로 나타냄. 등차수열·등비수열·조화수열 등이 있다.
일반항
일반항이란 수열에서 n번째 항을 의미한다. 수열의 모든 항이 일반항을 만족하는 함수의 성격을 지닌다.
예를 들어
1,2,3,4,5.... 의 n번째 항은 n이다.
1,3,5,7,9.... 의 n번째 항은 2n-1 이다.
이처럼 수열의 규칙을 찾아 일반항을 구하는 것이 중요하다.
시그마
시그마는 ∑기호로 나타내며, 수열의 합을 나타내는 기호이다.
등차수열
연속된 두 항의 차이가 일정한 수열, 그 차이를 공차라고 한다.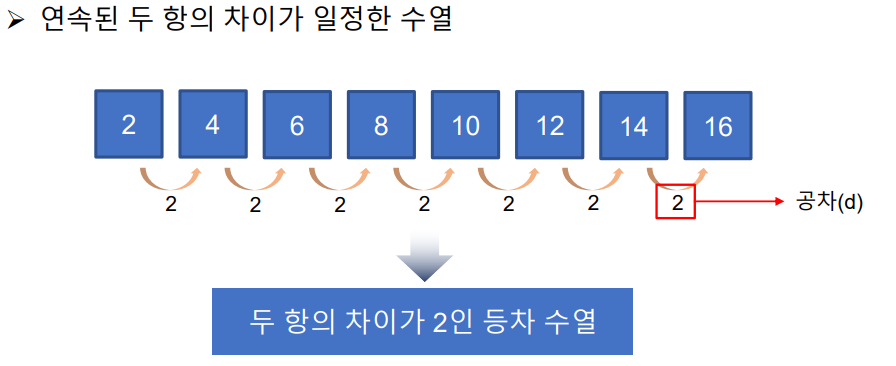
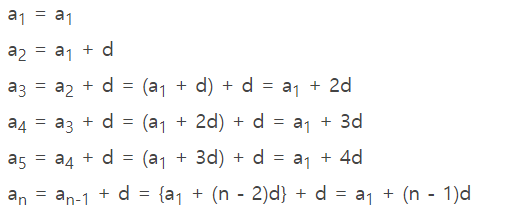
(Sn = n번째 항까지의 총합.)
등차수열 파이썬
등차 수열 나열하는 프로그램
a1 = int(input('첫 항 a1 입력 : '))
d = int(input('공차 d 입력 : '))
n = int(input('n 입력 : '))
sum = 0
for i in range(n):
print(f'{i+1}번째 항 : {a1+(i*d)}')
sum = sum + (a1+(i*d))
print(f'{n}번째 항까지의 합 : {sum}')
sn = int((n*((2*a1)+(n-1)*d))/2)
print(f'{n}번째 항까지의 합(공식) : {sn}') n번째 항 값 출력하는 프로그램
등차 수열 일반항 공식 = a1 + (n - 1) * d
a1 = int(input('첫 항 a1 입력 : '))
d = int(input('공차 d 입력 : '))
n = int(input('n 입력 : '))
nn = a1 + (n - 1) * d
print(f'{n}번째 항 : {nn}')n항 까지의 합을 나열하는 프로그램
a1 = int(input('첫 항 a1 입력 : '))
d = int(input('공차 d 입력 : '))
n = int(input('n 입력 : '))
sum = 0
for i in range(n):
sum = sum + (a1+(i*d))
print(f'{i+1}번째 항까지의 합 : {sum}')등비수열
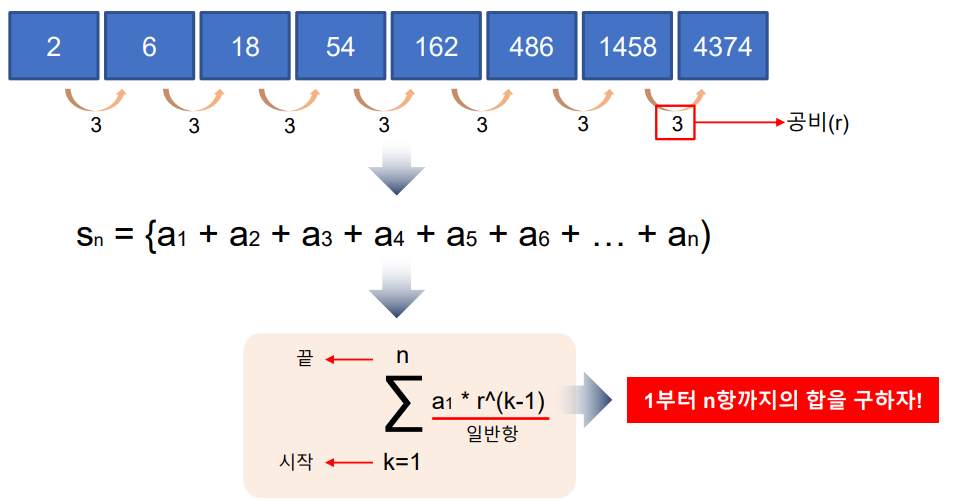
연속된 두 항의 비가 일정한 수열, 그 비를 공비라 한다.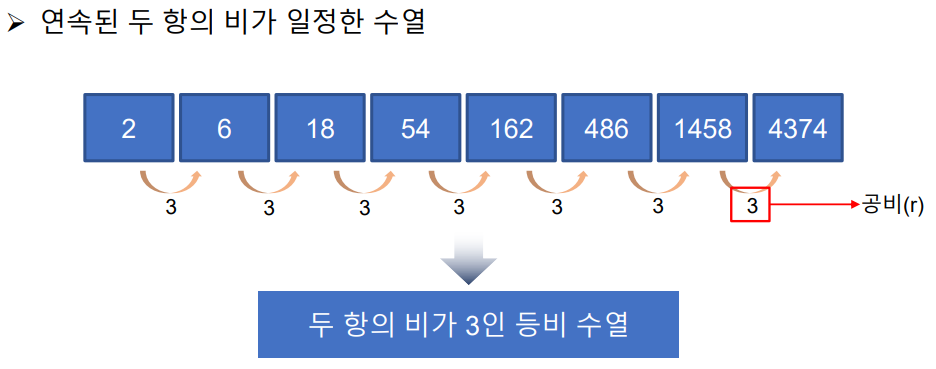
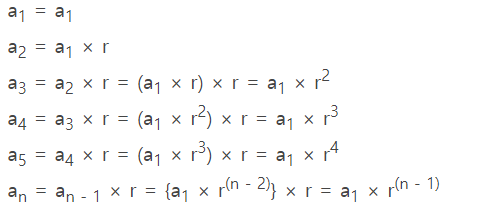
(Sn = n번째 항까지의 총합.)
등비수열 파이썬
등비 수열 나열하는 프로그램
a1 = int(input('첫 항 a1 입력 : '))
r = int(input('공비 r 입력 : '))
n = int(input('n 입력 : '))
sum = 0
for i in range(n):
print(f'{i+1}번째 항 : {a1*(r**(i))}')
sum = sum + (a1*(r**(i)))
print(f'{n}번째 항까지의 합 : {sum}')
sn = int(a1*((r**n)-1)/(r-1))
print(f'{n}번째 항까지의 합(공식) : {sn}') n번째 항 값 출력하는 프로그램
등비 수열 일반항 공식 = a1 * r^(n - 1)
a1 = int(input('첫 항 a1 입력 : '))
r = int(input('공비 r 입력 : '))
n = int(input('n 입력 : '))
nn = a1*(r**(n-1))
print(f'{n}번째 항 : {nn}')n항 까지의 합을 나열하는 프로그램
a1 = int(input('첫 항 a1 입력 : '))
r = int(input('공비 r 입력 : '))
n = int(input('n 입력 : '))
sum = 0
for i in range(n):
sum = sum + a1*(r**(i))
print(f'{i+1}번째 항까지의 합 : {sum}')