Topological sort

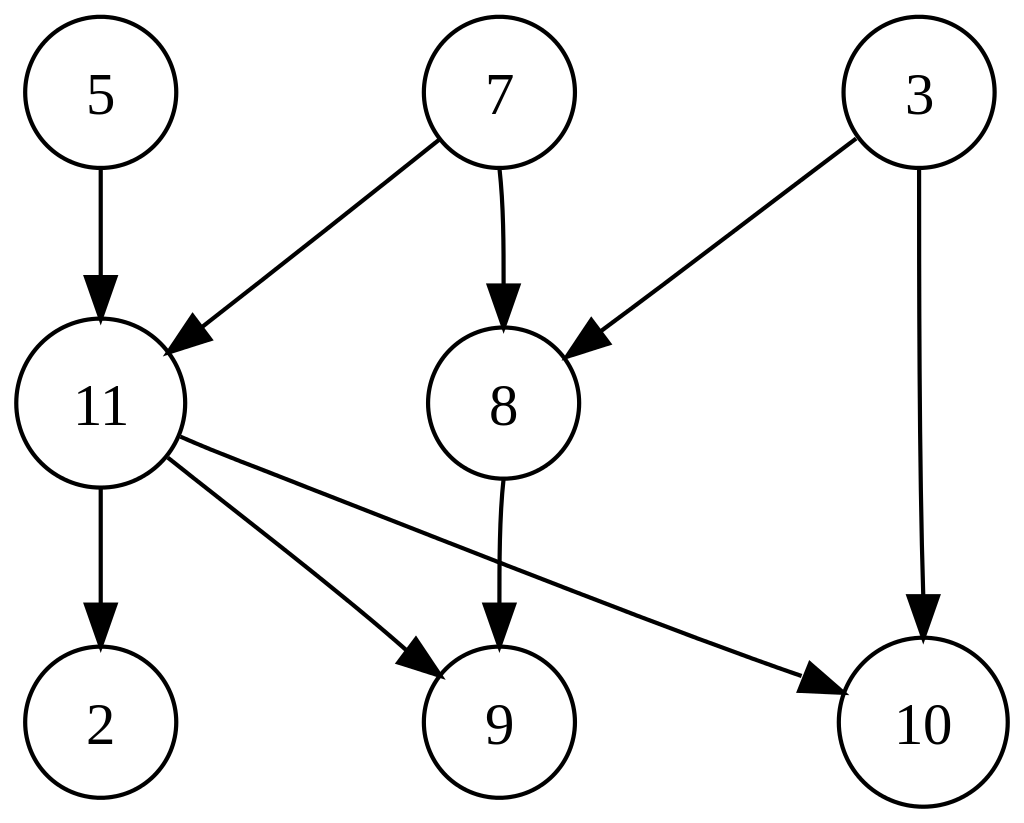
정의

참고: 위키백과
위상 정렬(topological sorting)은 directed graph(방향이 있는 그래프)의 노드(vertex)의 선행 순서를 거스르지 않으면서 나열하는 것을 의미한다.

topological sort를 가장 잘 설명해 줄 수 있는 예로 대학의 선수과목(prerequisite) 구조를 예로 들 수 있다. 만약 특정 수강과목에 선수과목이 있다면 그 선수 과목부터 수강해야 하므로, 특정 과목들을 수강해야 할 때 위상 정렬을 통해 올바른 수강 순서를 찾아낼 수 있다.

이와 같이 선후 관계가 정의된 그래프 구조 상에서 선후 관계에 따라 정렬하기 위해 위상 정렬을 이용할 수 있다.

정렬의 순서는 그래프의 구조에 따라 여러 개의 종류가 나올 수 있다. topological sort이 성립하기 위해서는 반드시 그래프의 순환이 존재하지 않아야 한다. 즉, 그래프가 DAG(directed acyclic graph)여야 한다.

수행과정

1. in-degree(들어오는 화살표)가 0인 노드를 찾는다.
2. 찾은 노드를 출력, 해당 노드와 그래프 삭제.
3. 남은 노드 중 in-degree가 0인 노드가 있으면 단계 1로 돌아가고, 아니면 알고리즘을 종료시킨다.

시간복잡도

인접 리스트를 사용할 경우: O(V+E)

예제 - 210. Course Schedule II

이걸 사용하면 leetcode의 207. Course Schedule, 210. Course Schedule II 문제를 아주 쉽게 풀 수 있다. 그 중 210번. Course Schedule II를 풀어본다.

문제 설명을 보면 pre[i] = [ai, bi] 의 의미는 bi 강의를 듣고 ai를 들을 수 있다고 나와있다. 방향 그래프로 표현하면 bi -> ai 이 되겠다.

prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.

class Solution {
public:
    vector<int> v[2000];
    
    vector<int> findOrder(int num, vector<vector<int>>& pre) {
        unordered_map<int, int> indegree;
        
        for (int i = 0; i < pre.size(); i++) {
            indegree[pre[i][0]]++;
            v[pre[i][1]].push_back(pre[i][0]);
        }
        
        queue<int> q;
        for (int i = 0; i < num; i++) {
            if (indegree[i] == 0) {
                q.push(i);
            }
        }
        
        vector<int> ans;
        while (!q.empty()) {
            int val = q.front();
            q.pop();
            ans.push_back(val);
            
            for (int i = 0; i < v[val].size(); i++) {
                indegree[v[val][i]]--;
                if (indegree[v[val][i]] == 0) {
                    q.push(v[val][i]);
                }
            }
        }
        
        if (ans.size() != num) {
            ans.clear();
        }
        return ans;
    }
};

소스 코드 설명

1. 노드와 각 노드들이 가르키는 다음 노드, 즉 방향이 저장된 인접 리스트 v를 만든다. vector 를 이용하여 만들었다.
2. 들어오는 방향의 그래프를 담는 indegree 맵을 만든다. unordered_map으로 한 이유는 굳이 정렬할 필요 없고, find 가 더 빠르기 때문이다.
   • unordered_map의 find(): O(N) in worst case
   • map의 find(): O(NlogN) in worst case

3. pre의 크기만큼 for문을 돌면서 in-degree(들어오는 방향)은 +1 을 해주고, 각 노드마다 연결된 다음 노드(강의)를 인접 리스트 v에 저장해준다.

4. in-degree(들어오는 방향)이 0인 노드들을 queue에 넣는다.
5. while 문을 돌면서 다음 노드의 in-degree를 -1한다. in-degree가 0인 노드의 다음 노드를 탐색하며 순서를 찾는다.

순환이 존재하는지 알수 있는 이유?
순환이 존재하면 in-degree가 0이 될 수 없어 전체 노드를 탐색할 수 없다.