Segment Tree

참고

VisualAlgo 사이트에서 시각적으로 확인할 수 있어서 좋았다.

설명

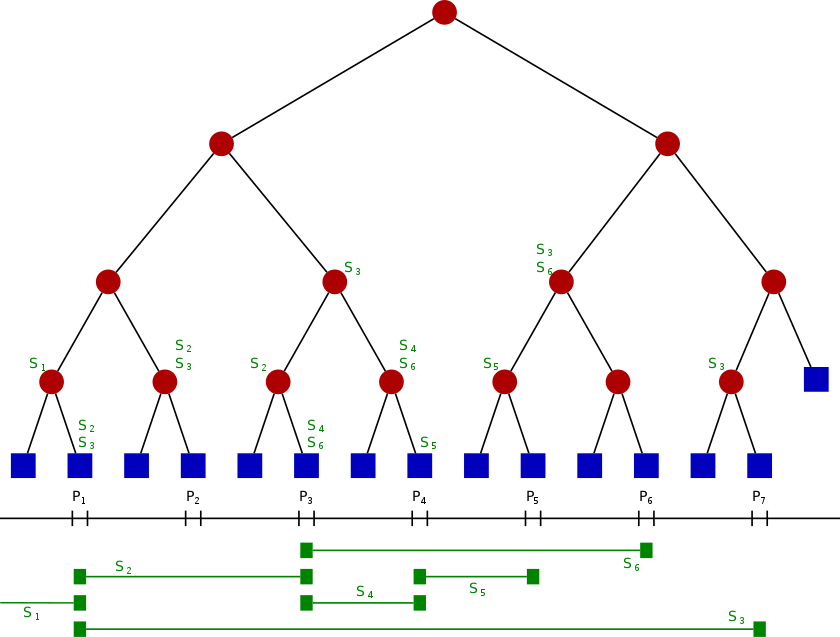
간격 또는 세그먼트에 대한 정보를 저장하는 데 사용되는 트리 데이터 구조입니다. 세그먼트 트리에 저장된 어떤 포인트를 찾을(query) 수 있다. 원칙적으로 정적 구조입니다. 즉, 일단 지어진 후에는 수정할 수없는 구조입니다.

A segment tree, also known as a statistic tree, is a tree data structure used for storing information about intervals, or segments. It allows querying which of the stored segments contain a given point. It is, in principle, a static structure; that is, it's a structure that cannot be modified once it's built. (출처: 위키백과)

세그먼트 트리는

• 바이너리 트리이다.
• 리프 노드: 배열의 그 수 자체
• 다른 노드: 왼쪽 자식과 오른쪽 자식의 union
  

문제 풀어보기 - 2158. Amount of New Area Painted Each Day

어떤 구간에 페인팅을 칠하는데, 한번 칠한곳은 다시 칠할 수 없다. 각 벡터마다 칠할 수 있는 구간을 구하는 문제이다.

해설

먼저, Segment Tree를 만든다.

class SegTree {
public:
    SegTree* left;
    SegTree* right;
    int start;
    int end;
    bool painted;

바이너리 트리이므로 left, right 를 가지고 있고, 구간인 start, end를 멤버 변수로 가지고 있다. 칠해졌는지 여부를 painted로 가지고 있다.

Segment tree의 root에는 입력 가능한 숫자인 0부터 50000을 interval 로 두고 시작한다.

root = new SegTree(0, 50000, false);

Update() 함수에서 세그먼트 트리와 찾고자하는 구간의 페인팅 여부를 파라미터로 준다.
헷갈릴수 있는데, Update() 함수를 돌면서 트리에서 필요한 구간을 만들면서 그 구간에서 페인팅 여부를 찾아 진행이 된다.

int Update(SegTree *tree, int start, int end) {
        if (tree->start == start && tree->end == end) {
            if (tree->painted == true) { // 이미 색깔이 칠해져있으면 멈춘다.
                return 0;
            }
            if (tree->left == NULL && tree->right == NULL) {
                tree->painted = true;
                return end-start;
            }
        }
        
        int mid = (tree->start + tree->end) / 2;

        if (tree->left == NULL) { // 필요하면 자식을 만든다. 왼쪽, 오른쪽 같이 만들기 때문에 왼쪽 하나만 비교했다.
        // 페인트의 마지막 숫자는 포함되지 않기때문에 오른쪽 노드 시작이 mid+1가 아니다.
            tree->left = new SegTree(tree->start, mid, tree->painted);
            tree->right = new SegTree(mid, tree->end, tree->painted);
        }
        
        int left = 0;
        int right = 0;
        if (start >= mid) {
            right = Update(tree->right, start, end);
        }
        else if (end <= mid) {
            left = Update(tree->left, start, end);
        }
        else {
            left = Update(tree->left, start, mid);
            right = Update(tree->right, mid, end);
        }
        tree->painted = tree->left->painted && tree->right->painted;
        return left+right;
        
    }

코드 전체

class SegTree {
public:
    SegTree* left;
    SegTree* right;
    int start;
    int end;
    bool painted;
    
    SegTree() {}
    SegTree(int sp, int ep, bool painted) {
        start = sp; 
        end = ep;
        left = right = NULL;
        this->painted = painted;
    }
};

class Solution {
public:
    SegTree *root;
    vector<int> amountPainted(vector<vector<int>>& paint) {
        root = new SegTree(0, 50000, false);
        vector<int> ans;
        
        for (int i = 0; i < paint.size(); i++) {
            ans.push_back(Update(root, paint[i][0], paint[i][1]));
        }
        return ans;
    }
    
    int Update(SegTree *tree, int start, int end) {
        if (tree->start == start && tree->end == end) {
            if (tree->painted == true) {
                return 0;
            }
            if (tree->left == NULL && tree->right == NULL) {
                tree->painted = true;
                return end-start;
            }
        }
        
        int mid = (tree->start + tree->end) / 2;

        if (tree->left == NULL) { // split the SegTree
            tree->left = new SegTree(tree->start, mid, tree->painted);
            tree->right = new SegTree(mid, tree->end, tree->painted);
        }
        
        int left = 0;
        int right = 0;
        if (start >= mid) {
            right = Update(tree->right, start, end);
        }
        else if (end <= mid) {
            left = Update(tree->left, start, end);
        }
        else {
            left = Update(tree->left, start, mid);
            right = Update(tree->right, mid, end);
        }
        tree->painted = tree->left->painted && tree->right->painted;
        return left+right;
        
    }
    
    
};