문제
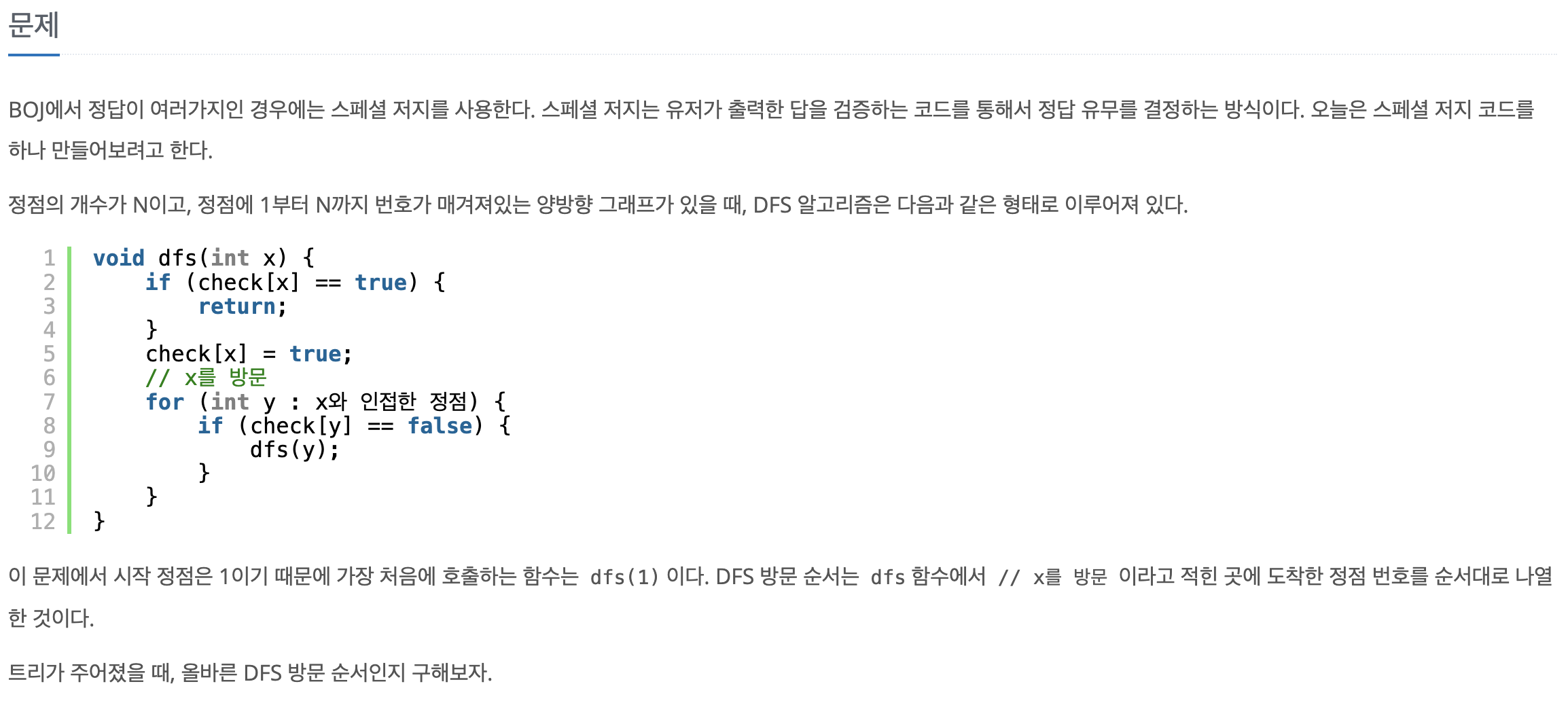
일단 주어진 DFS는 보편적인 형태이다. 트리의 출발점은 무조건 1로 고정되어 있다.
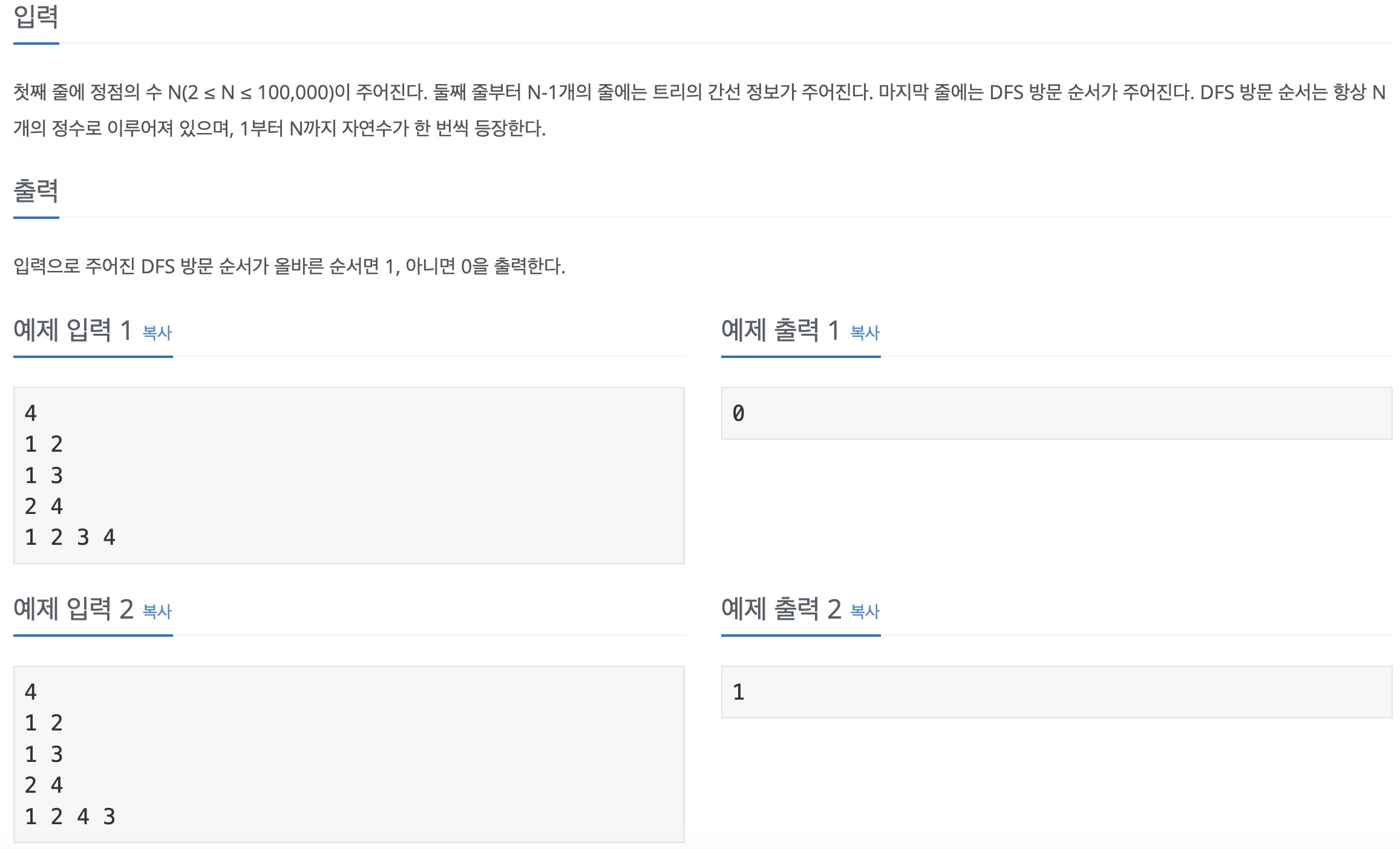
먼저 정점의 수를 입력받은 뒤, 여러 간선들을 입력받는다. 끝으로 DFS 이동 경로를 입력받아, 이 경로가 실제로 가능한 경로인지 판단하여 1이나 0을 출력하는 문제다.
시행착오 1
첫 번째로 접근했던 방식은, 탐색 경로를 만들어가며 노드들을 벡터에 넣고, 탐색한 노드가 총 N개임이 확인되면, 입력된 경로와 이 벡터가 동일한지 판단하는 방식이었다.

이 아이디어는 예제 3에서 무너진다.
1번 노드에서 갈 수 있는 노드는 2, 3, 4번이며, 단순 for문으로 경로를 만들어갈 경우 1-2-4-3이라는 경로만 확인할 수 있기에 오답이 된다.
즉 1-3-2-4가 가능한지 확인해야 하는데, 이 경우 1번 노드에서 2번, 3번, 4번 각각으로 출발하는 case를 모두 확인하며 입력된 경로가 가능한지 판단해야 하는데, 최대 노드가 10만개인데 이게 맞을까? 라는 의문이 들었다.
우리가 원하는 것은 가능한 전체 경로를 모조리 찾으면서 1-3-2-4가 존재하는지 확인하고 싶은 게 아니라, 그냥 1-3-2-4가 가능한지만 알고 싶다.
입력을 왜 줬을까? 우리는 그 입력이 실제로 가능한지만 빠르게 알고 싶다.
입력을 기반으로 우선순위를 부여한 다음 이를 그래프의 탐색 순서에 적용하는 것은 어떨까?
1번 노드가 2,3,4번 노드와 연결되어 있을 때, 1-3-2-4가 가능한지 알고 싶다면, 3번 노드의 우선순위를 가장 높게, 4번 노드의 우선순위를 가장 낮게 설정해주면 된다.
따라서 입력된 탐색 경로가 우선순위를 부여하는 기준점이 된다. 이를 order라는 배열을 통해 적용한다.


시행착오 2
그럼에도 불구하고 계속 틀렸습니다가 떠서 뭐가 문제인지 고민했으나, 굉장히 사소한 부분에서 오류를 찾았다. 트리는 무방향 그래프이기에, 당연히 양방향으로 간선을 입력해 주어야 하는데, 이를 생각하지 못한 것. 굉장히 부끄러운 일이다.

소스 코드
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
int n;
vector<int> v[100001];
vector<int> path, real;
int order[100001];
bool visited[100001];
bool cmp(int a, int b){
return order[a] < order[b];
} // 우선순위가 빠른 순으로 정렬
void DFS(int idx){
visited[idx] = true;
real.push_back(idx);
for(int i=0; i<v[idx].size(); i++){
if(!visited[v[idx][i]]){
DFS(v[idx][i]);
}
}
} // DFS
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n;
for(int i=0; i<n-1; i++){
int a, b;
cin >> a >> b;
v[a].push_back(b);
v[b].push_back(a);
} // 트리는 양방향 그래프이다..
for(int i=1; i<=n; i++){
int a;
cin >> a;
path.push_back(a); // 이동할 노드 입력
order[a] = i; // a의 우선순위는 i번쨰
}
for(int i=0; i<=n; i++){
sort(v[i].begin(), v[i].end(), cmp);
} // 입력에 따른 우선순위대로 정렬
DFS(1);
if(path == real) cout << 1 << '\n';
else cout << 0 << '\n';
return 0;
}교훈
- 입출력을 바로 보지 말고 문제를 잘 읽고 필요한 조건을 캐치했어야 했다.
- 트리는 무방향 그래프이다.