https://www.acmicpc.net/problem/15971

문제

두 로봇이 통신하기 위해 이동해야 하는 거리의 최솟값을 구해야 한다. 그래프 문제임을 빠르게 파악할 수 있다. (DFS, BFS 모두 가능하다)

그런데 조금 생각해야 할 게 있다. 이 문제는 단순하게 출발점에서 도착점까지의 거리를 구하는 문제가 아니라, 출발점과 도착점에 서 있는 두 로봇이 하나의 간선을 두고 마주볼 때 통신할 수 있으며, 이를 위해 이동하는 거리의 최솟값을 찾아야 한다.

입출력

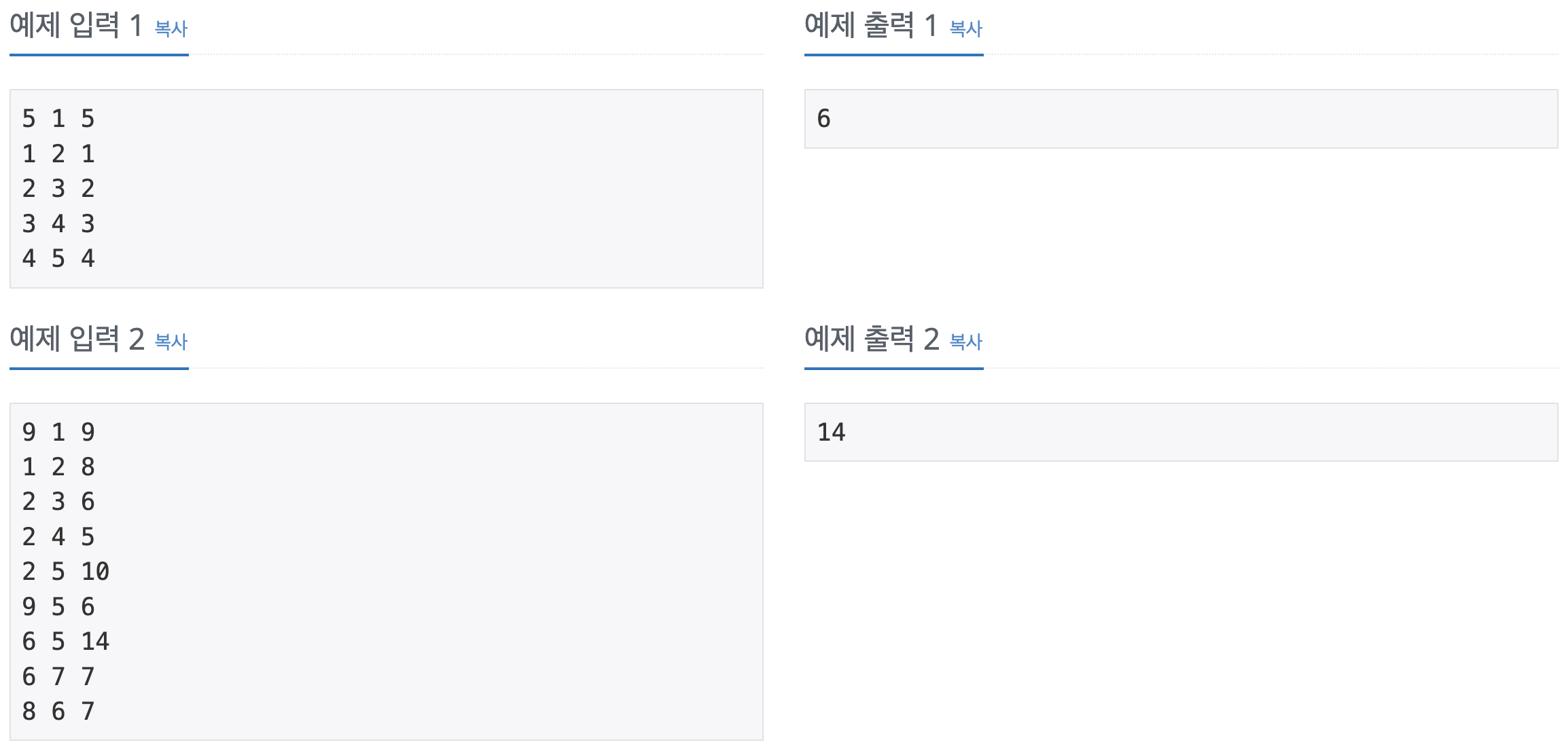예제 1에서, 출발점과 도착점 사이의 거리는 10이다. 출발 로봇이 4까지 이동하고 5에서 도착 로봇과 마주볼 때 최소임을 파악할 수 있다.

문제에서 설명한 예제 2에서는, 두 로봇이 2와 5에서 서로를 마주볼 때 최소가 된다.

예제 1과 2의 공통점은 마주보고 있는 간선이 전체 거리를 구성하는 간선 중 최댓값이라는 것이다.

즉 한 로봇에서 다른 한 로봇까지의 거리에서 가장 긴 간선을 빼면 된다. 이를 위해 DFS에서 경로 상의 간선들을 관리할 간선 리스트가 추가로 필요하다.

소스 코드

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
int n, s, e;
long sum = 0;
vector<pair<int, int> > v[100001];
vector<int> lines;
bool visited[100001];

void DFS(int pos, long sum){
    if(pos == e){ // 도착점에 도착함
        sort(lines.begin(), lines.end()); // 출발점~도착점까지의 거리에서 가장 긴 간선을 빼면 된다.
        if(lines.empty()) cout << sum << '\n'; // 출발/도착점이 동일한 경우에 대한 예외처리
        else cout << sum - lines.back() << '\n'; // 가장 긴 간선을 둔 양쪽 노드에서 만나면 최소이다.
        return;
    }

    if(visited[pos]) return;
    visited[pos] = true; // 방문처리
    for(int i=0; i<v[pos].size(); i++){
        if(!visited[v[pos][i].first]){
            lines.push_back(v[pos][i].second); // 간선 리스트에 추가
            DFS(v[pos][i].first, sum + v[pos][i].second);
            lines.pop_back(); // 재귀 빠져나오면 간선 리스트에서 배제
        }
    }
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n >> s >> e;
    for(int i=1; i<=n-1; i++){
        int a, b, c;
        cin >> a >> b >> c;

        v[a].push_back(make_pair(b, c));
        v[b].push_back(make_pair(a, c));
    } // 입력
    
    DFS(s, 0);
    return 0;
}

교훈

• 그래프에서 최솟값 등의 optimal을 요구하는 문제라면 어떻게 optimal한 상황을 도출할 수 있을지 고민하는 시간을 가져보자.
• 최단 거리라고 해서 기계적으로 BFS를 꺼내기보다는, 상황에 맞게 유연한 판단이 필요하다.