10723번 판게아 1

문제

조금 독특한 요구사항이 있었던 MST 문제였다.
문제에서 추출할 수 있는 정보는 다음과 같다.

• 매번 도로가 추가될 때마다 모든 도시가 서로 직간접적으로 연결
• 선택된 도로들의 길이의 합이 최소여야 함(최소 스패닝 트리)

도로가 추가될 때마다 MST를 새로 형성해야 한다는 것만 캐치하면 해결할 수 있다.
Kruskal 알고리즘으로 문제를 해결하였다.

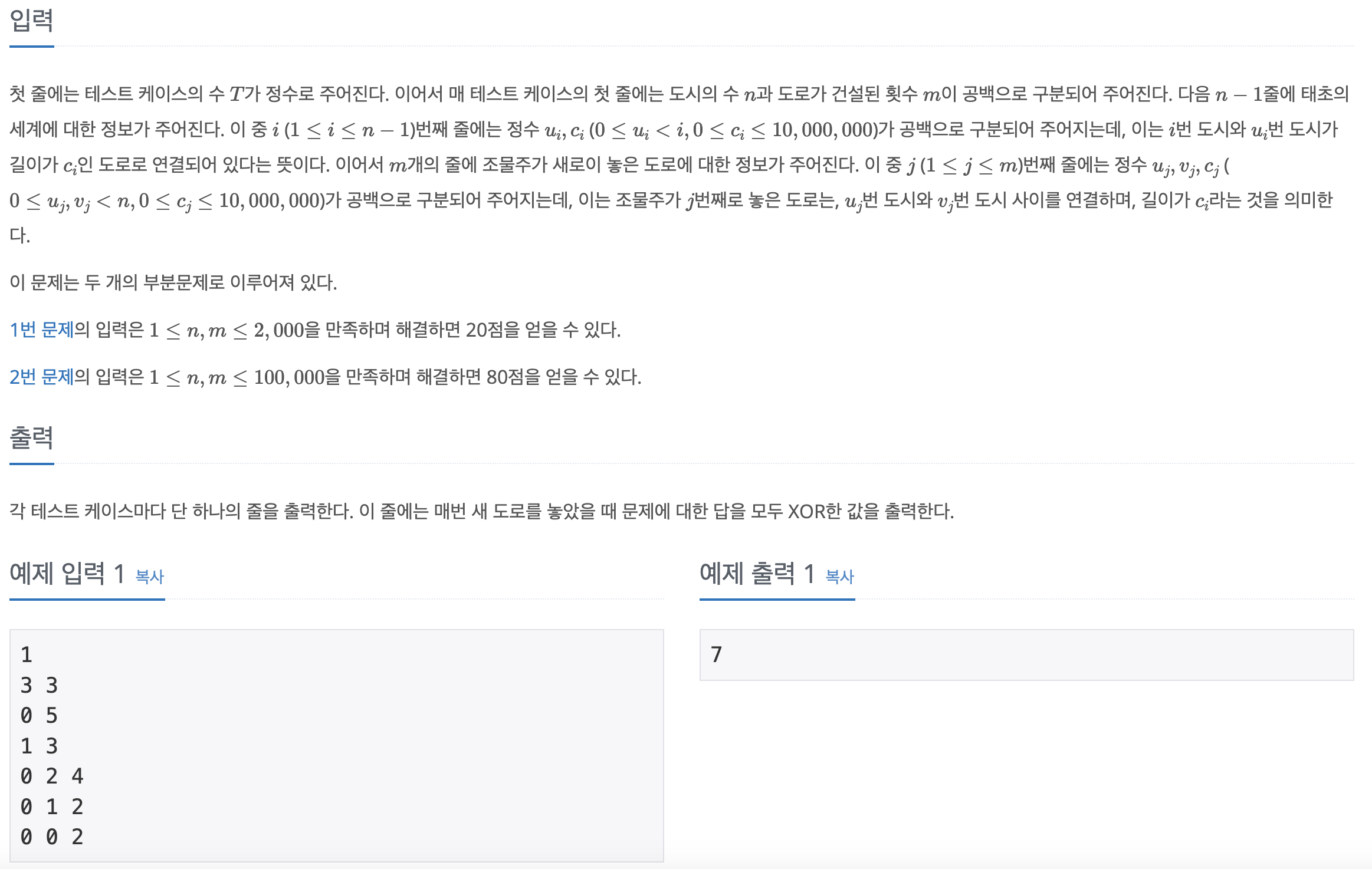
테스트케이스 t, n과 m을 입력받은 뒤,
1 ~ n-1까지는 기존의 도로를 입력
1 ~ m 까지는 조물주가 새로 추가한 도로를 입력하며, 이때 입력 직후 MST를 형성하는 것을 반복하며 각 도로 연결 시 MST 형성 비용을 모두 XOR 연산해준다.

참고로 A XOR B는 A ^= B로 표현된다.

소스 코드

// kruskal 알고리즘 활용
#include <iostream>
#include <algorithm>

using namespace std;
int t, n, m;
long long res = 0; // 각 도로 추가 시 형성되는 MST의 비용
long long total = 0; // 출력할 결과
int parent[100001];
vector<pair<long long, pair<int, int> > > v; // 비용, 출발점, 도착점

int find(int num){
    if(num == parent[num])
        return num;
    return parent[num] = find(parent[num]);
}

void merge(int a, int b){
    a = find(a);
    b = find(b);
    parent[a] = b;
} // 유니온 파인드

void build(){
    sort(v.begin(), v.end()); // 정렬 및 MST 형성
    for(int i=0; i<v.size(); i++){
        int s = v[i].second.first;
        int e = v[i].second.second;
        long long val = v[i].first;

        if(find(s) != find(e)){
            merge(s, e);
            res += val;
        }
    }
    total ^= res; // XOR 연산
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> t;
    for(int a=0; a<t; a++){
        v.clear();
        total = 0; // 테케마다 초기화
        
        cin >> n >> m;
        for(int i=1; i<=n-1; i++){
            int a;
            long long b;
            cin >> a >> b;
            v.push_back(make_pair(b, make_pair(i, a)));
        } // 기존 도로

        for(int i=1; i<=m; i++){
            for(int j=0; j<=n; j++){
                parent[j] = j;
            }
            res = 0;
             // 한 줄씩 추가될때마다 아예 새로 MST를 구축하는 비용들을 새로 계산해야 하므로,
             // parent와 res의 초기화가 요구된다.

            int a, b;
            long long c;
            cin >> a >> b >> c;
            v.push_back(make_pair(c, make_pair(a, b)));
            build(); // 도로 추가 직후 MST 형성
        }
        cout << total << '\n'; // 테케별 최종 결과 출력
    }
    return 0;
}

교훈

• MST는 형성하는 알고리즘인 kruskal 및 prim 모두 알아두어야 한다.
• 가중치 입력 시 long long 자료형이 필요한 상황인지 항상 파악하는 습관을 들이자.
• A XOR B = A ^= B이다.