[자료구조] 이진탐색트리(Binary Search Tree)

이진탐색트리

모든 노드의 왼쪽 서브 트리는 해당 노드의 값보다 작은 값들을 가지고, 모든 노드의 오른쪽 서브 트리는 해당 노드의 값보다 큰 값만 가진다.
=> 이진 탐색 트리의 최대값은 트리의 가장 오른쪽에, 최소값은 트리의 가장 왼쪽에 위치한다.

---

이진 탐색 트리의 순회 방법

순회는 트리에 있는 모든 노드들을 방문하는 것을 말한다.

In-order traversal(중위 순회)

1. 재귀적으로 왼쪽 서브 트리를 순회한다.
2. 현재 노드를 방문한다.
3. 재귀적으로 오른쪽 서브 트리를 순회한다.
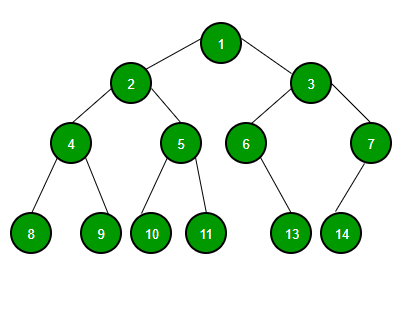
   위의 트리를 중위 순회한다면 노드들을 다음과 같이 방문하게 된다:

• 8 - 4 - 9 - 2 - 10 - 5 - 11 - 1 - 6 - 13 - 3 - 14 - 7

Pre-order traversal(전위 순회)

1. 현재 노드를 방문한다.
2. 재귀적으로 왼쪽 서브트리를 순회한다
3. 재귀적으로 오른쪽 서브 트리를 순회한다.
   위의 트리를 전위 순회한다면 노드들을 다음과 같이 방문하게 된다:

• 1 - 2 - 4 - 8 - 9 - 5 - 10 - 11 - 3 - 6 - 13 - 7 - 14

Post-order traversal(후위 순회)

1. 재귀적으로 왼쪽 서브 트리를 순회한다.
2. 재귀적으로 오른쪽 서브 트리를 순회한다.
3. 현재 노드를 방문한다.
   위의 트리를 후위 순회한다면 노드들을 다음과 같이 방문하게 된다:

• 8 - 9 - 4 - 10 - 11 - 5 - 2 - 13 - 6 - 14 - 7 - 3 - 1

---

이진 탐색 트리의 장단점

장점

• 삽입, 삭제가 유연하다. 삭제된 노드를 가르키고 있던 reference만 조정 해주면 된다.
• 값의 크기에 따라 좌/우 서브트리가 나눠지기 때문에 삽입 / 삭제 / 검색이 일반적으로 빠르다 O(logN).
• 값의 순서대로 순회가 가능하다.

단점

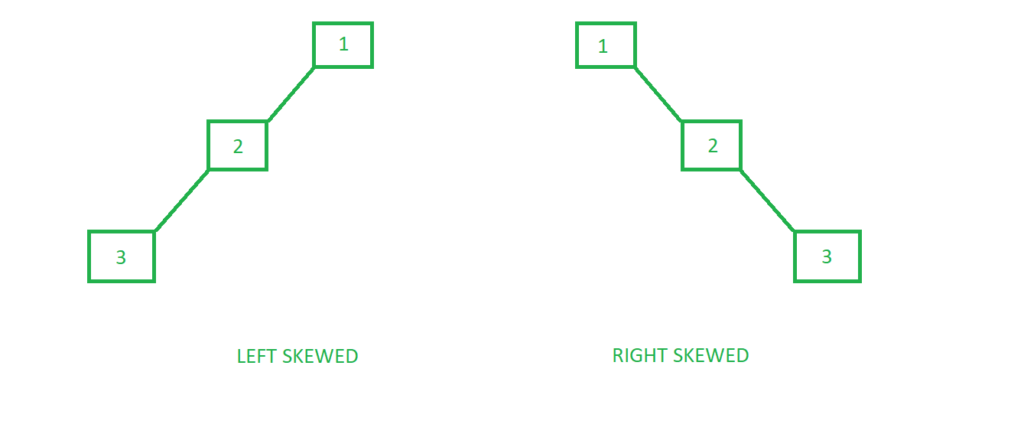
최악의 경우 삽입 / 삭제 / 검색이 Θ(N) (편향된 트리, 그냥 리스트가 되어버린다.)
이 문제를 해결하기 위해 스스로 균형을 잡는 이진 탐색 트리가 사용된다.
ex) AVL 트리, Red-Black 트리

이미지 출처 : geeksforgeeks