[백준] 15686번: 치킨 배달

https://www.acmicpc.net/problem/15686

initial (very inefficient, dfs backtracking is faster)

Here I used combinations to find out total possible outcomes of selecting m chicken places. Then I would be calculating the minimum distance from chicken place to house but this is wrong! Now that I think about it it is obvious why it is wrong but let’s look at this image where I did min distance from chicken to house

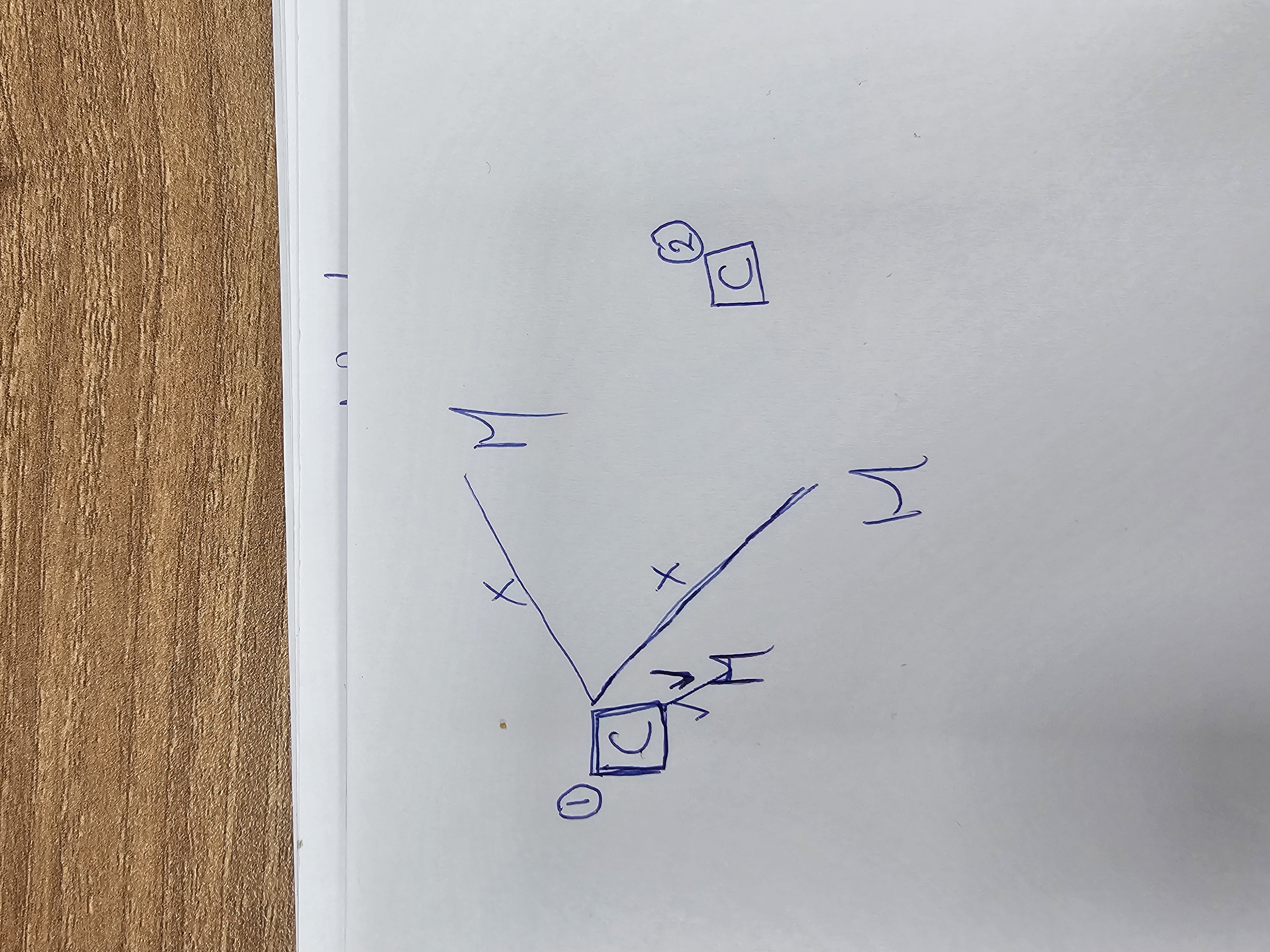
We should be calculating min distance from house to chicken, not chicken to house because for each house, we need to calculate the min distance to chicken and add all the min distance together. But if we do the other way around, other houses, which might be far from chicken house, may not be considered cuz of min() so effectively we are leaving out some houses behind if we do it like this.

you can code like

correct
for comb in combi:
    hola = 0
    for h in tmp1:
        kirk = 999
        for c in comb:
        
wrong
for comb in combi:
    hola = 0
    for c in comb:
        kirk = 999
        for h in tmp1:

So plan well on paper! I was so sleepy i didnt plan and just coded right away.

solution (ineff)

from itertools import combinations
import sys
input = sys.stdin.readline

n, m = map(int, input().split())
graph = []
tmp = []
tmp1 = []

for _ in range(n):
    graph.append(list(map(int, input().split())))

for i in range(len(graph)):
    for j in range(len(graph[0])):
        if graph[i][j] == 2:
            tmp.append((i, j))
        if graph[i][j] == 1:
            tmp1.append((i, j))

combi = combinations(tmp, m)

ans = int(1e9)

for comb in combi:
    hola = 0
    for h in tmp1:
        kirk = 999
        for c in comb:
            kirk = min(kirk, abs(c[0] - h[0]) + abs(c[1] - h[1]))
        hola += kirk
    ans = min(hola, ans)

print(ans)

dfs bbacktracking way (much more eff.)

Instead of computing all possible combinations beforehand, why not we use backtracking that traverses all pairs and the end recursion condition is when depth reaches m? This would be more eff!

but the actual distance calculation is done here

for r in range(N):
    for c in range(N):
        if city[r][c] == 1:
            houses.append((r, c))
            chicken_dists.append([])
        elif city[r][c] == 2:
            chickens.append((r, c))
            visited.append(False)

for h_i, (h_r, h_c) in enumerate(houses):
    for c_i, (c_r, c_c) in enumerate(chickens):
        chicken_dists[h_i].append((abs(h_r - c_r) + abs(h_c - c_c), c_i))
        chicken_dists[h_i].sort()

so solution but Im not sure why we have to sort chicken distance each time the distance is calculated. I thought it is just for optimisation but if it is commented out it is wrong (tbc)

import sys
input = sys.stdin.readline

def dfs(depth, now):
    global ans

    if depth == M:
        cnt = 0
        for dist_info in chicken_dists:
            for dist, idx in dist_info:
                if visited[idx]:
                    cnt += dist
                    break
        ans = min(ans, cnt)
        return

    for i in range(now, len(chickens)):
        if not visited[i]:
            visited[i] = True
            dfs(depth + 1, i + 1)
            visited[i] = False

N, M = map(int, input().split())
city = [list(map(int, input().split())) for _ in range(N)]

houses = []
chickens = []
chicken_dists = []
visited = []

for r in range(N):
    for c in range(N):
        if city[r][c] == 1:
            houses.append((r, c))
            chicken_dists.append([])
        elif city[r][c] == 2:
            chickens.append((r, c))
            visited.append(False)

for h_i, (h_r, h_c) in enumerate(houses):
    for c_i, (c_r, c_c) in enumerate(chickens):
        chicken_dists[h_i].append((abs(h_r - c_r) + abs(h_c - c_c), c_i))
        chicken_dists[h_i].sort()

ans = 987654321

dfs(0, 0)
print(ans)

complexity

So reading input takes nn time,
Combination is nm choose m
That double for loop is n^2 but since we are iterating for each combination it is nm choose m n^2

1. Parsing the input grid and creating lists tmp and tmp1 takes O(n*m) time, where n and m are the dimensions of the grid.

2. Generating combinations using itertools.combinations takes O((nm choose m)) time. This is because you are generating all possible combinations of m cells out of nm total cells.

3. Calculating the minimum distance for each combination involves iterating over m cells in the combination and for each cell, calculating the distance to each of the m cells in tmp1. This part takes O(m^2) time for each combination. Since you have O((nm choose m)) combinations, the total time complexity for this part is O((nm choose m) * m^2).

4. Finding the overall minimum distance by iterating through the combinations takes O((n*m choose m)) time. In practice, this step involves comparing m^2 values for each combination.

So, the overall time complexity of your code is approximately O((nm choose m) m^2). The time complexity depends on the number of combinations and the work done for each combination.

I hope this clarifies the time complexity of your code.