[백준] 1504번: 특정한 최단 경로

https://www.acmicpc.net/problem/1504

initial

I got the solution right but my code is 4x inefficient idk why

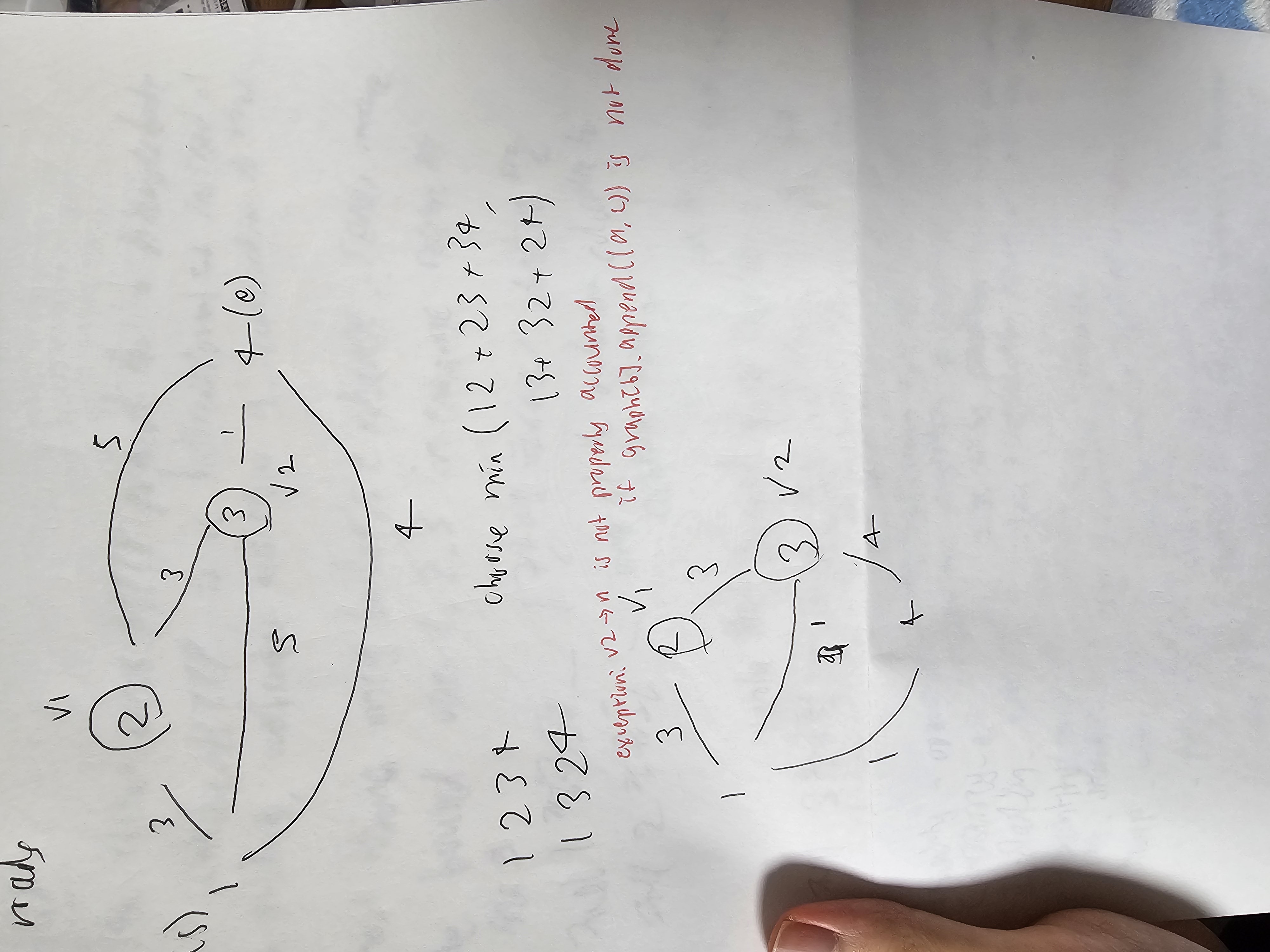
So the minimum cost while having need to pass these 2 cities (v1,v2) , can be expressed as 1234 or 1324. From city 1, you can either go to v1 or v2 so you take the minimum cost of these 2 paths.

One mistake I made is that I didnt append bidirectionally for my graph so for test case like

4 5
1 2 3
1 3 1
1 4 1
2 3 3
3 4 4
2 3

where you can see it inmy pic, v2 to n is not properly calculated bcos graph is not bidirectionally marked. So take care.

another thing is rmb if you add like a list to a parameter, you are storing the reference, not the actual object. TO store the object, not the reference, you have to use .copy() or else for my case where dijkstra is performed 3 times, if you keep passing tmp as list parameter, the same tmp 1 object will be used on and on, which gives wrong answer.

VERY IMPORTANT

to make it more efficient for dijkstra, we should not traverse when the current cost is higher than the recorded cost to travel to this particualar node (i.e. if cur_cost>distance[cur_node]) then it is not work traversing it cuz the cost is high.

This improves around 2.5times from 1200ms to 500ms. Good!

solution mine (after adding that important eff code)

1200ms ineff ->500ms

import heapq
import math
from collections import defaultdict, deque
import sys
input = sys.stdin.readline

n,m=map(int,input().split())
graph=defaultdict(list)
for _ in range(m):
    a,b,c = map(int,input().split())
    graph[a].append((b,c))
    graph[b].append((a,c))
v1,v2=map(int,input().split())
heap=[]
heapq.heapify(heap)
tmp = [int(10e18) for _ in range(n+1)]
def dijkstra(node,distance):
    distance[node]=0
    heapq.heappush(heap,(0,node))
    while heap:
        cur_cost,cur_node = heapq.heappop(heap)
        ## IMPORTANTTTTTTTTTTTTTTT ###############
        if cur_cost>distance[cur_node]:
            continue
        for hola in graph[cur_node]:
            next_node,next_cost = hola
            if cur_cost+next_cost <distance[next_node]:
                distance[next_node]=cur_cost+next_cost
                heapq.heappush(heap,((cur_cost+next_cost,next_node)))
    return distance
distance1=dijkstra(1,tmp.copy())
distance2=dijkstra(v1,tmp.copy())
distance3=dijkstra(v2,tmp.copy())
min1 = distance1[v1]+distance2[v2]+distance3[n]
min2 = distance1[v2]+distance3[v1]+distance2[n]
if min(min1,min2)>=int(10e18):
    print(-1)
else:
    print(min(min1,min2))

OMPLEXITY

WAS DIJKSTRA log n? forgot

firstly heapq takes log v time and since edge is processed once, it is v+e log v.

The time complexity of your modified solution is still O((V + E) log V), where V is the number of vertices and E is the number of edges in the graph. This is because each edge is processed once, and the priority queue operations (heap pop and push) take O(log V) time.

The space complexity is O(V + E), where V is the number of vertices and E is the number of edges. This is due to the storage of the graph in the graph dictionary and the distance arrays.

In your modified solution:

• The graph defaultdict stores the edges in adjacency list format, and its space complexity is O(V + E).
• The heap priority queue is used to store nodes and their tentative distances during Dijkstra's algorithm. The space complexity is O(V).
• The tmp list is used to initialize the distances, and its space complexity is O(V).

Therefore, the overall space complexity is O(V + E).

The implementation looks correct and should provide the correct output for the problem.