[프로그래머스] 모음 사전 - JS

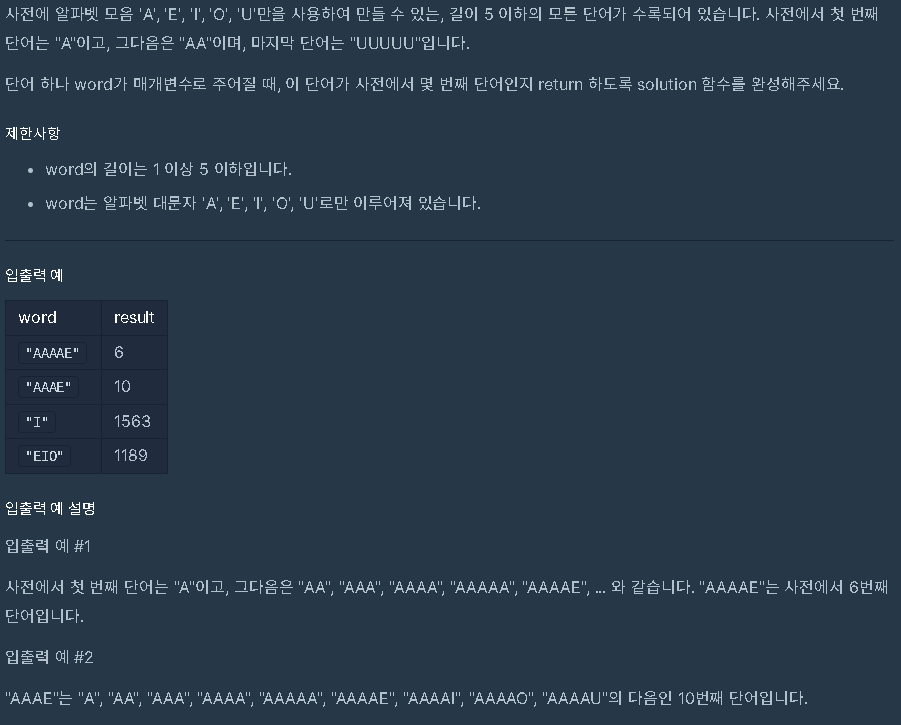
문제

풀이

AAAA = 4+0 = 4
AAAE = 4+6 = 10
AAAI = 4+6+6 = 10
둘째 자릿수가 바뀌는데 필요한 수는 6인 것을 알 수 있다.
AAA에서 AAE로 가는 경우를 생각해보자.
1. AAAA에서 AAE까지는 총 6*5 = 30의 경우의 수이다.
2. 그렇다면 AAA에서 AAAA로 가는 1만을 더해주면 된다.
이 규칙을 배열로 만들면

const plus = [?, ?, ?, 1*5+1, 1];
const plus = [?, ?, 6*5+1, 6, 1];
const plus = [?, 31*5+1, 31, 6, 1];
const plus = [156*5+1, 156, 31, 6, 1];
const plus = [781, 156, 31, 6, 1];

이 된다.

function solution(word) {
  let answer = 0;
  let arr = ["A", "E", "I", "O", "U"];
  const plus = [781, 156, 31, 6, 1];

  for (let i = 0; i < word.length; i++) {
    answer += plus[i] * arr.indexOf(word[i]) + 1;
  }
  return answer;
}