[프로그래머스] k진수에서 소수 개수 구하기(Python)

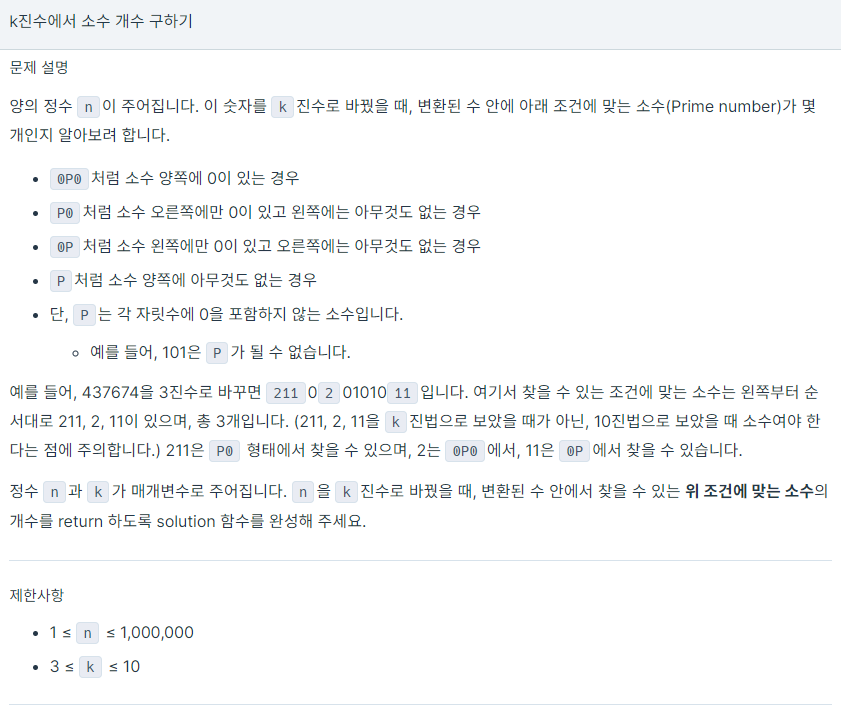
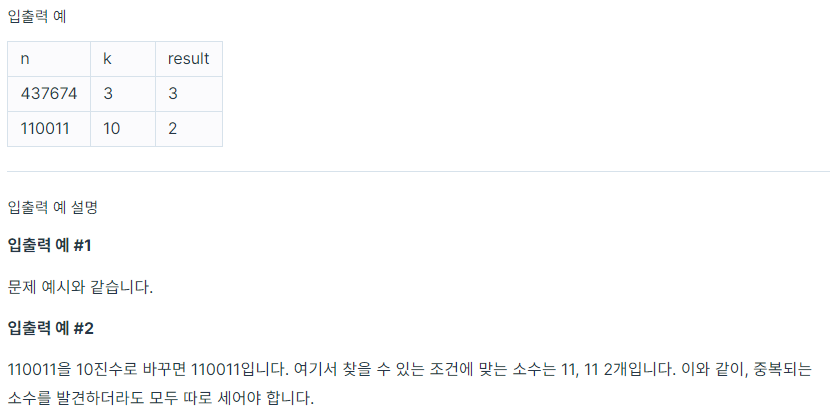
💻 문제 - Lv.2

2022 KAKAO BLIND RECRUITMENT

📝 소수 판별

x의 소수 판별 알고리즘

1. 2부터 (x-1)까지 모든 수(i)를 확인하며 x가 i에 나누어떨어진다면 소수가 아니고 그렇지 않다면 소수이다.

   2부터 (x-1)까지 확인한다는 점에서 시간 복잡도는 O(x)이다.

2. 소수가 아닌 경우는 약수를 가진다.

   모든 약수는 곱셈 연산에 대해 대칭을 이룬다. 예를 들어, 16의 약수는 1, 2, 4, 8, 16으로 4를 기준으로 대칭이다.

   즉, 약수를 찾을 때 가운데 약수(x의 제곱근)까지 확인해도 된다. 예를 들어, 2로 나누어 떨어지면 8로도 나누어 떨어진다.

   이때, 시간 복잡도는 O(x**1/2)이다.

👉 제출 코드

문제 조건에 맞게 다음과 같은 순서로 구현한다.

1. 진수 변환
   divmod 함수를 이용하여 k진수로 변환한다.
2. 0을 기준으로 쪼개기
   split 함수를 사용하기 위해 join 함수를 사용하여 배열을 문자열로 바꾸고 여백을 없앤 후 쪼갠다.
3. 소수 판별
   math 라이브러리를 사용하여 is_prime_number함수를 구현한다. 0이 연속된 경우 result에 빈 문자열('')이 포함되므로 예외 처리한다. 1은 소수가 아니므로 1이 아니면서 소수인 경우 cnt를 증가시킨다.

import math
def is_prime_number(x):
    for i in range(2, int(math.sqrt(x)) + 1):
        if x % i == 0:
            return False
    return True

def solution(n, k):
    # 1. 진수 변환
    arr = []
    while n != 0:
        n, r = divmod(n, k)
        arr.append(r)
    arr.reverse()
    # 2. split
    result = ' '.join(str(s) for s in arr)
    result = result.replace(" ", "")
    result = result.split('0')
    # 3. 소수 판별
    cnt = 0
    for i in result:
        if i == '':
            pass
        else:
            p = int(i)
            if p != 1 and is_prime_number(p):
                cnt += 1
    return cnt

👀 참고 자료

• 37강 소수 판별 알고리즘