Fisher Information

Hohyun Kim·2022년 7월 26일
FIMFisher InformationKL-Divergencescore function
1
post-thumbnail

이 글은 지속적으로 수정 및 업데이트 중에 있습니다. 마지막 업데이트: 2022-07-31

통계에서 Fisher information은 파라미터의 신뢰구간을 구할 때 등장하는 개념입니다. 머신러닝과 관련해서는 최적화를 할 때나 뉴럴 네트워크의 성질을 분석할 때 등장합니다. 통계적 모델(선형 모델)이든 뉴럴 네트워크든, negative log likelihood를 손실함수로 두고 이를 최소화하는 방식으로 훈련하는 경우가 많습니다. 그렇기에 log likelihood와 관련한 개념인 Fisher information이 중요한 것입니다.

Definition

Fisher information은 score function의 분산입니다. 만약 score function이 벡터라면 Fisher information은 공분산 행렬입니다. 그러므로 score function이 무엇인지 먼저 알아보겠습니다.

θ\theta를 파라미터로 가진 확률 분포를 pθp_\theta로 나타내겠습니다. NN개의 iid인 데이터가 있다고 할 때, log likelihood는 다음과 같습니다.

L(θ)=∑i=1nlog⁡pθ(xi)L(\theta) =\sum_{i=1}^n\log p_\theta(x_i)

Score function은 log likelihood의 그레디언트입니다.
(s(θ)s(\theta)는 열벡터입니다.)

s(θ)=∇θ∑i=1nlog⁡pθ(xi)=∑i=1n∇θlog⁡pθ(xi)\begin{aligned} s(\theta) &= \nabla_\theta \sum_{i=1}^n\log p_\theta(x_i) \\ &= \sum_{i=1}^n \nabla_\theta\log p_\theta(x_i) \end{aligned}

그림으로 보자면 아래와 같습니다. Log likelihood가 파라미터에 대한 함수로 표현된 그래프(노란 선)으로 나타나 있습니다. 해당 그래프의 기울기가 바로 score입니다.

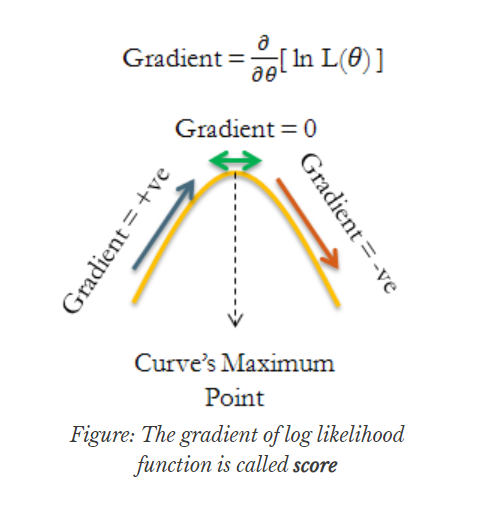
Score function이 log⁡pθ(xi)\log p_\theta(x_i)의 합이므로, Central Limit Theorem에 따라 score function은 asymtotic하게 정규분포를 따릅니다.

s(θ)∼N(0,Σ)s(\theta) \sim \mathcal N(0, \Sigma)

여기서 공분산 행렬은 미지수므로 Σ\Sigma라고 썼는데, 평균은 0이라고 명시했습니다. 어째서 score의 평균이 0이 되는지를 보겠습니다.

Score function의 평균은 0입니다.

proof.

식을 간단히 쓰기 위해 pθ(x)p_\theta( x)가 모든 관측값 xix_i들의 결합분포(joint probability)를 나타낸다고 생각하겠습니다. 그러면 score function은 s(θ)=∇θlog⁡pθ(x)s(\theta)=\nabla_\theta\log p_\theta(x)가 됩니다.

Ex∼pθ[∇θlog⁡pθ(x)]=∑x∇θpθ(x)pθ(x)pθ(x)=∑x∇θpθ(x)=∇θ∑xpθ(x)=0\begin{aligned} E_{x \sim p_\theta} [\nabla_\theta\log p_\theta(x)] &= \sum_x \frac{\nabla_\theta p_\theta(x)}{p_\theta(x)}p_\theta(x) \\ &= \sum_x \nabla_\theta p_\theta(x) \\ &= \nabla_\theta \sum_x p_\theta(x) \\ &= 0 \end{aligned}

마지막 등식에서는 확률 분포의 합이 1이 된다는 성질을 이용했습니다.

한편 Fisher information은 score function의 공분산으로 정의하기 때문에 Σ\Sigma가 Fisher information이라 할 수 있습니다. 그 외에도 다음 세 가지가 (사소한 조건 하에서) 모두 Fisher information과 동일합니다.

  • Score function의 covariance matrix
  • Negative log likelihood의 expected Hessian matrix
  • KL-divergence의 Hessian matrix

각각에 대해 순서대로 알아보겠습니다.

Variance of Score Function

Fisher information은 score function의 분산입니다. 만약 score function이 벡터라면 Fisher information은 공분산 행렬이 됩니다. Fisher information은 II라고 쓰면 다음과 같습니다.

I(θ)=Ex∼pθ[(s(θ)−0)(s(θ)−0)T]=Ex∼pθ[∇θlog⁡pθ(x)∇θlog⁡pθ(x)T]\begin{aligned} I(\theta) &= E_{x \sim p_\theta}[(s(\theta)-0)(s(\theta)-0)^T] \\ &= E_{x \sim p_\theta}[\nabla_\theta\log p_\theta( x)\nabla_\theta\log p_\theta( x)^T] \end{aligned}

I(θ)I(\theta)는 입력값 xx의 구체적인 값에 따라 달라지는 값이 아닙니다. 어차피 xx의 기댓값을 보는 것이기 때문입니다. 하지만 데이터 개수 nn에 따라 크기가 달라집니다. 데이터가 iid므로 Fisher information을 첫 번째 데이터 x1x_1에 대한 log likelihood와 관련된 식으로 나타낼 수 있습니다.

I(θ)=Ex∼pθ[(∑i=1n∇θlog⁡pθ(xi))(∑i=1n∇θlog⁡pθ(xi))T]=nEx1∼pθ[∇θlog⁡pθ(x1)∇θlog⁡pθ(x1)T]=nI1(θ)\begin{aligned} I(\theta) &= E_{x \sim p_\theta}[\big(\sum_{i=1}^n\nabla_\theta\log p_\theta(x_i)\big) \big(\sum_{i=1}^n\nabla_\theta\log p_\theta(x_i)\big)^T] \\ &= nE_{x_1 \sim p_\theta}[\nabla_\theta\log p_\theta(x_1)\nabla_\theta\log p_\theta(x_1)^T] \\ &= nI_1(\theta) \end{aligned}

어차피 스케일 차이므로 I1(θ)I_1(\theta)를 Fisher information이라고 하기도 합니다. 이 글에서는 앞으로 I1(θ)=FθI_1(\theta) = F_\theta로 쓰고, FθF_\theta를 Fisher information이라고 하겠습니다. (FF나 II 모두 Fisher information을 나타내는 기호로 많이 사용합니다.)

Expected Hessian of NLL

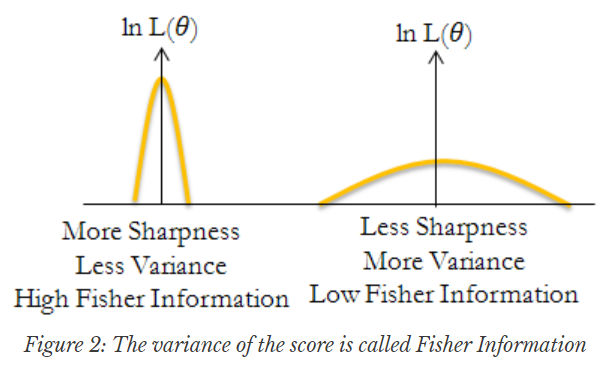
Fisher information을 다른 방식으로 정의할 수 있습니다. 바로 negative log likelihood(NLL)의 expected Hessian입니다.

Fθ=Ex∼pθ[−∇θ2log⁡pθ(x)]F_\theta = E_{x \sim p_\theta}[-\nabla_\theta^2 \log p_\theta( x)]

Score function의 공분산 행렬과 negative log likelihood의 expected Hessian이 같음을 증명할 수 있습니다.

Score function의 공분산 행렬과 negative log likelihood의 expected Hessian은 같습니다.

proof.

Log likelihood를 두 번 미분해서 식을 정리해보면 다음과 같습니다.

∇θ2log⁡pθ(x)=Jθ(∇θpθ(x)pθ(x))=∇θ2pθ(x)pθ(x)−(∇θpθ(x)pθ(x))(∇θpθ(x)pθ(x))T=∇θ2pθ(x)pθ(x)−∇θlog⁡pθ(x)∇θlog⁡pθ(x)T\begin{aligned} \nabla_\theta^2 \log p_\theta( x) &= \text{J}_\theta\bigg(\frac{\nabla_\theta p_\theta( x)}{p_\theta( x)} \bigg) \\ &= \frac{\nabla_\theta^2 p_\theta( x) }{p_\theta( x)} - \bigg(\frac{\nabla_\theta p_\theta( x)}{p_\theta( x)} \bigg)\bigg(\frac{\nabla_\theta p_\theta( x)}{p_\theta( x)}\bigg)^T \\ &= \frac{\nabla_\theta^2 p_\theta( x) }{p_\theta( x)} -\nabla_\theta\log p_\theta( x)\nabla_\theta\log p_\theta( x)^T \end{aligned}

위에서 Jθ\text{J}_\theta는 Jacobian matrix를 만드는 연산입니다. 위 결과에서 양변에 expectaion을 취하면 원하는 결과를 얻을 수 있습니다. expectation의 결과 마지막 식에서 pθp_\theta의 Hessian은 0이 되어 사라지기 때문입니다.

Ex∼pθ[∇θ2pθ(x)pθ(x)]=∑x∇θ2pθ(x)=0\begin{aligned} E_{ x \sim p_\theta} \bigg[\frac{\nabla_\theta^2 p_\theta( x) }{p_\theta( x)} \bigg] = \sum_{ x} \nabla_\theta^2 p_\theta( x) = 0 \end{aligned}

여기서도 확률분포의 합은 1이라는 점, 그리고 ∑\sum 기호와 ∇θ2\nabla_\theta^2를 바꾸는 트릭을 이용했습니다.

FθF_\theta은 log likelihood function이 파라미터 공간 상에서 휘어진 정도를 측정합니다. 휘어짐이 심한 부분일수록 해당 방향으로 손실함수가 민감하게 반응한다는 의미입니다. 이 때문에 Natural Gradient에서는 경사하강법을 실시할 때 그레디언트에 Fθ−1F_\theta^{-1}을 곱해서 업데이트를 실시합니다.

Hessian of KL-divergence

Fisher information을 다르게 이해하는 방법은 Fisher information을 KL-divergence의 Hessian으로 보는 것입니다.

θ\theta와 θ′\theta'을 파라미터로 가지는 확률분포를 각각 pθp_\theta와 pθ′p_{\theta'}이라 하겠습니다. KL-divergence는 다음과 같습니다.

DKL(θ∣∣θ′)=Ex∼pθ[log⁡pθ(x)−log⁡pθ′(x)]D_{KL}(\theta || \theta') = E_{x \sim p_\theta}[\log p_\theta(x) - \log p_{\theta'}(x)]

DKL(θ∣∣θ′)D_{KL}(\theta || \theta')와 DKL(θ′∣∣θ)D_{KL}(\theta' || \theta)는 같지 않습니다. 그럼에도 다음이 성립합니다.

Fθ=∇θ′2DKL(θ∣∣θ′)∣θ′=θ=∇θ′2DKL(θ′∣∣θ)∣θ′=θ\begin{aligned} F_\theta &= \nabla_{\theta'}^2D_{KL}(\theta || \theta') |_{\theta' = \theta} \\ &= \nabla_{\theta'}^2D_{KL}(\theta' || \theta) |_{\theta' = \theta} \end{aligned}

KL-divergence의 Hessian이 Fisher information이라는 성질 때문에 Fisher information을 이용해 KL-divergence를 근사할 수 있습니다.

DKL(θ′∣∣θ)≈12(θ−θ′)TFθ(θ−θ′)  DKL(θ∣∣θ′)≈12(θ−θ′)TFθ(θ−θ′)D_{KL}(\theta' || \theta) \approx \frac{1}{2} (\theta - \theta')^T F_\theta (\theta - \theta') \\ \; \\ D_{KL}(\theta || \theta') \approx \frac{1}{2} (\theta - \theta')^T F_\theta (\theta - \theta') \\

이는 KL-divergence를 θ′\theta'에서 Taylor 전개해보면 알 수 있습니다.

θ\theta와 θ′\theta'이 비슷한 경우 Fisher information matrix를 이용해 KL-divergence를 근사할 수 있습니다.

proof.

한쪽 방향만 증명해보겠습니다. DKL(θ∣∣θ′)D_{KL}(\theta || \theta')를 2차 Taylor 전개로 근사하면 다음과 같습니다.

DKL(θ∣∣θ′)≈DKL(θ′∣∣θ′)+∇θDKL(θ∣∣θ′)T(θ−θ′)+12(θ−θ′)TFθ(θ−θ′)D_{KL}(\theta || \theta') \approx D_{KL}(\theta' || \theta') + \nabla_\theta D_{KL}(\theta || \theta')^T(\theta - \theta') + \frac{1}{2} (\theta - \theta')^T F_\theta (\theta - \theta')

위에서 DKL(θ′∣∣θ′)D_{KL}(\theta' || \theta')는 같은 분포 간의 KL-divergence므로 0이 됩니다.
KL-divergence의 그레디언트를 구하면 다음과 같습니다.

∇θDKL(θ∣∣θ′)=∇θ∑xpθ(x)log⁡pθ(x)pθ′(x)=∑x∇θpθ(x)[1+log⁡pθ−log⁡pθ′]=∑x∇θpθ(x)[log⁡pθ−log⁡pθ′]\begin{aligned} \nabla_\theta D_{KL}(\theta || \theta') &= \nabla_\theta \sum_x p_{\theta}(x)\log\frac{p_{\theta}(x)}{p_{\theta'}(x)} \\ &= \sum_x \nabla_\theta p_{\theta}(x) [1 + \log p_{\theta} - \log p_{\theta'}] \\ &= \sum_x \nabla_\theta p_{\theta}(x) [\log p_{\theta} - \log p_{\theta'}] \end{aligned}

마지막 1은 pθp_\theta가 확률분포므로 없앨 수 있습니다. 마찬가지로 θ\theta가 어떤 값을 가지든 log⁡pθ−log⁡pθ′\log p_{\theta} - \log p_{\theta'}는 상수가 되어 사라집니다.

Fisher information matrix의 특징 중 하나는 positive semi-definite이라는 점입니다. 이는 FIM이 outer product (∇θlog⁡pθ(x)∇θlog⁡pθ(x)T\nabla_\theta\log p_\theta(x)\nabla_\theta\log p_\theta(x)^T)의 기댓값이라는 점에서나, 공분산 행렬이라는 점에서나, 또는 DKLD_{KL}의 값이 0 이상이라는 점에서도 알 수 있습니다.

Empirical Fisher

Fisher information은 ∇θlog⁡pθ(x)∇θlog⁡pθ(x)T\nabla_\theta\log p_\theta( x)\nabla_\theta\log p_\theta( x)^T의 기댓값이므로 다음과 같이 샘플을 이용해서 근사를 할 수 있다고 설명하고 이를 Empirical Fisher라고 부르기도 합니다.

1n∑i=1n∇θlog⁡pθ(xi)∇θlog⁡pθ(xi)T\frac{1}{n}\sum_{i=1}^n \nabla_\theta\log p_\theta(x_i)\nabla_\theta\log p_\theta( x_i)^T

그러나 위 식은 데이터 분포로부터 추출된 샘플을 이용한 것입니다. 즉

Ex∼pθ[∇θlog⁡pθ(x)∇θlog⁡pθ(x)T]≠Ex∼Data[∇θlog⁡pθ(x)∇θlog⁡pθ(x)T]E_{x \sim p_\theta} [\nabla_\theta\log p_\theta(x)\nabla_\theta\log p_\theta( x)^T] \neq E_{x \sim Data} [\nabla_\theta\log p_\theta(x)\nabla_\theta\log p_\theta( x)^T]

입니다. Fisher information을 샘플을 이용해 편향 없이 근사하려면, xx를 pθp_\theta에서 추출해야 합니다.

마찬가지 이유로 Fisher information이 negative log likelihood의 Hessian이라는 설명에도 주의가 필요합니다. 위 설명이 맞다면 뉴럴 네트워크 손실값의 Hessian이 곧 Fisher information matrix고, Fisher information matrix는 positive semi-definite이므로 뉴럴 네트워크는 convex하다는 뜻이 됩니다. 그러나 뉴럴 네트워크는 convex가 아니죠.

Empirical Fisher가 좋은 근사가 되려면 pθp_\theta가 데이터 분포와 비슷해야 합니다. 만약 training loss가 최솟값 근처면 Empirical Fisher는 true Fisher의 비편향 추정량이 되며, 뉴럴 네트워크 손실값에 대한 Hessian이 곧 Fisher가 됩니다.

이와 관련한 보다 자세한 논의는 "Limitations of the Empirical Fisher Approximation for Natural Gradient Descent"를 보시기 바랍니다. 여러 논문과 구현에서 empirical Fisher를 부주의하게 사용하는 데 대해 주의를 요하고 있는 논문입니다.

Summary

정리하자면 다음은 모두 Fisher information과 같습니다.

  • Score function의 covariance matrix
  • Negative log likelihood의 expected Hessian matrix
  • KL-divergence의 Hessian matrix

Fisher information은 항상 positive semi-definite합니다.

Reference

profile
Hohyun Kim
vegan, data scientist, effective altruist
이전 포스트

TRPO 구현을 위해 알야야 할 것들

1개의 댓글

comment-user-thumbnail
BS C
2024년 4월 10일

글 잘 읽었습니다. 논문 읽다가 너무 생소한 개념이 나와서 당황했는데, 글덕분에 많이 배워가요!

답글 달기