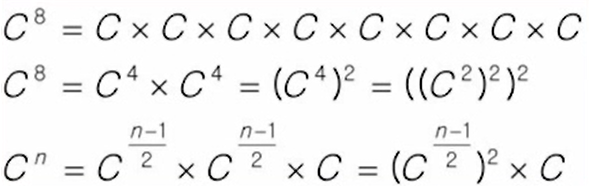📖 분할정복

---

정의

• 큰 문제를 작은 문제로 쪼개어 해결해 나가는 방식

설계 전략

• 분할(Divide): 해결할 문제를 여러개의 작은 부분으로 나눔
• 정복(Conquer): 나눈 작은 문제를 각각 해결
• 통합(Combine): 해결된 해답을 모음

💬 응용 : 거듭 제곱

---

반복문 알고리즘: O(n)

재귀 알고리즘: O(n)

분할 정복 알고리즘: O(log2N)

• 짝수일 때와 홀수일 때 나누어서 생각

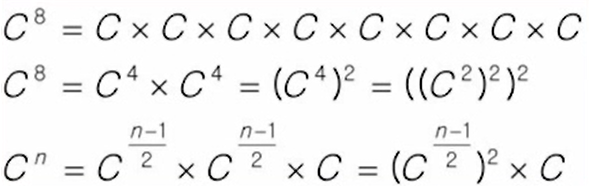
💬 응용 : 병합 정렬

---

정의

• 여러 개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방식

활용 방식

• 자료를 최소 단위의 문제까지 나눈 후 차례대로 정렬하여 최종 결과 얻음

시간 복잡도 : O(n log n)

◾ 병합 정렬 과정

• [ 69, 10, 30, 2, 16, 8, 31, 22 ]를 병합 정렬하는 과정

1. 분할 단계

• 전체 자료 집합에 대해, 최소 크기의 부분집합이 될 때까지 분할
  

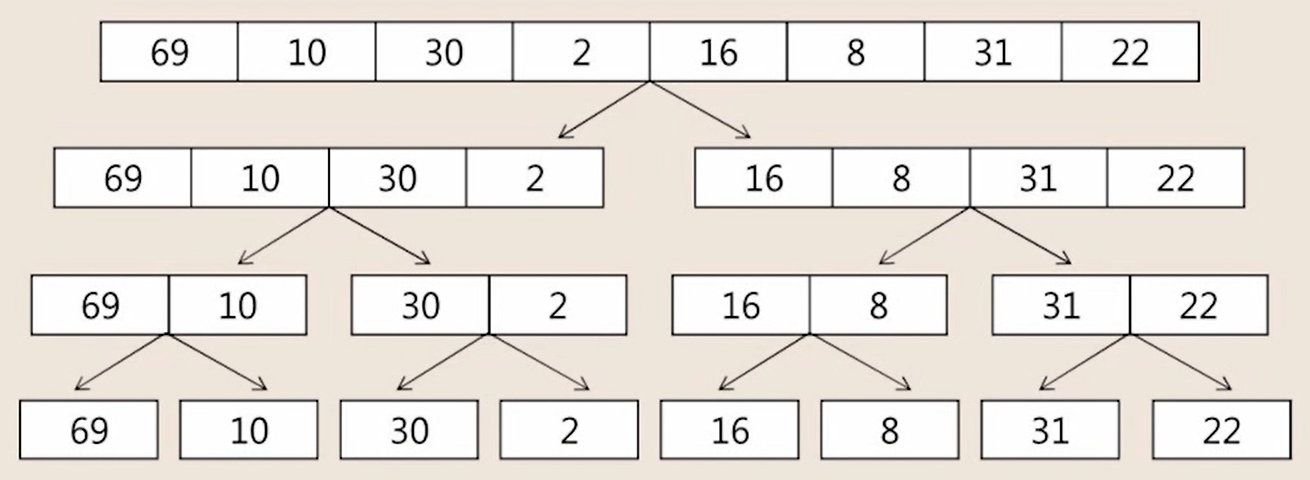
2. 병합 단계

• 2개의 부분집합을 정렬하면서 하나의 집합으로 병합
  

병합 정렬 알고리즘

• 참고 설명

public class 병합정렬 {

	public static void main(String[] args) {
		int[] arr = {69, 10, 30, 2, 16, 8, 31, 22};
		int[] tmp = new int[arr.length];

		mergeSort(arr, tmp, 0, arr.length-1);
		
		for(int i : arr)
			System.out.println(i);
	}
	
	// 배열, 인덱스 0, 인덱스 마지막
	static void mergeSort(int[] arr, int[] tmp, int start, int end) { 
		
		if(start < end) {
			int mid = (start + end) / 2;
			
			mergeSort(arr, tmp, start, mid); // 왼쪽 계속 분할
			mergeSort(arr, tmp, mid+1, end); // 오른쪽 계속 분할
			
			int startL = start, startR = mid+1; // 두 분할 원소의 첫번째 인덱스
			int idx = startL; // 비교하는 배열의 저장 첫위치 = 왼쪽 배열 첫위치
			
			while(startL <= mid || startR <= end) {
				if(startR > end // 오른쪽 분할 원소를 이미 다 가져왔을 때
						// 왼쪽 분할에서 가져오지 않은 원소가 있고
						// 왼쪽 분할의 첫 원소 값이 오른쪽 분할의 첫 원소 값보다 작을 때
						|| (startL <= mid && arr[startL] < arr[startR])) 
					tmp[idx++] = arr[startL++];
				
				else tmp[idx++] = arr[startR++];
				
			}
			
			// 정렬된 값 저장
			for (int i = start; i <= end; i++) {
				arr[i] = tmp[i];
			}
			
		}
	}

}

💬 응용 : 퀵 정렬

---

정의

• 주어진 배열을 두 개로 분할 수 각각 정렬

병합 정렬과 차이점

• 병합정렬은 그냥 두 부분으로 나누는 반면, 퀵 정렬을 분할 시 기준 아이템 중심으로 위치 시킴
• 각 부분 정렬이 끝난 후 병합정렬은 '병합'이란 후처리 작업 필요, 하지만 퀵정렬은 필요 없음

시간 복잡도 : O(n log n)

◾ 아이디어

P(피봇)값들 보다 큰 값은 오른쪽, 작은 값은 왼쪽 집합에 위치

• 오름차순 기준시

P를 두 집합의 가운데 위치

피봇 선택 방법

• 왼쪽 끝 / 오른쪽 끝 / 임의의 세 개 값 중 중간값
• 일반적으로 왼쪽 끝으로 많이 함

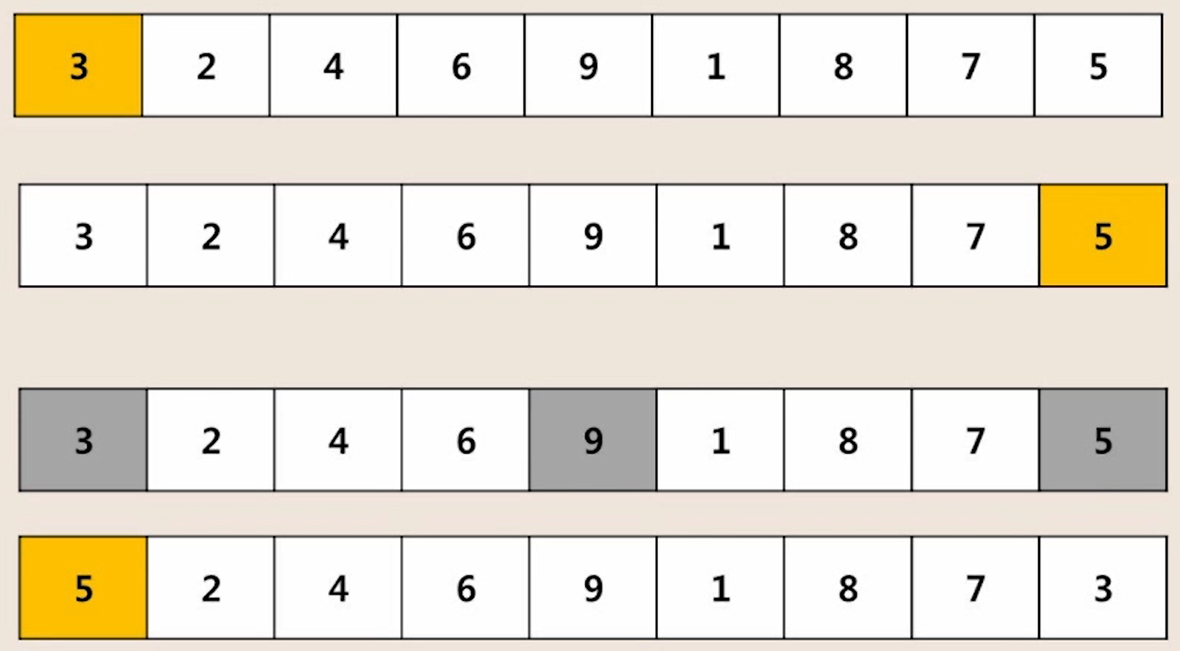
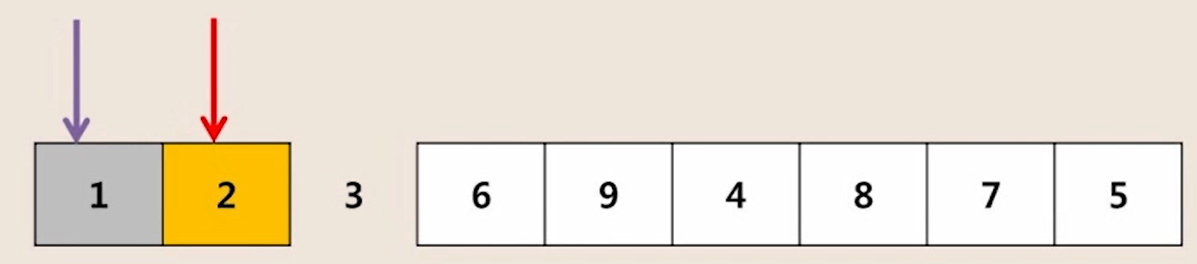
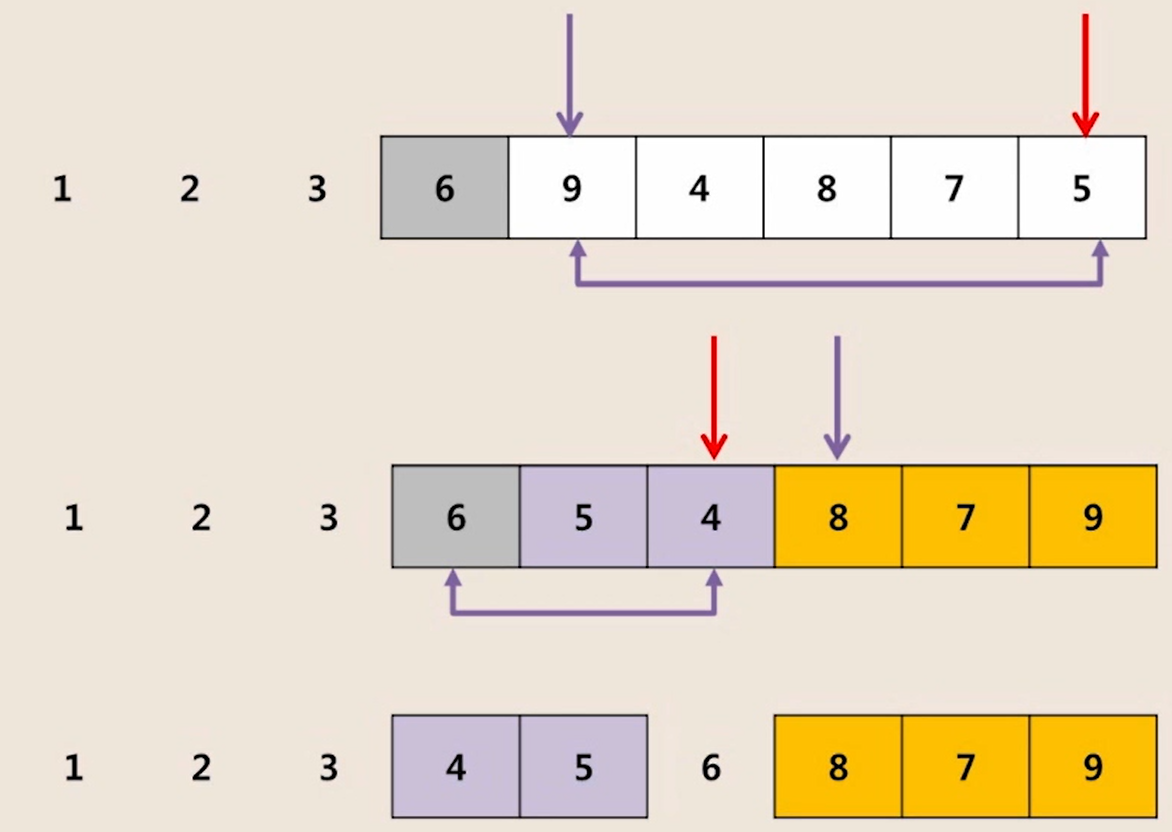
◾ 퀵 정렬 과정

• [ 3, 2, 4, 6, 9, 1, 8, 7, 5 ] 를 퀵 정렬하는 과정

1. i 인덱스, j 인덱스 순차적으로 비교하며 조건에 안맞는 숫자 찾기

• i 인덱스 : 피봇보다 큰 값 찾아야 함
• j 인덱스 : 피봇보다 작은 값 찾아야 함

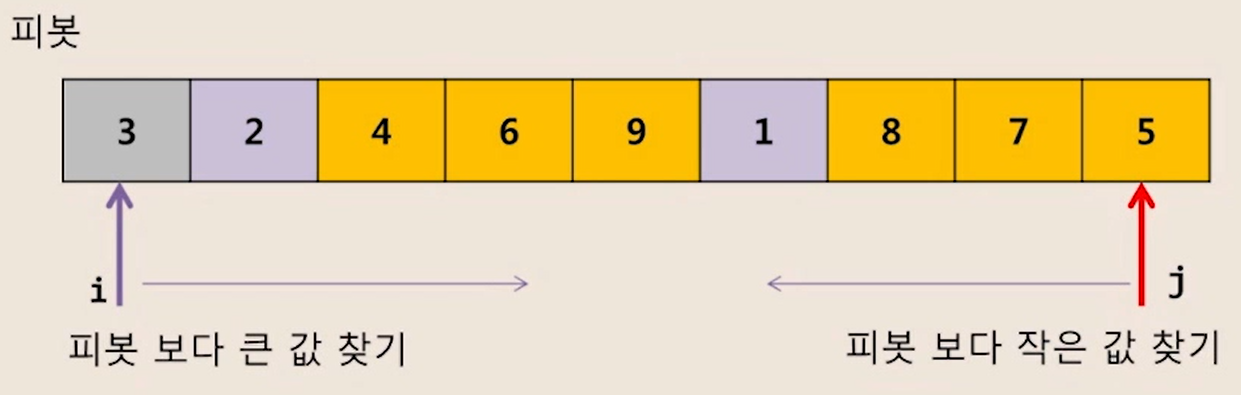
2. 조건이 안맞는 두 수 위치 교환

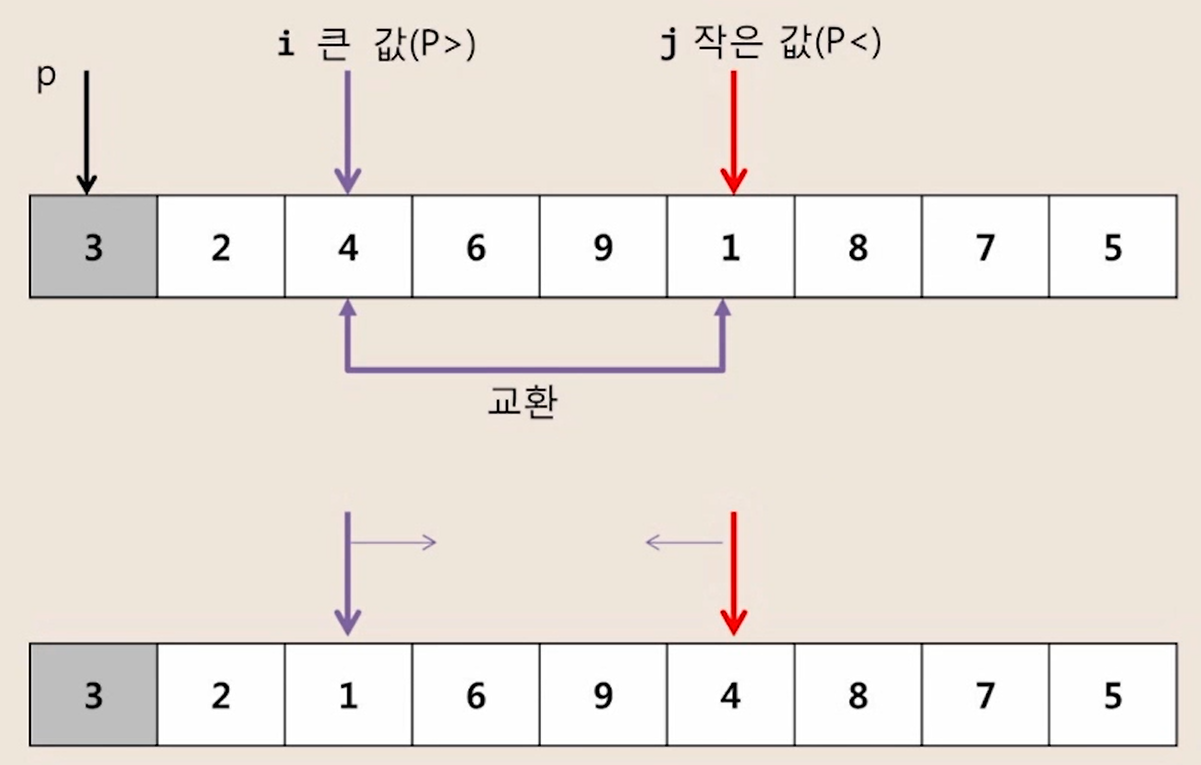
3. i와 j가 교차할 때, j와 피봇 위치 교환

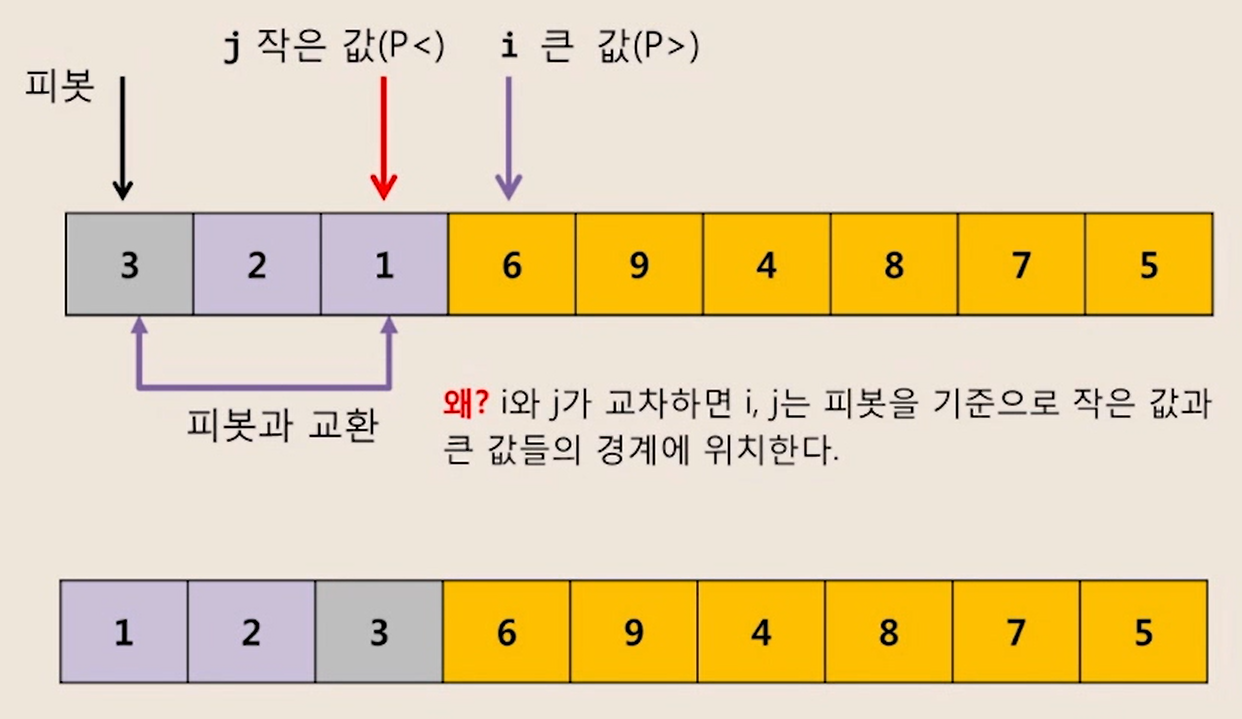
4. 다시 위 과정 반복

• 왼쪽 배열은 위치 변환 없음
  
• 오른쪽 배열의 피봇 6 중심으로 진행
  

◾ 퀵 정렬 알고리즘

public class 퀵정렬 {

	public static void main(String[] args) {
		int[] arr = {3, 2, 4, 6, 9, 1, 8, 7, 5};

		quickSort(arr, 0, arr.length-1);
		for(int i : arr)
			System.out.println(i);
	}
	
	static void quickSort(int[] arr, int start, int end) {
		if(start < end) {
			int p = start, i = start+1, j = end;
			
			while(i <= j) { // 교차하면 끝남
				while(arr[i] <= arr[p]) i++; // 피벗보다 작을 때 진행
				while(arr[j] > arr[p]) j--; // 피벗보다 클 때 진행
				
				if(i < j) { // 아직 교차하지 않았을 때 교환
					int tmp = arr[i];
					arr[i] = arr[j];
					arr[j] = tmp;
				}
			}
			
			// j와 피벗의 위치 교환
			int tmp = arr[p];
			arr[p] = arr[j];
			arr[j] = tmp;
			
			// 왼쪽 배열, 오른쪽 배열 나눠서 다시 진행
			quickSort(arr, start, j-1);
			quickSort(arr, j+1, end);
		}
	}
}