https://school.programmers.co.kr/learn/courses/30/lessons/118669

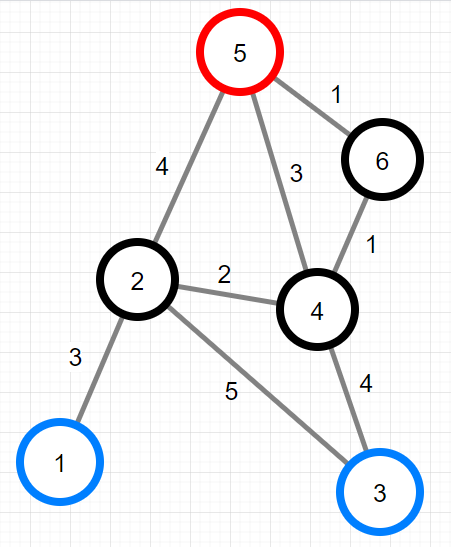
이렇게 생긴 그래프가 있고 파란색이 출입구, 빨간색이 정상일 때, 등산 코스를 이루는 각 경로의 거리가 최소값인 등산코스 찾는 문제이다.

정상은 한 번만 가야하고, 들어갔던 출입구로 나와야한다.

Python

시도 1 - 실패

from heapq import heappush, heappop
from collections import defaultdict

def solution(n, paths, gates, summits):
    answer = [float('inf'), float('inf')]
    
    gates_set = set(gates)
    summits_set = set(summits)
    # 거리 합이 최소가 아니라도
    # 거리 한 개의 길이가 최대인게 최소가 되게 해라는거네
    
    graph = defaultdict(list)
    for a, b, c in paths:
        graph[a].append((b, c))
        graph[b].append((a, c))
    
    for g in gates:
        intensity = [-1] * (n + 1)
        q = [(0, g, False)] # 정상에 닿았는가
        intensity[g] = 0
        
        while q:
            cost, now, summit_chk = heappop(q)
            
            # g에서 출발했는데 다른 게이트 있으면 안 됨
            if now != g and now in gates_set:
                continue
                
            # 정상에 닿았는데 다른 정상에 가면 안 됨
            if summit_chk and now in summits_set:
                continue
            
            # 이미 찾은 거리가 새로 계산할 거리보다 작다면 패스
            if 0 <= intensity[now] < cost:
                continue
            
            for next, d in graph[now]:
                if intensity[next] == -1 or intensity[next] > cost:
                    # 거리합이 중요한 것이 아니라 거리가 중요한거라 더하기 안 하고 그냥 작은 거리로 업데이트 할 것
                    intensity[next] = max(cost, d)
                    if next in summits_set:
                        summit_chk = True
                    heappush(q, (intensity[next], next, summit_chk))
        for s in summits:
            if intensity[s] < answer[1]:
                answer = [s, intensity[s]]
            elif intensity[s] == answer[1] and (s < answer[0]):
                answer[0] = s
    return answer

gate별로 시작하면서 다익스트라를 돌렸다. 등산코스 경로의 최대값을 저장하는 intensity를 만들어서 그거를 기준으로 heap을 만들었다.
다른 출입구에 닿지 않게 조건을 추가하였고, 다른 정상도 안 가게 summit_chk를 만들어서 정상에 닿은 코스일 경우 True를 저장해서 다른 정상에 못 가게 했다.

그리고 다익스트라가 끝나면 intensity가 최소인 정상, 그리고 값이 같으면 정상 번호가 작은 것을 저장하게 했는데 일부 시간초과와 일부 그냥 실패가 결과로 나왔다.

아무래도 모든 게이트에 대해서 모든 정상까지의 거리를 비교한게 시간초과의 원인이 된 것 같다.

시도 2 - 실패

from heapq import heappush, heappop
from collections import defaultdict

def solution(n, paths, gates, summits):
    answer = [float('inf'), float('inf')]
    
    gates_set = set(gates)
    summits_set = set(summits)
    
    graph = defaultdict(list)
    for a, b, c in paths:
        graph[a].append((b, c))
        graph[b].append((a, c))
    
    for g in gates:
        intensity = [-1] * (n + 1)
        q = [(0, g)]
        intensity[g] = 0
        
        while q:
            cost, now = heappop(q)
            
            if (now != g and now in gates_set) or 0 <= intensity[now] < cost:
                continue
            
            for next, d in graph[now]:
                if intensity[next] == -1 or intensity[next] > max(d, cost):
                    intensity[next] = max(cost, d)
                    if next not in summits_set:
                        heappush(q, (intensity[next], next))
                    else:
                        if intensity[next] < answer[1]:
                            answer = [next, intensity[next]]
                        elif intensity[next] == answer[1] and (next < answer[0]):
                            answer[0] = next
            
    return answer

answer에 값을 비교하는 과정을 다익스트라 안에 넣었다.
정상에 도착하면 heap에 넣는 대신 answer에 거리와 정상 번호를 비교해서 업데이트 하도록 했고, 정상이 아닐 경우에만 que에 해당 지점을 넣었다.

이렇게하니까 15, 16, 17, 23, 25에서 시간초과 발생한 것 외에 전부 정답처리되었다.

시도 3

from heapq import heappush, heappop
from collections import defaultdict

def solution(n, paths, gates, summits):
    answer = [float('inf'), float('inf')]
    
    gates_set = set(gates)
    summits_set = set(summits)
    
    graph = defaultdict(list)
    for a, b, c in paths:
        graph[a].append((b, c))
        graph[b].append((a, c))
    
    q = []
    intensity = [-1] * (n + 1)
    for g in gates:
        heappush(q, (0, g))
        intensity[g] = 0
    
    while q:
        cost, now = heappop(q)

        if (cost != 0 and now in gates_set) or 0 <= intensity[now] < cost:
            continue

        for next, d in graph[now]:
            if intensity[next] == -1 or intensity[next] > max(d, cost):
                intensity[next] = max(cost, d)
                if next not in summits_set:
                    heappush(q, (intensity[next], next))
                else:
                    if intensity[next] < answer[1]:
                        answer = [next, intensity[next]]
                    elif intensity[next] == answer[1] and (next < answer[0]):
                        answer[0] = next
            
    return answer

GPT의 도움을 받아 해결했다. 이전 코드처럼 게이트 하나당 다익스트라를 실행하지 않고 동시에 여러 게이트에 대해서 다익스트라를 진행할 수 있었다.
대신, 이렇게하면 어떤 시작점에 대한 최소거리인지 알 수 없게 되는데 어차피 문제에서는 정상과 정상까지의 최단거리만을 요구하였기에 시작점을 알 필요가 없다.

여러 시작점에 대한 최단거리를 구해야할 때, 시작점의 구분이 중요하지 않다면 그냥 heap에 시작점 다 넣고 시작하는 다익스트라를 고려해봐야겠다.