최소 신장 트리
신장 트리 (Spanning Tree)
: 그래프 내의 모든 정점을 포함하는 트리
모든 정점이 연결되어 있고, 사이클이 없는 그래프이다.
신장 트리는 n개의 정점을 (n-1)개의 간선으로 표현한다.
신장 트리 == 그래프의 최소 연결 부분 그래프
최소 신장 트리 (MST : Minimum Spanning Tree)
: 간선들의 가중치의 합이 최소인 신장트리.
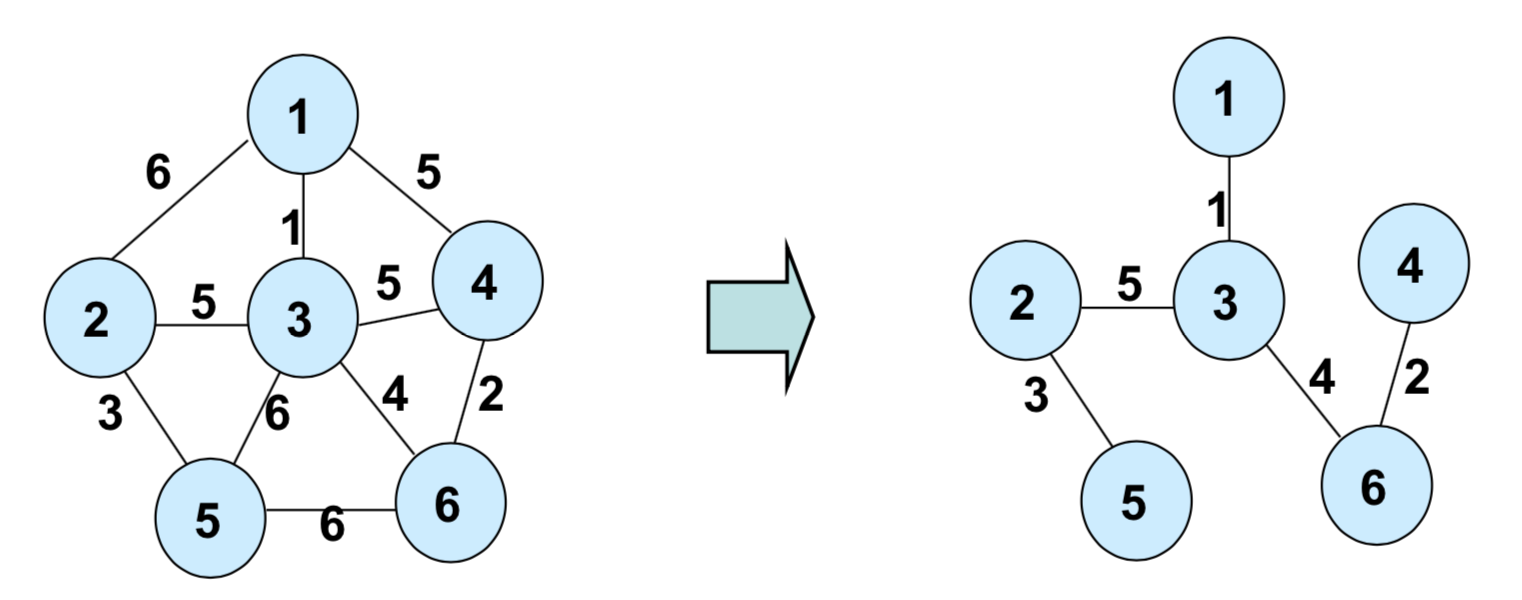
위 그래프에서 오른쪽의 트리가 최소 신장 트리이다.
최소 신장트리가 되기 위한 조건
-
간선의 개수 = 정점의 개수 - 1
(정점 n, 간선 e일 때e = n - 1 -
사이클이 없다.
-
가중치의 합이 최소
최소 신장 트리 (이하 MST)를 구하기 위한 알고리즘은 크게 두 가지가 있다.
MST 구현 알고리즘
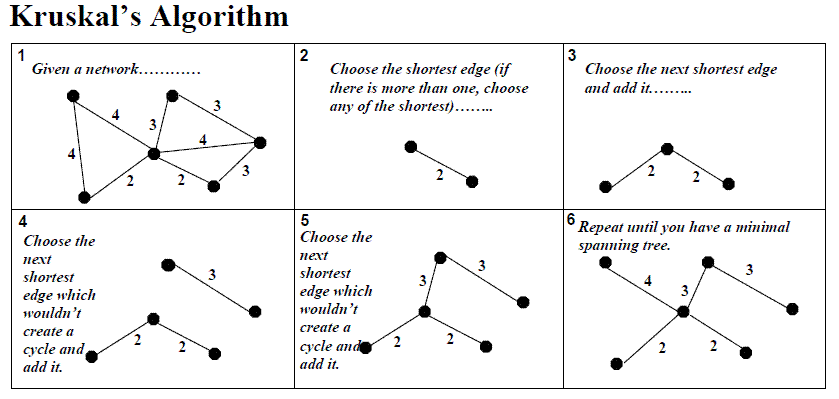
Kruskal 알고리즘
Greedy 한 방법을 이용해서 각 단계 별 최소 비용을 구한다.
Greedy
: 탐욕법
현재 상황에서 가장 최적의 상황만을 찾는다.
구현 방법
각 단계에서 사이클을 이루지 않는 최소 비용의 간선을 선택한다.
- 모든 간선들을 가중치 기준 오름차순으로 정렬한다.
- 가장 가중치가 작은 간선을 선택한다.
- 만약, 그 간선을 선택하면 사이클을 이루는 경우, 해당 간선을 통과하고 다음으로 가중치가 작은 간선을 선택한다.
여기서 해당 간선이 사이클을 이루는지 여부는, union-find 알고리즘을 이용해서 판별한다.
union-find 알고리즘
여러 정점 중에서, 두 정점이 속하는 집합이 같은 집합인지 판별한다.
(정점 u, v에 대해 u가 속한 집합과 v가 속한 집합이 같은 집합인지)union-find = union + find 연산.
union: 두 원소가 속한 집합을 합치는 연산 (합집합)
find: 해당 원소가 속한 집합을 반환하는 연산
시간복잡도
정점 n개, 간선 e개 라고 했을 때
간선들을 정렬해야 하므로
시간 복잡도는 O(eloge).
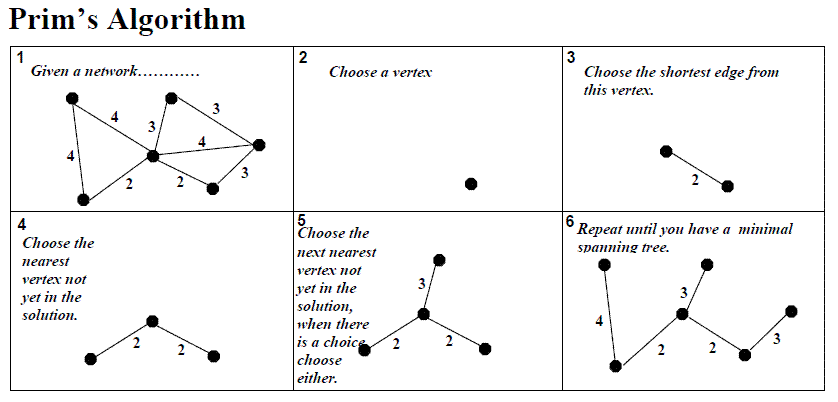
Prim 알고리즘
단계 별로, 신장 트리의 집합을 확장시켜 나가는 방법이다.
구현 방법
이전 단계에서 만들어진 신장 트리 집합에서 인접한 정점들 중, 최소 간선으로 연결된 정점을 추가하는 방식이다.
우선순위 큐를 사용한다.
- 시작 정점을 MST 집합에 포함한다.
- 해당 정점에서 가장 작은 가중치로 연결된 정점을 MST 집합에 포함한다.
시간복잡도
정점 n개 기준
O(n^2)
Kruskal vs Prim
둘 다 가중치가 작은 간선들을 Greedy하게 선택한다는 공통점이 있다.
하지만 Kruskal은 간선들을 정렬하고 가중치가 작은 간선부터 선택하고,
Prim은 임의의 정점부터 시작해서, 해당 정점 기준으로 가중치가 가장 작은 간선을 선택해나간다.
| 구분 | Kruskal | Prim |
|---|---|---|
| 기준 | 간선 선택 기반 | 정점 선택 기반 |
| 시간복잡도 | O(eloge) | O(n^2) |
때문에,
정점에 비해 간선이 드문 희박한 그래프라면 Kruskal 알고리즘을 사용하고,
간선이 많은 밀집된 그래프라면 Prim 알고리즘을 사용하는 것이 적합하다.