이번 글에서는 divide & conqure를 더 깊이있게 살펴보기 위해서 matrix multiplaction (이하 matmul)에 대한 알고리즘을 살펴보고자한다. Matmul은 단순히 입력 matrix의 scalar multiplcation & summation을 반복하는 알고리즘이지만, 딥러닝, 지도 어플리케이션, 그래프 알고리즘을 비롯한 다양한 알고리즘에서 적용되는만큼 활용분야가 넓다.
그런데 실제 computer system에 여러 제약사항이 있다보니 이를 효율적으로 수행하기 위한 다양한 알고리즘과 가속기 아키텍처 등이 제안되었다. 접근 방식이 다양하지만 본 글에서는 Strassen's algorithm과 cache efficient algorithm에 대해서 살펴보고자한다. 본 글은 Introduction to algorithm (Thomas H, et. al.)과 MIT 6.172 lecture note를 참고하여 작성되었다.
Matrix Multiplication
 [Simple matrix multiplication code & time complexity]
[Simple matrix multiplication code & time complexity]

Matmul을 divide & conqure로 수행하기 위한 알고리즘은 아래와 같다.


Divide는 의 시간이 걸리고, Conquer는 8개의 sub-matrix에 대해 의 시간이 걸리므로 가 걸린다. Combine은 4개 sub-solution을 합치는 과정으로 사이즈의 4개의 matrix에 대한 시간이므로 의 시간이 소요된다.
이를 나타낸 식이 위의 이 되겠다. Divide & conquer에서와 마찬가지로 master method를 적용하면 이 된다. 따라서 단순히 divide & conqure 알고리즘을 사용하더라도 시간복잡도가 줄어들지 않았다. 그렇다면 어떠한 방식으로 matmul 연산을 효율적으로 수행할 수 있을까?
Strassen's Algorithm
Strassen's 알고리즘은 matmul에서 multiplication을 수행하는 sub-matrix의 수를 8개에서 7개로 줄여서 time complexity를 낮추는 알고리즘이다. Stranssen's 알고리즘도 constant number of addtion/subtraction을 수행하긴해야한다. 다만, matmul에서 중요한 연산은 addition/subtraction이 아닌 multiplication 연산이기 때문에 (sub-matrix의 multiplication은 scalar multiplication과 accumulation 연산을 포함하기 때문) Strassen's 알고리즘이 효율적인 연산을 수행할 수 있는 것이다. Strassen's 알고리즘을 살펴보면 다음과 같다.

Step 2에서 matmul에서 10개의 sub-matrix에 대한 addtion/substitution 연산을 수행하며, 각 sub-matrix에 대한 연산 식은 아래와 같다.
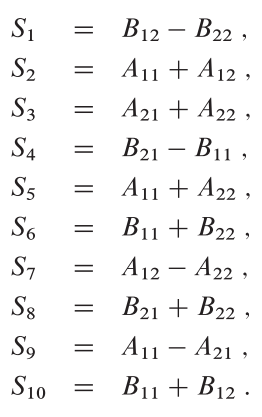

Step 3에서는 Step 2에서 구한 matrix를 & sub-matrix와 multiplication을 수행하여 Partial matrix를 구한다.
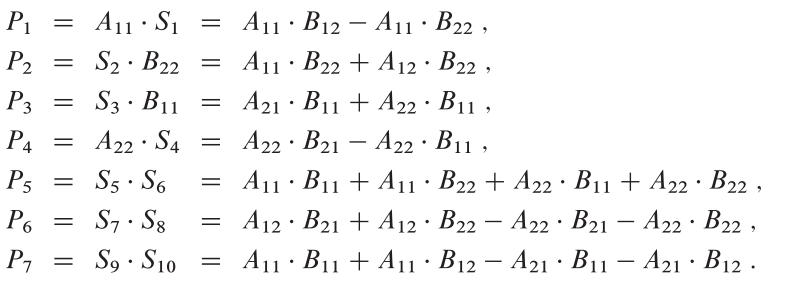
위와 같이 Partial matrix를 구한뒤, final matrix인 matrix를 구하는데 사용한다.
Step 4는 다음과 같다.

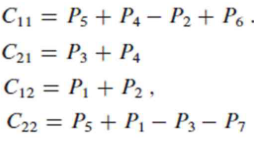
Strassen's 알고리즘의 복잡도는 sub-matrix의 multiplication 와 Step1/2/4에서 수행하는 matrix의 addtion/subtration complexity 에 의해 결정되며 이를 정리하면 다음과 같다.

마찬가지로 master method에 의해 정리하면, Strassen's algorithm의 complexity는 아래와 같다.
.
이렇게 보면 커다란 차이가 아닌것 처럼 보일 수 있지만 matrix size(n)이 증가함에 따라 연산의 수가 크게 차이를 보인다. Strassen's algorithm의 addition을 보다 효율적으로 수행할 수 있는 Winograd algorithm이 존재하는데 이는 딥러닝 프레임워크에도 적용되는 알고리즘이다. 이에 대한 내용은 나중에 정리할 예정이다.
Cache Efficient Algorithm
설명을 살펴보기 전에 몇가지 notation과 terminology를 정리해본다.
Tall Cache
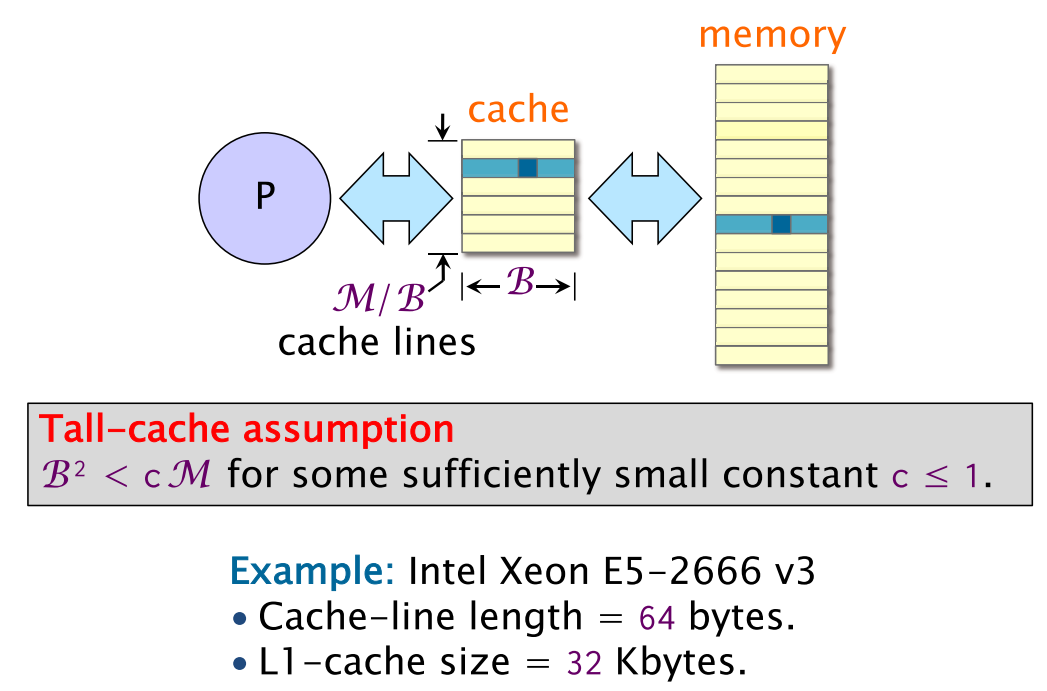
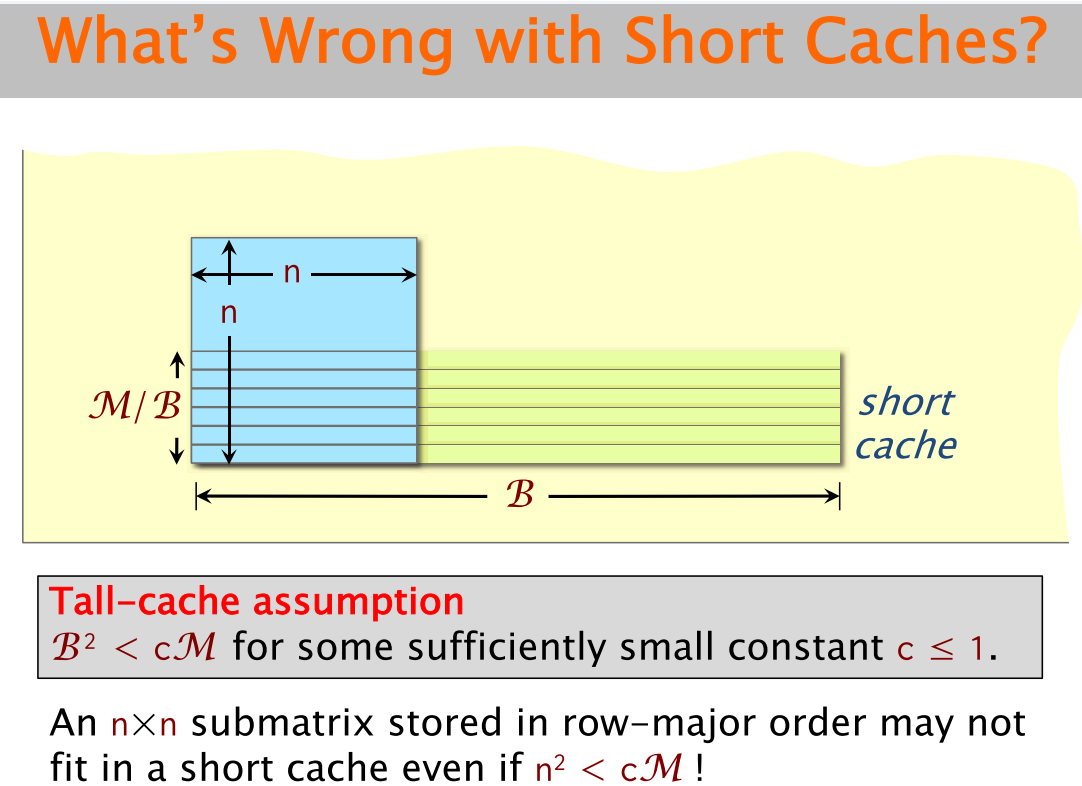
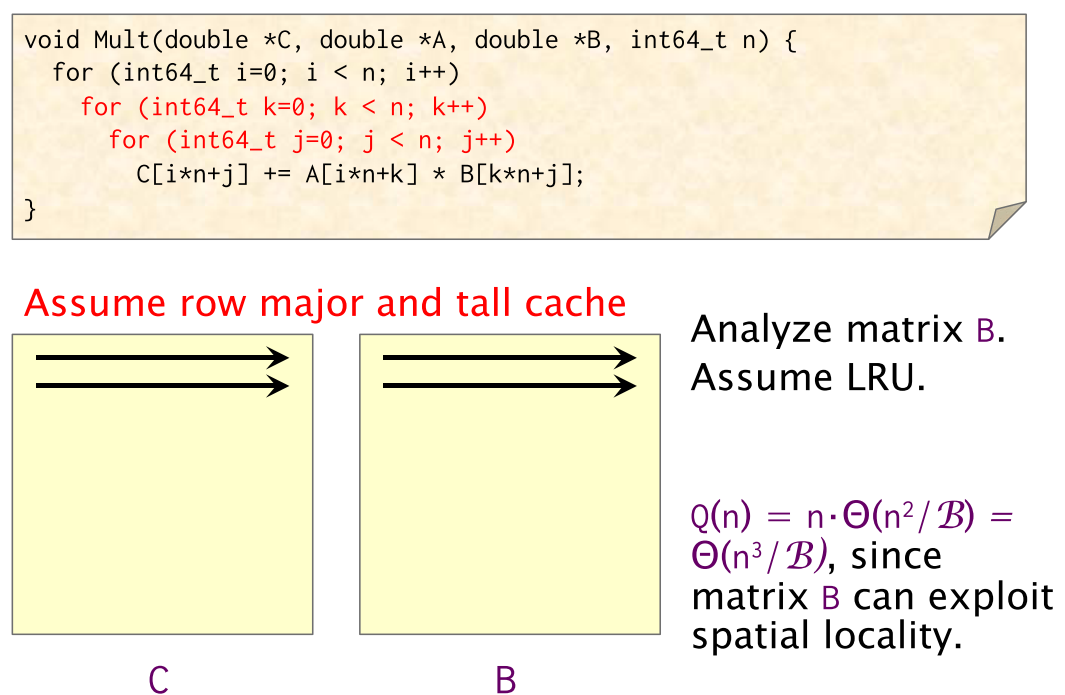
이하에서는 cache가 LRU replacement policy를 적용한다고 가정하고, matmul에서 B의 memory access pattern을 cache 관점에서 살펴본다.
Analysis of Cache Misses
Case 1:
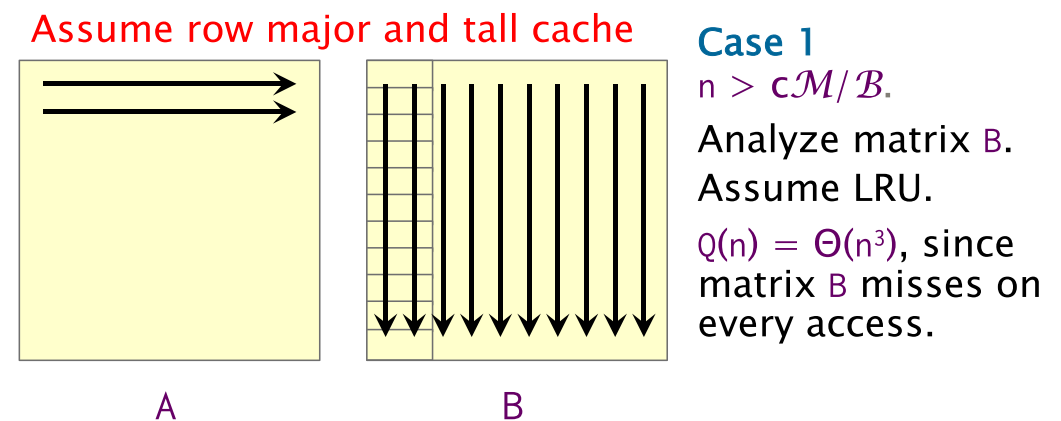
위 그림과 같이 matmul에서 A는 access하는 matrix의 address가 consecutive한 반면, B는 row address가 계속해서 바뀌기 때문에 B에서 access하고자하는 data가 cache에 없다면, cache eviction이 지속적으로 발생할 것이다. 이를 정량적으로 분석한 식이 이다. Cache의 replacement policy를 LRU로 가정했기 때문에 B의 첫번째 column access에서 를 넘어가는 row에 access를 할때마다 B의 row data가 eviction 될 것이다. 이는 B의 모든 row를 access할때 적용되므로 cache miss complexity는 이 되는 것이다.
Case 2:
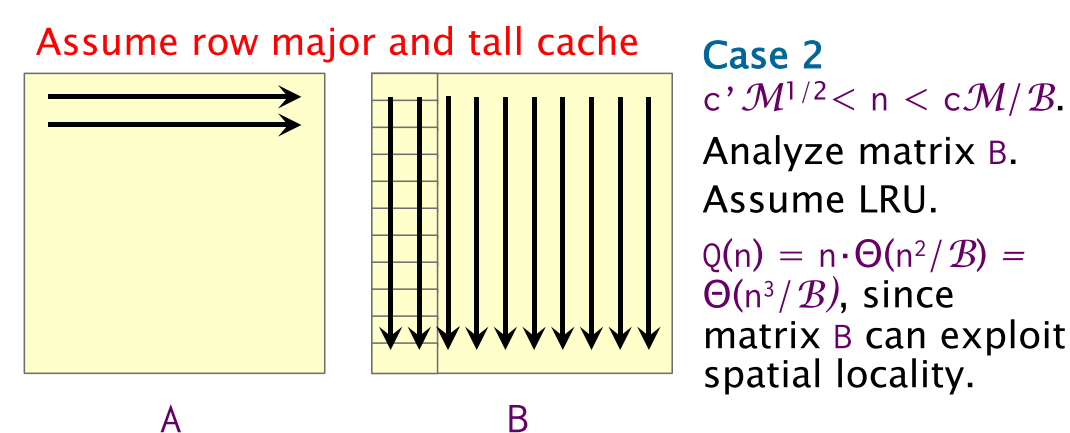
Case 1과 달리 matrix가 cache에 전부 다 load 될 수는 없지만, dimension이 line의 수보다 작은 경우다. Dimension이 line수보다 작기때문에 2nd column access에 spatial locality에 의한 data를 access 할 수 있다. 하지만 모든 matrix data가 cache 존재할 수 없기 때문에 A는 , B는 만큼의 cache miss가 발생한다.
Case 3:

Matrix의 사이즈가 cache보다 작아서 첫번째 cache miss를 제외하고 B의 2번째 column access부터 cache miss가 발생하지 않는다. 따라서 Case 3에 해당하는 cache miss complexity는 A에 대한 miss complexity 가 된다.
Swapping Inner Loop Order
위의 cache miss analysis에서 보는 것과 같이 matrix의 size에 따라 cache miss는 달라질 수 있다. 그렇다면 cache miss가 덜 발생하도록 matmul을 수행할 수 없을까? 당연히 있다. 가장 단순한 방법은 B matrix를 transpose하거나 B 에서 access 하는 element의 order를 바꾸는 방법이다. 컴파일러에서도 기본적으로 loop overhead를 줄이기 위해 loop interchange optimization을 알아서 수행해주고 있다. 얼마나 다행인가. Loop interchange에 대한 코드를 살펴보면 아래와 같다.