제약조건 만족 문제(constraint satisfaction problem)

주어진 제약조건을 만족하는 조합 해(combinatorial solution)를 찾는 문제

백트랙킹 탐색(backtracking search)

• 깊이 우선 탐색을 하는 것처럼 변수에 허용되는 값을 하나씩 대입
• 모든 가능한 값을 대입해서 만족하는 것이 없으면 이전 단게로 돌아가서 이전 단계의 변수에 다른 값을 대입

제약조건 전파(constraint propagation)

인접 변수 간의 제약 조건에 따라 각 변수에 허용될 수 없는 값들을 제거하는 방식

최적화(optimization)

여러 가지 허용되는 값들 중에서 주어진 기준을 가장 잘 만족하는 것을 선택하는 것

• 목적함수(objective function)
  • 최소 또는 최대가 되도록 만들려는 함수
• 조합 최적화
  • 유전 알고리즘
• 함수 최적화
  • 최대 경사법

조합 최적화(combinatorial optimization)

TSP 와 같이 주어진 항목들의 조합으로 해가 표현되는 최적화 문제
- TSP의 목적함수 : 경로의 길이

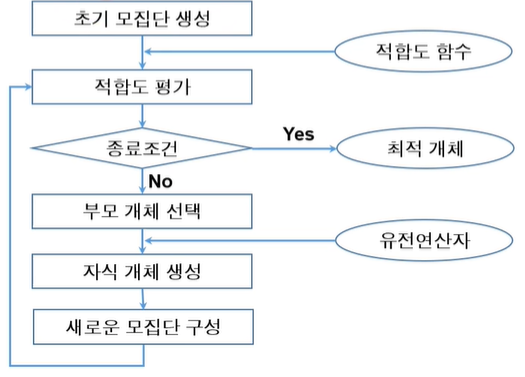
유전 알고리즘(genetic alogorithm, GA)

생물의 진화를 모방한 집단 기반의 확률적 탐색 기법

• 대표적인 진화 연산의 하나
• 생물 진화와 문제 해결
  • 개체 == 후보 해
  • 환경 == 문제
  • 적합도 == 해의 품질
    

• 후보해 표현 : 염색체 표현
• 모집단(population) : 동시에 존재하는 염색체들의 집합
• 적합도 함수(fitness function)
  • 후보해가 문제의 해로서 적합한 정도를 평가하는 함수
• 부모 개채 선택(selection)
  • 높은 적합도의 개체가 새로운 개체를 생성할 확률이 높도록 함
  • 적합도에 비례하는 선택확률
• 유전 연산자(genetic operator) : 새로운 개체 생성
  • 교차(crossover) 연산자
  • 돌연변이(mutation) 연산자
• 세대(generation) 교체
  • 엘리트주의(elitism) : 우수한 개체를 다음 세대에 유지

메타 휴리스틱(meta heuristics)

최적해는 아니지만 우수한 해를 빠르게 찾기 위한 휴리스틱적인 문제해결 전략

함수 최적화(function optimization)

어떤 목적 함수가 있을 때, 이 함수를 최대로 하거나 최소로 하는 변수 값을 찾는 최적화 문제

제약조건 최적화

제약조건을 만족시키면서 목적함수를 최적화 시키는 변수값들을 찾는 문제

회귀(regression) 문제의 최적 함수

주어진 데이터를 가장 잘 근사하는 함수

• 최소 평군제곱법(least mean square method)
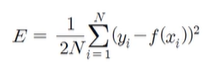
  • 오차 함수(error function) 또는 에너지 함수(energy function)를 최소로 하는 함수를 찾는 방법
    

경사 하강법(gradient descent method) = 최대 경사법

함수의 최소값 위치를 찾는 문제에서 오차 함수의 그레디언트(gradient) 반대 방향으로 조금씩 움직여 가며 최적의 파라미터를 찾으려는 방법

• 그레디언트 : 각 파라미터에 대해 편미분한 벡터
  
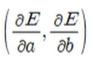
• 데이터의 입력과 출력을 이용하여 각 파라미터에 대한 그레디언트를 계산하여 파라미터를 반복적으로 조금씩 조정
  
• 국소해에 빠질 위험이 있다