문제

https://www.acmicpc.net/problem/1931

풀이

from sys import stdin

n = int(stdin.readline().rstrip())

time_table = []

for _ in range(n):
    begin_time, finish_time = map(int, stdin.readline().rstrip().split())
    time_table.append((begin_time, finish_time))

time_table = sorted(time_table, key=lambda a: a[0])
time_table = sorted(time_table, key=lambda a: a[1])

end_time = 0  # 마지막으로 끝난 회의 시간
conut = 0

for bt, ft in time_table:
    if bt >= end_time:
        conut += 1
        end_time = ft

print(conut)

문제에서 핵심문장은 다음과 같다.

"각 회의가 겹치지 않게 하면서 회의실을 사용할 수 있는 회의의 최대 개수를 찾아보자. "

여기서 최대 개수를 알기 위해서 어떤 것을 기준으로 정렬해야할지 고민해볼 필요가 있다.

1. 가장 짧은 작업 시간 순
2. 가장 긴 작업 시간 순
3. 가장 빨리 시작하는 회의 순
4. 가장 빨리 끝나는 회의 순

1,2,3번에 대한 반례는 쉽게 생각해볼 수 있을 것이다.
그렇다면 왜 4번일까?
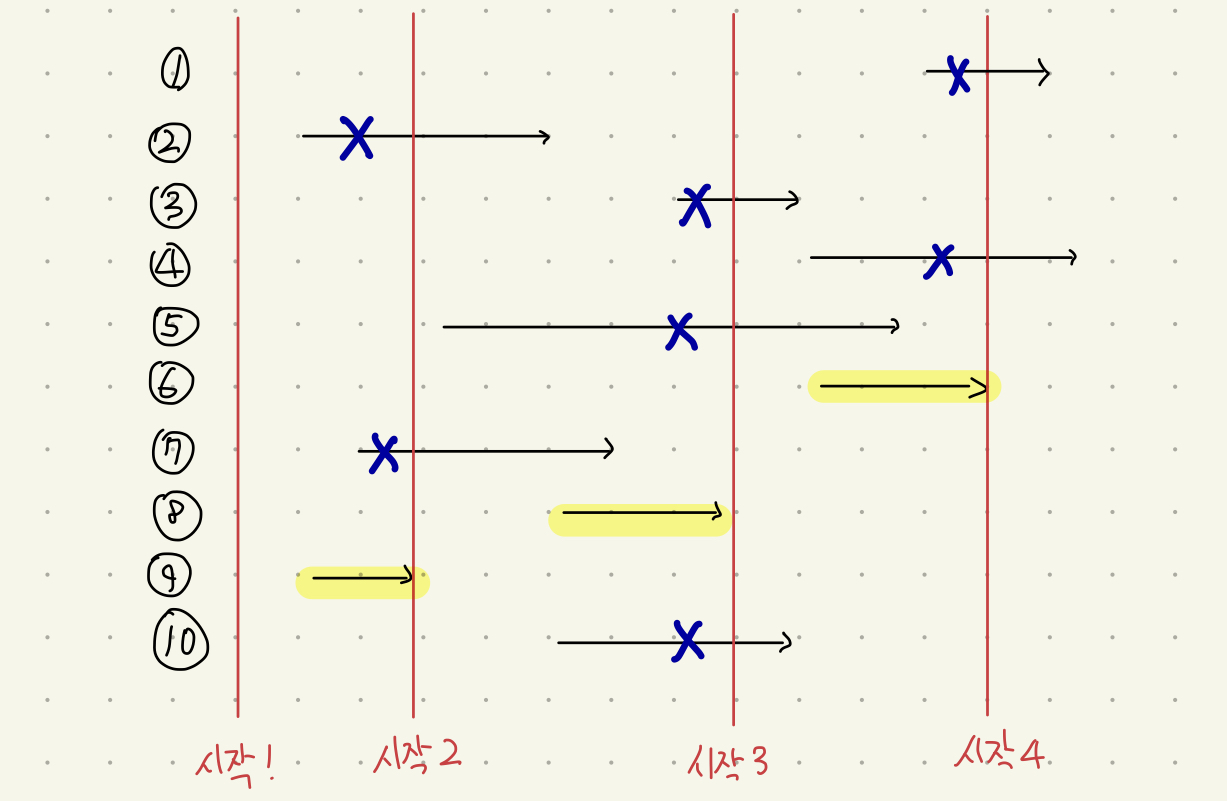
무작위로 10개의 회의를 만들었다.

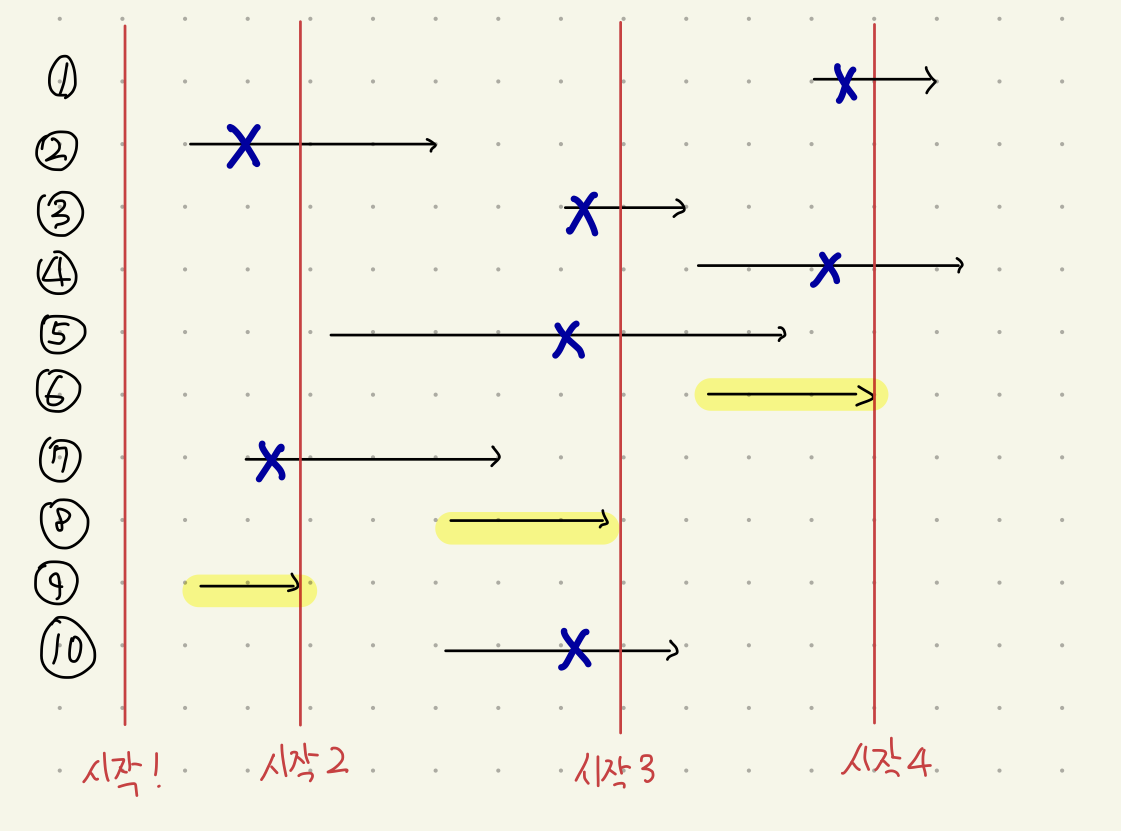
가장 빨리 회의가 끝난다는 뜻은 가장 빨리 다른 회의를 시작할 수 있다는 뜻이다.
가장 빨리 다른 회의가 시작 될 수록 가장 많은 회의가 열리게 되는 것(Greedy)이므로, 4번 기준으로 정렬하는 것이 맞다.

수학적 증명: https://gazelle-and-cs.tistory.com/59

정렬한 후 회의 중에 시작되는 회의를 제외하며 다음 회의를 찾아가면 답이 나온다.