프로그래머스 해시

Treeboy·2025년 3월 3일

acmicpc

목록 보기

2/2

의상 (level 2)

문제

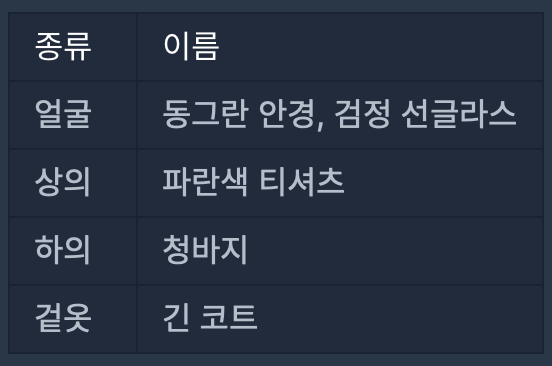
최소 1개 이상의 의상을 입는다고 할 때, 모든 의상의 조합을 구하는 문제이다. 한 종류에서는 하나의 의상만 입을 수 있다.

Solution

def solution(clothes):
    answer = 1
    
    # Construct hash out of the array
    myhash = {}
    for cloth, ctype in clothes:
        if ctype not in myhash.keys():
            myhash[ctype] = 0
        myhash[ctype] += 1
        
    # count combinations
    for key, item in myhash.items():
        answer *= item + 1
        
    answer -= 1
    return answer

해설

조합 문제이다.

\prod_{i=1}^{n}(a_i+1) - 1

이 공식만 알면 풀 수 있는데... (얼굴 종류 + 1) (상의 종류 + 1) ... (겉옷 종류 + 1) - 1

이 공식을 몰라서 1개를 고를때, 2개를 고를 때, 3개를 고를 때... 이렇게 나눠서 푸려고 하다가 결국 힌트를 봤다. 결국 챗지피티에게 이 공식이 어떻게 나오는지 유도해달라고 했다.

챗지피티 해설

이 식의 전개와 해석은 다항식의 곱셈 원리를 활용한 조합론적 전개와 같습니다.

예를 들어, $n$ 개의 의상 종류가 있고 각 종류 $i$ 마다 $a_i$ 개의 의상이 있다고 합시다. 그러면 각 종류에 대해 선택의 경우의 수는

a_i + 1 \quad (\text{실제 의상을 선택하는 } a_i \text{가지 경우 + 선택하지 않는 경우 } 1 \text{가지})

따라서 모든 종류에 대해 독립적인 선택의 경우의 수는

\prod_{i=1}^{n} (a_i+1)

가 됩니다.

이 곱을 전개하면 다음과 같이 표현할 수 있습니다:

\prod_{i=1}^{n} (a_i+1) = (a_1+1)(a_2+1)\cdots(a_n+1)

각 괄호에서 $a_i$ 또는 $1$ 을 선택하는 것과 동일합니다.
즉, 전개 결과의 각 항은 $i$ 번째 항에서 $a_i$ 를 선택했는지, 아니면 $1$ (즉, 선택하지 않음)을 선택했는지에 따라 결정됩니다.
구체적으로, 전개 결과는 모든 부분집합 $S \subseteq \{1, 2, \dots, n\}$ 에 대해

\prod_{i\in S} a_i

의 항들의 합으로 나타납니다.

만약 $S$ 가 공집합이면, 이 항은 $\prod_{i\in \emptyset} a_i = 1$ (아무것도 선택하지 않은 경우)입니다.
$S$ 가 단일 원소 집합, 예를 들어 $\{i\}$ 라면, 해당 항은 $a_i$ 가 되어 이는 오직 한 종류만 선택한 경우의 수를 의미합니다.
$S$ 가 두 원소 집합 $\{i,j\}$ 이면, 해당 항은 $a_i \times a_j$ 가 되어 두 종류를 모두 선택하는 경우의 수가 됩니다.
모든 종류 $\{1, 2, \dots, n\}$ 를 선택하면 항은 $\prod_{i=1}^{n} a_i$ 가 됩니다.