시계열 모델은 과거의 값이 미래의 움직임에 대한 예측 신호를 갖는 모델. 또한 횡단면 모델에서 사용되는 특성을 예측할 수 있는 모델. 모델의 목표는 시계열 데이터에서 패턴을 찾아내는 것이다.
시계열 모델에서는 시간이 명시적으로 나타나고, 특정 간격이나 lag에서의 변수를 포함하도록 동적 선형 모델을 구축한다. 주요 특성이 순차적 순서라는 점!
모델 특성상 그래서 자산 수익률, 변동성, 가격의 예측 등에 자주 사용된다.
- 특성 진단
- 정상성 진단 및 달성법
- 일변량 및 다변량 모델 도입
시계열의 패턴 분석은 근본적으로 개별 래그가 현재 값에 주는 영향을 분석하는 것.
횡단면 모델의 경우 x와 y에 대한 식이었지만, 시계열은 이전의 y값들이 x의 역할을 한다는 점.
백색 잡음: 시계열이 IID를 만족하면서 유한한 평균과 분산을 갖는 확률 변수 e_t의 순서열인 경우 이를 백색 잡음(white noise)라고 한다. 이 변수가 평균이 0이고 분산이 상수인 정규분포면 특히 가우시안 백색 잡음이라고 한다.
선형은, 시계열 식이 다음처럼 생기면 선형이다.
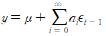
그리고 시계열 모델을 분석하는 이유는 각 a들의 행태를 이해하는 것이 된다.
시계열 모델에서 분해할 수 있는 요소들에는 추세(시간에 따라 증가, 감소하는 일정 수준), 계절성과 주기(일정한 주기로 반복되는 패턴), 잔차가 있다. 전자 2개는 체계적인 구성성분이며 뒤는 비체계적이다. 이들이 선형결합혹은 비선형 결합될 수 있다.
그리고 이를 분리하는 건 이미 파이썬에 있다.
(tsa는 time series analysis인듯)
import statsmodel.tsa.api as tsa
데이터~~
components= tsa.seasonal_decompose(df, model='additive')additive는 요소들이 합으로 모델을 만들지만 multiadditive은 요소들의 곱으로 생성된다고 한다.
그리고 이 compontnets안에
components.trend
components.seasonal
components.resid
로 각 요소들이 저장되어 있게 된다.
롤링 윈도우 통계량 : 특정 기간에 대해 요약 통계량을 나타내는 새로운 시계열을 만드는데, 이를 통해 안정성을 확인하고 잡음을 제거할 수 있다. 대표적인게 이동평균. 가중치는 전부 동일할 수도, 최근에 비중을 줄 수도 있다. 최근에 비중을 주는게 지수 평활화 모델. 복잡하거나 급작스럽지 않은 시계열에 사용하기 좋다.
autocorrelation: 자기 상관. 시계열에서 상관계수의 개념이다. 주어진 lag 값들 사이의 선형 관계 정도를 측정한다. 원래 식을 보면, lag T의 상관계수를 계산하기 위해서는 자연히 그 사이에 있는 lag기간에 의한 영향이 반영된다. 이런 영향을 제거하고 오로지 기간에 대해서만 하는 것이 PACF(partial autocorrelation function, 편자기 상관계수). AR(T-1)모델이기도 하다. ACF와 PACF간의 상관관계 구조를 한번에 보여주는 것이 correlogram(상관 도표)
stationary(정상적) 는 평균, 분산, 자기 상관이 기간에 독립이다. 즉, 추세나 계절 효과 없이 기술통계량이 상수임을 의미한다. strong stationary의 경우 any 부분집합의 결합 분포도 모멘트에 대해 독립이어야 한다. 즉, 평균, 분산, 왜도, 첨도 등도 불변이어야 한다. 근데 보통 여기까진 안하고 평균, 분산, autocorrelation까지만 보는 듯. 그러면 covariance stationry가 되는 듯 하다.
이때 기억할 점은, 시계열 모델의 경우 래그 출력값 간의 상관관계를 허용한다는 것이다. 선형회귀에서 결과와 데이터가 상관관계를 갖는 것을 허용하는 것과 같다.
대부분의 경우 stationraty를 위해 데이터를 변환해야 한다. log를 씌워 지수 증가를 선형으로 바꾸고 분산을 안정시키는 등의 작업을 포함한다. 시계열을 쪼개서 trend를 만드는 것으로 바꾸는 deflation도 변환의 한 종류다.
시계열이 장기 선형 추세로 회귀한다면 trend-stationary라고 한다. 선형회귀를 사용해 추세선을 최적화하고 잔차를 이용하는 것으로 가능하다.
하지만 보통 추세만 제거해서는 정상적이지 않다. 따라서 기간대 기간, 계절 대 계절 등으로 변환할 필요가 있다. d번 detrend하면 d차 공적분(integrated)되었다고 말한다.
로그 변환은 파이썬으로 간단하게 구현 가능하다.
(s==0).any()
s_log=np.log(s)시계열 데이터를 다룰 때 반드시 주의해야 되는 것이 단위근 문제이다.
단위근이란, 시계열의 자기회귀 형태 식에 대한 특성 방정식의 해 중에 1이 존재하는 것을 이야기한다. 즉,
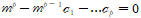
에서 근 중 하나가 1인 경우다.
이게 대체 왜 문제가 되는지는 예시를 보면 알 수 있다. 다음 블로그를 참고했다.
https://blog.naver.com/deniro33/222850888571
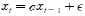
이식에서 unit root면 a=1이다.즉 랜덤 워크다.
근데 추정한 식에서 a의 절대값이 1보다 작을 때는 수렴하니 괜찮지만, 1보다 큰 경우를 생각해 보면, 임의로 정해지는 최초값에 따라 식이 발산하게 된다. 문제는 약간의 값의 차이가 시간에 따라 굉장히 커지게 되면서, 분산이 점점 커지게 된다는 것이다.
그래서 단위근 검정은 현 시계열 데이터에서 단위근이 있을 확률을 확인하는 테스트다. 가설이 기각되면, 추세가 없어 시간의 흐름에 따라 평균, 분산이 변하지 않는다고 생각할 수 있다. 그럼 이걸 어떻게 다루느냐.
원래 식이 위와 같았다고 하면, 이를 아래처럼 바꾸는 것이다. 이게 1차 differential(차분)가 된다.
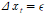
이 식의 경우, stationary하다.
검정은 흔히 확장 DF(ADF, Augmentetd Dickey-Fuller)테스트를 사용한다. 귀무가설이 기각되면 비정상적인 것이다. 모든 trend, 차분 래그에 대해 회귀식을 시행하고 통계량을 확인하는 검정이다.
식으로는 아래와 같다.
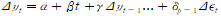
여기서 알파와 베타가 0이면 랜덤워크다. 베타만 0이면 drift가 있는 랜덤 워크다.
파이썬으로는
from statsmodel.tsa.stattools import acf, q_stat, adfuller
tsa.adfuller(시계열)[1] #여기에 p value가 들어있다.
p value가 충분히 작으면 단위근 비정상성을 기각할 수 있다. 반대로 말해 stationary하므로 시계열 데이터에 사용해도 된다는 뜻이다.
데이터에 대해 대강의 휴리스틱들이 있다.
- 0혹은 음에 가까운 래그-1 자기 상관계수 또는 일반적으로 작고 패턴이 없는 자기 상관계수
- 10개 래그 이상의 양의 상관계수 : 고차 차분 필요 가능성
- 래그-1 자기 상관계수 <-0.5 : 과대 차분 가능성
- 그 외 약간의 초과 혹은 미달은 AR이나 MA항으로 가능.
변환을 통해 ADF p value를 확인했으면, 이제 상관도표를 그려본다.
QQ그래프는 정규분포의 분위수와 비교한다. 그리고 ACF, PACF를 그려볼 수 있다.
제공된 코드를 저장해 놨다 나만의 유틸로 사용할 듯?
이렇게 정상성을 확보하고 나면, AR, MA, 혹은 ARMA 모델을 사용할 수 있다.
이와 달리 완전한 정상성은 아닌 데이터를 가지고도 만들 수 있는 ARIMA모델이라는 것이 있다. ARIMA모델은 데이터의 자기 상관관계를 묘사하는 것이 목표다. AR(AutoRegressive)(P래그) I(공적분)(d번 차분해서 단위근 비정상성) MA(Moving Average)(q 래그 교란항)이다.
그 기초가 되는 AR모델은 다음과 같다.
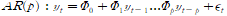
이 식의 특성 방정식은
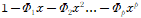
이며 절대값이 모두 1보다 작을 때 정상적이다.
이때 중요한 것은 사용할 p값을 결정하는 것이다. ACF를 이용하면 래그 k까지 유의하면 k까지의 값에서 유의한 상관관계를 보인다. PCAF에서도 유사한 관계를 보인다.
위처럼 lag간의 선형관계가 존재하고 이걸 포착하면, 에러 항은 백색잡음과 유사해져야 한다.
AR 모델을 사용해야 되는지는 Ljung-Box Q 통계량을 이용해 알 수 있다. 이 통계량이 유의하면 AR모델의 계수가 모두 0이라는 귀무가설이 기각되어, 적어도 하나는 유의하다. 카이제곱 분포를 따른다.
MA모델은 래그 대신에 노이즈 항들을 사용한다. 즉
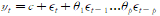
이다.
이때 중요한 포인트가, t시점의 노이즈 값은 관찰할 수가 없다. yt가 없으니 당연하다. 따라서 회귀 모델이 아니며, MLE(최대 우도 추정)을 이용해 추정한다. 즉 추정 후에 반복해서 재귀적으로 나머지를 추정한다. 다시 써 놓지만 이동평균 식인 것이다. 과거 추세에서 잡음을 제거하거나 추정하는 것이 아니라, 미래 값을 예측하는 것이 목표인 점을 기억해야 한다. 언제나 정상적인 백색 잡음의 가중 합이기 때문에 항상 정상적이다.
마찬가지로 q값은 ACF를 이용해 유의한 것까지를 보면 된다. AR과는 달리 PCAF는 유사한 관계를 보이지 않는다.
이제, AR(p) 모델을 반복 대입으로 MA(무한)으로 표현할 수가 있다. 이렇게 두 프로세스를 결합하해 양 쪽을 보완하고 간결한 형태를 만들어 오버피팅을 방지하기 위한 것이 ARIMA모델이다.
d차분을 사용해 비정상성을 제거하고 사용하는데, 예를 들어 ARIMA(p,1,q)는 아래처럼 생겼다.
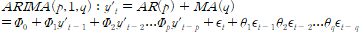
몇 차분을 사용할 건지는 지침이 있다.
차분이 없는건 원시 데이터가 정상적이라 가정한다. 상수항을 넣으면 0이 아닌 평균을 표현할 수 있다.
1차 차분은 원시 데이터에 일정한 추세가 있다고 가정한다. 따라서 상수항이 있어야 한다.
2차 차분은 원시 데이터가 시간 가변 추세를 갖는다는 것을 의미한다. 상수항은 없다.
ARIMA모델을 사용하면, AR과 MA의 p와 q가 상호작용하므로 ACF, PACF을 시작점으로만 사용할 수 있다. 역시 마찬가지로 지침이 있다.
- PACF가 소멸하는 점의 래그를 AR항의 수로 사용. 차분했을 때 PACF가 이후 급격히 소멸하거나 래그의 자기 상관이 양이면 AR항을 하나 추가
- ACF가 소멸하는 점을 MA항의 수로 사용. 차분했을 때 ACF가 이후 급격히 소멸하는게 보이거나 래그의 자기상관이 음이면 MA항 하나 추가.
- 모델이 AR및 MA를 포함하면 양측 항을 하나씩 줄인다. 그리고 모델 수렴을 위해 10번 이상 반복해도 하나씩 줄인다.
- AR 계수의 합이 거의 1이고, AR부분이 단위근이면 AR항을 하나 없애고 한 번 차분
- MA 계수의 합이 거의 1이고, MA 부분이 단위근이면 항을 하나 제거하고 차분 차수를 하나 줄임
- 그럼에도 장기 예측이 불안정하면 AR이나 MA가 단위근 가짐.
실코드를 보면 statsmodels.api에서 ARMA는 없어졌다. differential 안하고 ARIMA를 적용해도 되기도 하고, SARIMAX가 잘되어 있기 때문이라고 한다.
SARIMAX는 ARIMA에 계절성(S) 및 외부 변수(exog)를 더해준 모델이다. 여기에는 seasonal component인 PDQs도 같이 넣어준다. (s는 예를 들어 12개월 이면 12) P,Q는 pacf, acf에서 계절성 주기가 몇번 등장하는지이다.
이제 코드를 보자.
l3 = list(range(3))
l4 = list(range(4))
params = [t for t in product(l4, l4, l3, l3) if t[0] > 0 and t[1] > 0]
len(params)우선 파라미터를 생성했다.
왜 코드를 이런식으로 했나 모르겠지만 여하튼 총 81개다.
이거에 대해 이제 SARIMAX를 돌린다.
train_size = 120 # 10 years of training data
results = {}
test_set = industrial_production_log_diff.iloc[train_size:]
for p1, q1, p2, q2 in tqdm(params):
preds = test_set.copy().to_frame('y_true').assign(y_pred=np.nan)
aic, bic = [], []
if p1 == 0 and q1 == 0:
continue
convergence_error = stationarity_error = 0
y_pred = []
for i, T in enumerate(range(train_size, len(industrial_production_log_diff))):
train_set = industrial_production_log_diff.iloc[T-train_size:T]
try:
with warnings.catch_warnings():
warnings.filterwarnings("ignore")
model = tsa.SARIMAX(endog=train_set.values,
order=(p1, 0, q1),
seasonal_order=(p2, 0, q2, 12)).fit(disp=0)
except LinAlgError:
convergence_error += 1
except ValueError:
stationarity_error += 1
preds.iloc[i, 1] = model.forecast(steps=1)[0]
aic.append(model.aic)
bic.append(model.bic)
preds.dropna(inplace=True)
mse = mean_squared_error(preds.y_true, preds.y_pred)
results[(p1, q1, p2, q2)] = [np.sqrt(mse),
preds.y_true.sub(preds.y_pred).pow(2).std(),
np.mean(aic),
np.std(aic),
np.mean(bic),
np.std(bic),
convergence_error,
stationarity_error]우선, tqdm은 여러 iterate이 되는 것을 넣어가면서 값을 실험해 볼때, 얼마나 진행됐는지를 보여주는 툴이다. 그래서 사용.
매 iteration마다 바가 올라간다.
각 iteration마다, predict를 실행해야 한다. 또한, aic, bic도 측정해야 한다. 그래서 해당 저장 배열을 만든다.
이후 iteration을 해 가면서 값을 예측해보게 된다. model.forecast를 통해 예측 값을 넣게 되고, aic, bic를 기록한다.
aic는 파라미터 수에 대한 패널티가 있으며, BIC는 변수의 수에 대한 패널티도 추가되어 있다. 우선순위에 따라 둘을 다르게 사용하면 된다. 이후, results에 해당 파라미터 값에 따른 mse, aic와 bic 통계치들을 저장해 두게 된다. 이후,
sarimax_results.nsmallest(5, columns='RMSE')
를 사용하면 RMSE가 가장 작은 5개의 조합을 골라준다.
BIC도 같이 보려면
sarimax_results[(sarimax_results.RMSE < sarimax_results.RMSE.quantile(.05)) &
(sarimax_results.BIC < sarimax_results.BIC.quantile(.1))].sort_values('RMSE')이 코드로 RMSE와 BIC를 같이 챙길 수 있다.
이렇게 최적 파라미터를 선택하고 나면
model=tsa.SARIMAX(~)
print(model.summary())로 결과를 볼 수 있다.
p value, 그리고 기타 통계치를 통해 유의성 또한 확인 가능하다.
위는 분산이 iid를 따른다고 가정하게 되는데, 실제의 경우 변동성이 변할 때가 생기게 된다. 일시적으로 변동성이 클러스터링 되는 경우가 대표적이다. 이런 문제를 다루기 위해 변동성 모델이 나왔다.
heteroskedasticity가 분산 변화를 나타내는 용어. ARCH 모델은 분산을 오차항의 분산을 이전 오차들의 함수로 표현해 준다. (즉 오차 변수가 AR(p)를 따른다.)
GARCH(generalized ARCH)는 이걸 ARMA모델까지 확장해 준 것이다.
ARCH(p) 모델의 식은 다음과 같다.
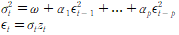
여기서 z는 교란항이다.
강점은, 변동성을 생성하고 수익률에 대해 양의 초과 첨도(kurtosis)(조금더 뾰족), 그리고 fat tail을 가정한다는 것. 약점은 양과 음의 변동성 충격을 동일하게 묘사한다는 것(실제로는 다르게 반응), 그리고 기계적인 묘사로 통찰력을 제공하지 못한다는 단점이 있다.
ARCH모델을 만들고 나면 잔차를 표준화 했을 때 백색 잡음과 비슷해진다. 따라서 룽박스 Q테스트를 적용할 수 있다.
GARCH(1,1)는 사실 ARCH(무한)과 동치다. 그러면서도 매우 적은 파라미터로 나타낼 수 있기 때문에 굉장히 효율적인 것이다. 물론 여기서도 더 변형된 모델들이 있다. HAR는 여러 빈도에 대해 예상 평균을 모델링하는 옵션을 제공한다. EGARCH는 양과 음의 수익률의 비대칭 효과를 고려한다. GARCH는 HAR의 보완이다.
GARCH(p,q)모델은 다음처럼 생겼다.
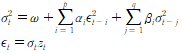
마찬가지로 fat tail이다. 긜고 여전히 양과 음의 충격을 동일하게 처리하는 단점이 있다.
이 모델은 다음 단계로 사용한다.
1. 우선 ARMA모델을 만들어서, ACF과 PACF를 적용해 모델을 만든다.
2. ARCH, GARCH 효과가 있는지 확인하기 위해 잔차를 확인해 본다. 즉, 잔차 제곱의 시계열에 대해 ACF와 PACF를 적용한다.
3. 시계열에서 유의한 상관관계가 나타나면 변동성 모델을 설정해 평균과 변동성 식을 동시에 추정한다.
4. 모델을 보고 필요시 개선한다.
역시 파이썬에서는 구현되어 있다.
from arch import arch_model
from arch.univariate import ConstantMean, GARCH, Normal
model=arch_model(y=train_set, p=~, q=~).fit(disp='off')
forecast=model.forecast(horizon=1)
am=ConstantMean(~)
am.volatility=GARCH(best_p,0,best_q)
am.distribution = Normal()
best_model=am.fit(update_freq=5)
print(best_model.summary)
ARMA, ARMAX(외생변수가 추가 됐다고 해도)와 같은 일변량 시계열 모델과 달리, 다변량 시계열 모델은 다른 시계열의 래그값을 추가할 수 있다.
여기에 사용하는 것들은 충격-반응 함수(어떤 변수가 다른 변수의 갑작스러운 변화에 어떻게 대응)
그레인저 인과성(한 변수가 다른 변수를 예측하는데 어떻게 유용한지)
VAR(vector AR) 모델:
모든 k시계열에 각각 p개의 래그 값을 포함하는 k방정식 체계 생성. 예를 들어 k=2인 VAR(1):
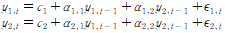
는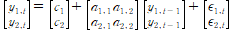
이기도 하다. 교차 계수들을 통해 시계열 간의 상호작용에 대한 통찰력을 얻을 수 있다.
VAR(p) 모델은 정상성을 필요로 한다. 따라서 정상성을 확인하는 일련의 과정(1. 시계열 조사, DF테스트 2. 오차의 정규분포 확인)을 실행해야 한다. 단위근을 다룰 때는 차분을 이용한다. 차분외에는 따로 도구가 없어 벡터 오차 수정 모델을 이용해야 한다.
래그 차수는 마찬가지로 ACF, PACF에서 출발하지만 래그 차수가 모든 시계열에 적용되어야 한다.
VAR의 파이썬 코드는 아래와 같다. VARMAX를 사용한다.
from statsmodels.tsa.api import VARMAX
model = VARMAX(df, order=(1,1),trend='c').fit(maxiter=1000)
print(model.summary)
model.plot_diagnostics(variable=0, figsize=(14,8), lags=24)
plt.gcf().suptitle('Industrial Production - Diagnostics', fontsize=14)
plt.tight_layout()
plt.subplots_adjust(top=.93);trend=c는 추세가 상수라는 것을 의미한다.
아래 부분은 백색 잡음 가정을 만족하는지의 그래프를 보여준다. 분산의 분포를 통한 상수 여부와, QQ그래프를 통한 fat tail 여부등을 볼 수 있다. 또한 예측을 생성해 비교해 볼 수도 있다.
