*본 글을 MIT의 Gilbert Strang 교수님의 선형대수학 강의를 정리한 글입니다. 유튜브에 올라와 있습니다.
선형 대수학은 이런식으로 Ax=b에 대해 해를 내는 과목이다. 다만 첫째, 행렬과 벡터를 이용한 연산이라는 것이고, 둘째로 나중에는 해가 없는 경우에도 최적해를 낼 것이다.
행렬 연산 기본
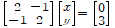
예를 들어 이런 행렬연산이 있다고 하자.
이 문제를 보는 시점에는 두 가지 방법이 있다. 첫째는, 2x-y=0 , -x+2y=3 라는 두 직선의 교점을 찾는 row식 해석, 두 번째는 [2,1]' 과 [-1,2]'라는 두 벡터의 선형 결합으로 [0,3]'를 만들어내는 column picture 두 가지이다.
3*3 짜리에 대해서는 똑같은 방식으로 row는 3개의 평면이 만나는 교점, column은 3개의 벡터의 선형결합으로 볼 수 있을 것이다.
위와 같은 벡터 X 행렬 연산은 다음과 같다.
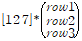
1row1+2row2+7*row3 가 나오게 된다.
이걸 행렬 곱 행렬로도 확장할 수 있다. 이 경우 얻은 결과물이 각 row가 된다.
이를 비롯해, 행렬끼리의 곱은 4가지의 방식으로 해석할 수 있다.
A*B=C일 때
1. 원래 규칙
2. C의 column들이 A의 column들의 선형 결합
3. C의 row가 B의 row들의 선형 결합
4. C의 모든 원소들이, A의 row와 B의 col를 곱해 생기는 matrix의 총합
이라는 4개 해석 방법이 생긴다.
이를 조금 더 확장해, 행렬을 블록으로 쪼개 곱을 하는 것 또한 가능하다.
역행렬이 존재하면, AA^(-1)=A^(-1)A=I. 이때 A를 singular matrix라고 한다. Square때만 이 교환이 성립하며, Square가 아니면 left inverse, right inverse가 있을 수 있다. 후술 하겠지만, Ax=0의 해가 있는 경우 역행렬이 존재하지 않는다.
행 혹은 열끼리의 교환은 permutaion이라고 한다. row 교환은 대상 행렬의 왼쪽, col교환은 대상 행렬의 오른쪽에 있게 된다. 예를 들어
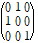
는 대상 행렬의 왼쪽에 있으면 row를 교환해 주지만, 오른쪽에 있으면 col를 교환해 준다.
그 외 기타 역행렬 관련 연산
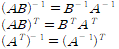
더불어, 행렬을 이용하는 것은. linear transformation에 해당한다. 모든 선형 변환에는 그에 해당되는 matrix가 있다. matrix를 이용한 변환이 특히 좋은 건, 사실 이런 변환에 해당하는 matrix가 없다면, 모든 점을 일일히 따로 계산했어야 됐을 것이기 때문이다. 하지만 그럴 필요 없이 행렬을 이용해 한번에 변환시킬 수 있다. matrix의 basis가 coordinate에 해당한다.
Complex vector, matrix
보통 실수 벡터의 길이는 다음처럼 계산한다. x'x.
complex의 경우는 이렇게 계산하면 안된다. xbar'x로 계산해야 된다. 즉 conjugate를 이용하며, 이때 xbar'를 x^H(hermitian) 이라고 표기한다. 행렬을 이용해 퓨리에 변환을 할 때 이 hermitian 필요.
Elimination
elimination. 당시 기준, 모든 프로그래밍에서 사용했던 방법이라고 한다. 아마 지금도 마찬가지일 것 같지만.
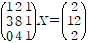
이 해를 구한다고 할 때, elimination과정은 다음과 같다.
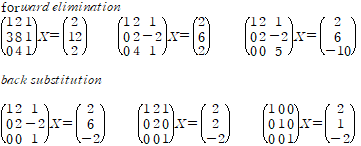
여기서 elimination의 끝 단계의 행렬을 보통 U(upper triangle)로 표기한다. 그리고 이때 대각선의 값들을 pivot이라고 한다.
A|I -> I|X 로 elimination을 했다면 X가 A의 역행렬이다. 이걸 gauss jordan elimination이라고 한다.
elimination과정에서 깔끔하게 pivot이 나오는 경우도 있겠지만, 0이 중간에 있는 경우도 당연히 생긴다. 이 경우 필요한 건 row exchange. 이번 case에서는 없었다. row exchange는 고려하지 않은 상태에서, elimination 과정을 행렬 연산으로 표현할 수 있다.
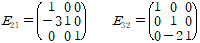
이렇게 정의 했을 때,
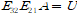
처럼 표현할 수 있다. 2행과 1행에 대한 것이 A바로 옆에 먼저 등장한다. 이런식으로 행렬을 만드는 것의 장점은, 역행렬을 이용해 역으로 되돌리는 작업이 단순하다는 것이다. 대각선을 제외한 부분들의 값의 부호를 바꿔주면 된다.
이를 이용해 gauss jordan을 증명할 수 있다.
여러 E들이 있어서, 이를 곱한게 E일 때 EA=I 라면, 이 E가 A의 역행렬이다. 이 E는 보면 lower triangle(permutation이 없다면) 를 취하고 있기 때문에, 역행렬도 lower triangle 꼴을 얻게 된다.
그래서 이를 종합해, A=LU 형태로 표현한다. 참고로 여러 행렬곱에 역행렬을 씌우므로 순서는 뒤집힌다. 과정을 생각해 보면 당연한 것.
여기서 이 방법의 최고 장점이 생긴다. 역행렬들을 곱한 결과물을 봤을 때, 'multiplier들이 L에 직접적으로 들어가게 된다' 즉, 이전 역행렬에서 나타난 값이 정확히 그 위치 그대로 들어가게 된다는 것. 이러면 연산량이 극도로 줄어들게 된다!
생각해 보면 당연하게, Elimination이 완료된 후의 row들은 서로 pivot을 가진 독립 행들이 된다. 따라서, 독립행들로 기존의 행을 만들 방법은 유일하고, 서로 independent해야 정상.
행 교환이 이제 머리가 좀 아파지겠지만... 아마 그래서 문제를 설계할 때 데이터셋을 행에, feature를 column에 두는게 아닌가 생각한다. 데이터셋은 independent한 경우가 대부분이므로, 순서를 바꿔 놓은 다음에 진행을 해도 굳이 그걸 원래대로 돌릴 필요가 없지 않을까...
Permutaion이 있는 경우는 PA=LU처럼 표현한다. P가 있다고 해서 그렇게 복잡해지지는 않는데, P는 P'가 P의 역행렬이라는 특성을 갖기 때문이다.
Vector Space
예를 들어 R2는 모든 2차원 real vector들이 모여 있는 vector space. 단 하나의 점이라도 빠져 있다면 이건 vector space라고 볼 수 없다.
그 중에서도 subspace라는 것이 있다.
subspace의 조건은, vector 끼리의 선형 결합, 그리고 multiplication에 대해 closed되어 있어야 된다는 조건을 갖는다.
R2를 처음에 예로 들어서 헷갈릴 수 있지만, 꼭 전체 공간을 다 포함해야 되는 것은 아니다. 예를 들어, R3에서 평면은 여전히 subspace가 될 수 있다. 단, 조건에도 있드시 multiplication에 closed되려면, '반드시' 원점을 포함해야 된다. 이는 모든 subspace에 해당되는 것으로, 반드시 원점을 포함해야 subspace가 될 수 있다. 0벡터만 들어 있는 것이 가장 작은 subspace가 된다.
따라서 subspace 두개의 단순 합집합은 subspace가 아니다. 두 평면이 교차할 때, 두 평면위의 벡터를 합했을 때 합집합 안에 있지 않는다. 반면 교집합은 subspace이다.
어떤 행렬이 있을 때, 예를 들어

라는 행렬이 있다고 하자. 이 경우 이 행렬의 column space는 R4의 subspace일 것이며, row space 는 R3의 subspace일 것이다. 물론 column space를 보면 알 수 있지만 평면이다.
여기서 중요한 포인트가 나온다.
Ax=b의 해가 존재하는가? 는, 달리 말해 b가 A의 column space안에 있는가? 와 동일한 질문이 된다는 것이다. (유일성은 다른 문제다.)
또한, Ax=0이 되는 벡터들을 모은 것이 nullspace이다. 적어도 원점 벡터가 포함되어 있다. (null space의 선형 결합을 보면 subspace라는 것을 알 수 있다.)(null space와 달리 Ax=b의 해들은 subspace가 아니다. (자명))
NullSpace에 0벡터가 아닌 벡터들이 있다면, 해는 무한해진다.
Vector space라고 되어 있지만, 사실 행렬들을 이용해 vector space를 만들 수도 있다. 이에 해당하는 subspace를 몇개 써보면, all upper triangle matrix, all diagonal matrix, all symmetric matrix등이 이에 해당된다. 여기에 대해서도 똑같이 dimension을 정의할 수 있고, basis 또한 찾을 수 있다. symmetric의 경우 6개다. 이런 경우 새로운 연산이 정의되는데, A+B는 둘의 합집합이 아니고, A vector space에 있는 것 하나와 B subspace에 있는 것 하나를 합친 것 으로 정의 한다.
Ax=b
Ax=b를 풀기에 앞서, Ax=0부터 풀어봐야 한다. 미방을 풀 때와 같게, general sol에 해당된다.
Ax=0의 경우, 이를 해결하는 알고리즘이 있다.

이런 행렬이 있었다고 하자. 여기에 elimination을 실행하고 나면 아래처럼 된다. 보통 처음 행렬을 A, elimination을 마친 행렬을 U라고 한다. A에 대한 NullSpace와 U에 대한 NullSpace가 같다는 점이 특기할 부분이다.

Ax=0
=> EAx=0
= Ux=0
1행과 2행에 pivot이 하나씩 있는것을 확인할 수 있다. 이렇게 pivot이 있는 col외에, pivot이 없는 col도 있다. pivot이 있으면 pivot col, 없으면 free col라고 한다. 또한, pivot의 수를 rank라고 부른다.
null space는, free col에 하나씩 1을 넣고 나머지는 0을 넣는 과정을 통해 찾게 된다. 위 예제의 경우 구체적으로 2번, 4번 값에 한번씩 1을 넣는다. 그러면 null space는 [-2,1,0,0], [2,0,-2,1] 이 벡터들의 선형결합으로 이루어진 subspace가 된다.
위 예시에서 볼 수 있듯, nullspace의 차원은 free variable의 수와 일치한다. 즉, 'row 차원수' - rank (즉 m*n 행렬의 경우 n-r) 차원이 된다.
위의 U를 Reduced Row Echelon Form 에서 따와 R로 표기하기도 한다.
역이 마찬가지로 계산을 줄일 수 있는 팁이 존재한다. R에서 pivot들을 전부 1로 맞춰도 null space에는 변화가 없기 때문에, 이를 1로 맞춰주고, back elimination을 해 준뒤 column 및 row들을 적절히 교환하면, 아래와 같은 형태를 만들어 줄 수 있다.
(둘은 같은 행렬인데 이렇게 표현)
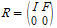
이러면 Nullspace를 매우 빠르게 구할 수 있다. [-F I]' 를 대입해 보면, 그 해가 0이 되고, 따라서 그 column들로 이루어진 subspace가 null space가 되는것을 알 수 있다!
Ax=b(해가 있는 경우) 도 이와 크게 다르지 않다. 단 차이점은, 이번에는 free variable에 모두 0을 넣어준 다는 것이다. 모두 0을 넣어준 값에다가, null space를 구할 때 구한 벡터들의 상수배를 더해주면 그게 전체 solution이 된다.
Ax=b는 subspace가 절대로 될 수 없는데, 그 이유는 원점이 들어가지 않기 때문에 바로 기각되어 버린다. 단, 원점에서 평행이동을 시킨 subspace는 맞다.
general case에 대해 정리하면 아래와 같다. A가 m*n짜리 행렬이며 rank 가 r일때
1. r<=n, r<=m (in all case)
2. r가 full column rank(r=n, n<m)일 때, free variable가 없으므로 null space는 원점 하나 뿐이며, 따라서 해는 1개거나 없다.
3. r가 full row rank(r=m, m<n)일 때, free variable가 반드시 있으므로 모든 b에 대해 해가 무한개 존재 한다.
4. r=m=n : 역행렬이 존재한다. 따라서 단일 해만 존재한다.
즉, rank가 해가 어떤지를 바로 알려준다는 것.
Vector independence, basis
여러 독립된 벡터들이 있을 때, 이를 span하면 vector space가 된다.
basis는 벡터들이 1. 서로 독립적이며 2. span 시 space가 되면 space의 basis라고 한다.
독립의 정의는, 모두 0의 계수를 곱하는 경우를 제외하고, 어떠한 선형결합으로도 0 벡터를 만들 수 없을때 이를 독립이라고 한다. 예를 들어 [1,2]' 와 [0,0]이 있다면 (1,0) 으로 0벡터를 만들어 낼 수 있기 때문에 독립이 아니게 된다.
column이 independent할 조건을 해 보면, rank 가 full column rank인 경우 independent하다는 것을 알 수 있다.
basis는 non unique하다. 하지만 동일 공간에 대한 basis의 개수는 언제나 일정한데, 이를 dimension이라고 한다. 이에 따라, 역행렬이 존재하는 square 행렬의 column space는 col가 모두 basis가 된다. 역행렬이 존재하므로 rank 는 n이고, 따라서 column space는 Rn이 되므로 basis는 n개이며, rank가 n이므로 모두 독립이기 때문이다.
null space에 대해서도 이것이 성립하게 된다.
Strang 교수님이 수업 내내 강조하신 4개의 subspace가 있다.
column space(<=Rm), row space(<=Rn), null space, null space of A'이다. 그림으로 보면 아래와 같다.
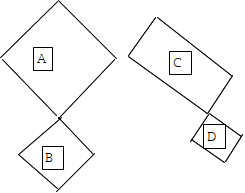
그림이 엉망이긴한데 대충 A는 row space, B는 null space, C는 column space, D는 null space of A' 로 보면 된다.
표로 특징을 보면
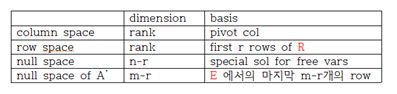
이다.
마지막 것은 A'y=0 <=> y'A=0 인걸 볼 수 있다.
중요한 점이 있는데, column space of A는 column space of R가 아니지만 row space는 A와 R이 같다는 것이다. 선형 연산을 row에 대해 하기 때문!
Graphs
선대를 실제로 사용하게 되는 대표적인 방법이 그래프를 이용하는 것이다.
예를 들어, 회로에서 node들이 있고, node 사이에 흐르는 전류를 다음처럼 표시할 수 있다.

이런 행렬이 있다면, 각 row들을 하나의 edge가 될 것이며, 예를 들어 row 1은 node1번에서 전류가 1나가고 node2로 전류가 1 들어온다고 해석할 수 있을 것이다.
이 상황에 대해 물리적으로 해석하면 다음과 같다. 이 행렬을 이용해 Ax=b를 찾는다면, 이때 x는 node들의 포텐셜이라고 볼 수 있다. 따라서 Ax는 edge를 따른 potential difference 일 것이다. 포텐셜 difference는 독립적이지 않고, 모두 더했을 때 0이 되어야 하므로 자유도는 n-1일 것이다.
row 가 edge라고 했으므로 특이하게도 null space of A' 에 특별한 의미가 생긴다. 이 subspace의 dimension은 2다. 즉, 키리히호프의 전류 법칙을 확인하게 될 루프의 수가 2개라는 것을 의미하기도 한다. 왜냐하면 edge의 조합으로 삼각형이 만들어지기 때문이다.
이 문제에서 rank는 3이다. 이 의미는, 3 점에서의 포텐셜을 알면 나머지는 자동으로 따라온다는 의미로 볼 수 있다는 것이다.
이 관계를 통해 굉장히 재미있는 사실을 알 수 있다.
row는 edge의 수를 의미했다. 그리고 null space of A'는 루프의 숫자였다. column의 수는 node의 수 였다. 그리고 null space의 diminsion은 1이었다.
따라서, r=col dim-null space dim = row dim-null space of a' dim
따라서 node-1=edge-루프. 루프의 수=edge의 수-(node의 수-1)이라는 굉장히 유명한 공식을 여기서도 얻을 수 있다.
Projection
Ax=b에 대해, '최적해'를 구하는 방법은 projection이다. 이때 A'A가 매우 중요하므로 먼저 살펴본다.
A'A는 다음의 특징을 갖는다.
- square이다.
- symmetric이다.
- A'A의 rank가 A의 rank와 같다.
- 따라서 A'A가 invertible하려면, A의 column이 독립적일 때만 invert 가능하다.(증명 생략)
이제 Ax=b로 돌아가서, 만일 이 문제에 대한 직접해가 존재하지 않는다면, 그나마 최적의 해를 내기 위해서는 b벡터를 A에 projection해야 한다.
e=b-p(p가 projection)일 때,
1. p=xa
2. a 수직 e <=> a 수직(b-xa) <=> a'(b-xa)=0
x=a'b/a'a, p=ax므로 p=a*a'b/a'a 라는 결과를 얻게 된다.(벡터) 벡터에만 해당되는 것이 아니라, 행렬에 대해서도 동일한 결과.
다시 정리하면
여기서 p가 갖는 중요한 특징이 2가지 있다.
1. P'=P
2. P^2=P 다.
따라서, A'Ax=A'b (x는 xhat이다.)를 푸는 것이 된다.
x(hat)=(A'A)^(-1)A'b 가 최적해가 된다. 딥러닝에서 볼 수 있는 공식이기도 하다. 연산량이 너무 많아 사용할 수 없다는 그 공식...
더불어, P(projection matrix)는 따라서 A(A'A)^(-1)A' 이 된다. 왜 역행렬이 안 풀려 있냐면 A가 square가 아닐 때도 사용되기 때문이다.
Projection matrix를 이론적으로 보면, b가 column space에 있을 때는 b가 그대로이며, 수직일 때는 0으로 project된다. 실제로 대입해보면 그게 맞다는 것을 알 수 있다.
실제 예를 한번 보면,
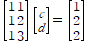
를 푼다고 생각해 보자. 이 문제는(1,1),(2,2),(3,2)를 지나는 직선의 최적해를 찾는 것과 같다. 즉 c는 상수이고, d가 기울기가 된다.
공식을 적용하면,
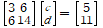
이 되며 d=1/2, c=2/3이 된다.
이 해는 미방으로 풀었을 때 LSE 방식으로 구한 것과 동일한 해를 갖는다. 즉 loss의 제곱값을 c와 d에 대해 미분한 값을 0으로 만드는 값이자, 에러의 합을 0으로 만드는 값이다.
Orthogonal Vector
4개의 주요 subspace의 또 하나의 특징은, row space/null space, column space/null space of A'는 서로 / 앞뒤 끼리 수직하다는(orthogonal)하다는 것이다.
벡터가 orthogonal 하다는 것은 둘이 수직이라는 것이다. 즉, 내적값이 0이라는 것이다. (참고로 0벡터는 몯느 벡터와 수직)
subspace끼리 orthogonal하다는 것은 이의 확장이다. 하나의 subspace에 있는 모든 벡터가, 다른 subspace에 있는 모든 벡터와 언제나 수직이라는 것을 의미한다. xy평면과 xz평면은 따라서 orthogonal 관계가 아니다. x축을 따른 공통 부분이 있기 때문.
orthogonal가 될 조건은 두 가지다.
1. intersection은 원점 밖에 없다.
2. Rn에 속하는 두 subspace의 dimension 합이 n이다.
orthogonal vector가 중요한 이유는 이것이 orthogonal basis를 만드는데 사용되기 때문. orthogonal basis는 다음 처럼 정의 된다.
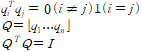
Q는 matrix with orthogonal columns이다. (약속으로, orthogonal matrix는 square때만 그 명칭을 사용한다.)
Orthogonal matrix는 굉장히 중요한 matrix의 subset이다. 이유는 역행렬을 계산할 필요가 없기 때문인데, 즉 P를 계산할 때 Q'Q=I가 되어, P=QQ'이 되어 버리는 것이다. 만약 square라면? P=I가 되어 버린다.(n개의 independent column을 가지므로 정상이다.)
P가 저렇게 된다는 것은 결국, xhat=Q'b 라는 간단한 식으로 바로 최적해를 낼 수 있다는 굉장한 장점으로 오게 된다.
퓨리에 시리즈로의 변환도 이와 동일한 방식이다. term들이 수직이기 때문에, 각 term에 곱해주면, 같은 것들만 남고 나머지는 없어지게 된다.
하지만 당연히 일반적인 matrix는 orthogonal basis를 갖지 않는다. 일반 independent basis를 가진 matrix를 orthogonal basis를 갖도록 하는 것이 gram-schmidt방법이다.
Gram-Schmidt
위 내용의 연장이지만 따로 분리.
a와 b가 있을 때, e=b-p라고 하면, 이 때 e가 a와 수직이게 된다. 그렇다면 이 e를 B, 기존의 a를 A라 하면, A와 B는 서로 orthogonal 한 벡터가 된다.
즉, B=b-A'b/A'A*A 가 된다.
C는 그럼, 이 작업을 B와 A에 대해 두번 해주면 얻을 수 있다. A에 있던 모든 column에 대해 이 변환을 하고 나면 orthognal column들만 있는 matrix를 얻을 수 있고, 길이로 나눠주면 orthonomal하게까지 만들 수 있다.
이걸 A=QR처럼 만들 수도 있다고 한다. 이때 R는 upper triangle 꼴이라고.
Determinant
det(A) = |A| 로 표기한다. A가 square일 때, det(a) 가 0이 아니면 역행렬이 존재한다.
det의 10가지 특성은 아래와 같다.
1. det(I) =1
2. row를 한번 바꾸면 det의 sign 이 바뀐다.
3-1. 한 row에 t를 곱하면 기존 det에 t를 곱한 값이 된다.
3-b. 다음이 성립한다.
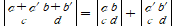
4. row둘이 같으면 det=0이다.(2번에 의해 교환시 부호 반대. 근데 값이 같으므로 0)
5. row 끼리의 선형결합시에는 det이 불변한다.
6. row중에 0인 row가 잇다면 3-b에 의해 det=0
7. det(A) = det(U) U: elimination결과
8. A가 singular 면 det(A)=0
9. det(AB) = det(A) det(B)
det(2A) 2^n*det(A)
10. det(A')=det(A)
det 공식 만드는 방법은 Cofactor를 이용.
det A=a11c11+a12c12....+a1nc1n
Cofactor matrix가 있을 때, A^(-1)= C'/|A| 근데 이걸 구하는건 너무 어려워서 나온 것이 Cramer's rule
Ax=b 에서, xhat는 A^(-1)b. 이때,
x1=1/det(A)*det(B1) (Bj는 A의 j번째 column을 b로 교체한 것) 이라는 것.
역행렬에 비해 determinant를 구하는 것은 elimation을 이용해 diagnal를 보면 훨씬 쉽다.
참고로 여기에 더해 3*3 짜리 행렬에서 det가 갖는 의미는, box의 부피이다.(Volume)
eigenvalue, eigenvector
어떤 단일 값 y(보통 람다 사용)가 있어서, Ax=yx를 만족한다고 할 때, 이 y가 eigenvalue이며, x가 이 eigenvalue에 해당되는 eigenvector이다.
정의에서 쉽게 알 수 있지만 eigenvalue값이 0이면 eigenvector는 null space에 있는 vector들이 된다.(동시에 A가 singular라는 의미이기도 하다.)
Projection matrix P가 있다면(A(A'A)^(-1)A'), eigenvector는 plane에 있는 벡터 및 수직인 벡터들일 것이고, eigenvalue는 1 혹은 0이 될 것임을 알 수 있다. eigenvector가 1 혹은 0 만 된다는 것은 중요한 포인트라 나중에 또 쓰게 된다.
eigenvector의 특이한 성질은 eigenvector의 합이 대각선의 합, 즉 tr(A)라는 점이다. 따라서 하나를 안다면, 나머지를 빠르게 구할 수 있는 사례가 종종 있다.
eigenvalue들을 구하는 방법에는 두 가지가 있다.
1. (A-yI)x=0 을 solve하는 방법. 즉 elimination을 이용하는 방법
2. 일부 사례의 경우, trace와 singular의 성질을 이용해 빠르게 찾을 수 있는 방법.
예를 들어 permutaion matrix[0 1 // 1 0] 에서 eigenvalue를 구해보면, 1과 -1인것을 쉽게 구할 수 있다. 이때 합은 0이며, 이는 tr과 일치한다.
eigenvalue에 대해 주의해야 되는 점은 두 가지다. 첫째로, 실수 행렬에 대해서 허수 eigenvalue가 있을 수 있다. 또한, eigenvalue가 중복되는 경우, eigenvector가 부족할 수도 있다. 항상 부족한 것은 아닌데, 대표적인 예로 I를 생각하면 전부 1이지만 eigenvector는 n개 존재하는 경우도 있다.
A에 대해, eigenvector들을 모두 모아 놓은 S라는 matrix가 있고, 이게 n*n(즉 역행렬이 존재)이면, 이때 A는 diagonalizable하다.
따라서 A의 eigenvalue가 모두 다르거나, 같더라도 서로 다른 eigenvector가 있을 때 diagonalizable하다.
AS=SD (D: diagonal eigenvalue matrix)
이는 A의 n승이 필요한 문제에서 사용하게 된다. 또한 이 방법으로 A^2의 eigenvalue가 A와 같다는 것또한 쉽게 확인 가능하다.
특히 u_(k+1)=Au_k가 성립하는 관계에서 유용하게 쓰이는 특징이다. 특히 u_0를 eigenvector들의 선형 결합으로(rank가 n이므로 반드시 조합이 있다.) 표현하고 나면, 다음의 식이 성립한다.
A^k=SD^kS^(-1)이 되므로,
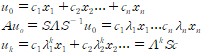
피보나치가 굉장히 유명한 예이다. Xk=[a_k a(k-1)]' 으로 두고 관계식을 세우면 위와 같은 풀이를 쉽게 만들 수 있다.
differential equation도 이와 비슷한 방식이다. 다른점은 exp^(yt) 꼴이 된다는 점. 해가 Sexp(Dt)S^(-1) 형태가 된다.(exp(Dt)는 행렬의 exp이다.)
Marcov matrix
Marcov matrix는 각열의 합이 1이면서, 각 entry가 0이상인 행렬이다. 열 하나씩에 확률 분포 하나라 생각하면 대충 맞다. 중요한 특징이 몇 가지 있는데,
- A의 power또한 여전히 특징을 보존한다.
- eigenvalue중에 하나가 반드시 1이다.
- 나머지 eigenvalue들의 절대값이 모두 1보다 작다.
Marcov matrix는 두 지역에서의 인구이동 같은 문제(인구의 총량이 보존되는 문제)를 푸는데 사용된다. 특히 오랜시간이 지났을 때의 상태는 eigenvalue가 1인 것 외의 나머지는 0으로 사라지므로, 매우 편하게 답을 구할 수 있다.
Symmetric Matrix
real symmetric matrix가 갖는 중요한 특징은, eigenvalue가 언제나 n개 있으며, 모두 실수라는 것이다. 즉, 언제나 orthonormal matrix Q가 존재한다. 따라서 A=QDQ'로 언제나 분해할 수 있다.
QDQ'를 요소별로 분해해 보면 꽤 재밌는 성질을 볼 수 있다.
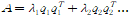
q'q는 길이인 반면 qq'는 행렬이다. 더 나아가, projection matrix(분모가 1이므로)이다. 즉, 모든 symmetric matrix는 combination of projection matrix가 된다!
또 하나 독특한 성질은, real symmetric matrix의 경우 elimination으로 pivot을 구하고 난 뒤에 부호를 확인하면, 이 부호의 개수(즉 양수 몇개, 음수 몇개)가 eigenvalue의 부호의 개수와 일치한다고 한다. 이러면 직접적인 값을 구하지 못하더라도 I를 더하고 뺌으로써 특정 범위내에 값이 몇개 존재하는지는 빠르게 셀 수 있게 된다.(부호가 바뀌는 것들 개수)
Positive Definite Matrix
Postivie Deifinite Matrix는 real symmetric matrix이면서, 다음의 특징들을 모두 만족하는 matrix이다.
1. 모든 eigenvalue들이 양수다. = 모든 pivot이 양수다. => det이 양수
2. 모든 subdeterminant 도 양수다.
또한 매우 중요한 특징이 있다.
3. 모든 벡터 x(원점 제외)에 대해, x'Ax>0을 만족한다!
그래서 그림을 그려보면, convex한 모양의 그림을 얻게 된다. saddle point가 없다. posdef를 사용하는 시점은, 그 점이 minima인지를 판단할 때이다. minima가 될 조건은 우선 1차 미분들이 전부 0이어야 한다. 하지만 이 특징은 saddle point에서도 동일하다. 차이점은, 2차 미분 행렬이 posdef라는 점이다. posdef이어야 minima인 점이 된다.
근데, positive definite가 만들어지는 아주 단순한 방법이 있다. 그게 바로 A'A. A가 rectangular여도, full column rank를 가졌다면, A'A 는 positive definite가 된다.
A가 pos def면 A^(-1) 또한 pos def이다. 또한, A와 B가 pos def라면 A+B도 pos def이다.
Similar Matrix
Similar Matrix라는 분류가 존재한다. (둘다 Square) 어떤 A와 B가 similar matrix라면, 다음의 관계가 성립한다.
B=M^(-1)AM 이 성립하는 M이 존재한다. 어디서 많이 본 형탠데, A와 D(diagonized matrix)가 이런 관계이다.
A와 B, B와 C가 similar 하다면, A와 C도 similar한 관계가 성립한다.
similar 한 matrix끼리는 같은 eigenvalue를 갖는다. 단 eigenvector는 변한다.
그렇다면 eigenvalue가 서로 같으면 similar한가? 그렇지는 않다. Jordan block도 같아야 similar하다. Jordan form은 깊이 다루지 않았다. 아주 정확하게 숫자들이 정해져 있는 조합에 대해서만 성립하며, 계산하기도 쉽지 않다.
SVD(Singular Value Decomposition)
개인적으로 생각하는, 선형대수학에 있어 가장 중요한 응용이 아닐까 싶은 부분. 모든 종류의 A를 다음으로 분해할 수 있다는 것이다.
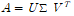
여기서 U와 V는 orthogonal matrix이며, 시그마는 diagnonal matrix이다. A가 pos def인 경우 편하게 U=V=Q가 되는 것과 비슷하다. U,V를 orthonormal라고 하면, 식을 조금 변형하면
AV=UD의 형태가 된다. 이를 보면, orthogonal row basis를 orthogonal column basis로 변환시키는 작업으로도 볼 수 있는 것이다.
그럼 이 U와 V를 어떻게 구하느냐.
AA'를 보면, AA'=UDV'VD'U'=UDD'U'=UYU' (Y는 제곱 값들이 들어 있다.) 즉, U는 AA'의 eigenvector들이 되는 것이다.
V도 이와 같은데, A'A의 eigenvector가 된다. 단 주의점은, 부호를 어떻게 할당할까를 사전에 아는 방법은 없다. 따라서 대입해서 부호를 확인해 맞춰줘야 한다.
Change of basis
압축의 원리는 basis을 바꿔 주는 것이다. 예를 들어[1,-1,1,-1,1,-1]이 있다면, 만약 standard basis를 이용하면 계수가 모두 1 혹은 -1로, 이 정보를 전부 저장해야 할 것이다. 하지만, [1,-1,1,-1,1,-1] 에 해당하는 basis가 있다면? 이 것만 계수가 1이고 나머지는 0이 되어 저장할 필요가 없을 것이다. 계수가 0이 아니라 특정 기준치 이하라면 마찬가지로 무시해 줘도 사용자는 이를 알지 못할 것이다. 이 '어떤 basis를 쓰느냐?' 라는 게 제일 중요한 문제가 된다. 모든 분야에서 그야말로 제일 중요한 문제. basis이 가져야 될 요건 중에 inverse를 구하는게 빠르다는 것또한 중요,
자주 쓰이는게 퓨리에 basis, 웨이블릿 등.
Left inverse, Right inverse
full col rank 때 left inverse가, full row rank때 right inverse가 있다.
만드는 방법은,
[(A'A)^(-1)A']A=I
A[A'(AA')^(-1)]=I 처럼 만들 수 있다.
left right를 뒤집으면? 결과물을 보면, ()를 다르게 묶음으로써 그것이 projection에 해당되는 것을 확인할 수 있다. 이론적으로 매우 적절한 결과인 셈!
pseudo inverse는 A^(+) 로 표기하며, VD^(+)U' 로 만든다. null 부분을 무시하고 invertible한 부분만 역행렬을 구하는 것
