8. Applications of Graph Neural Networks

작성자 : 장아연
0. Recap
Deep Graph Encoder
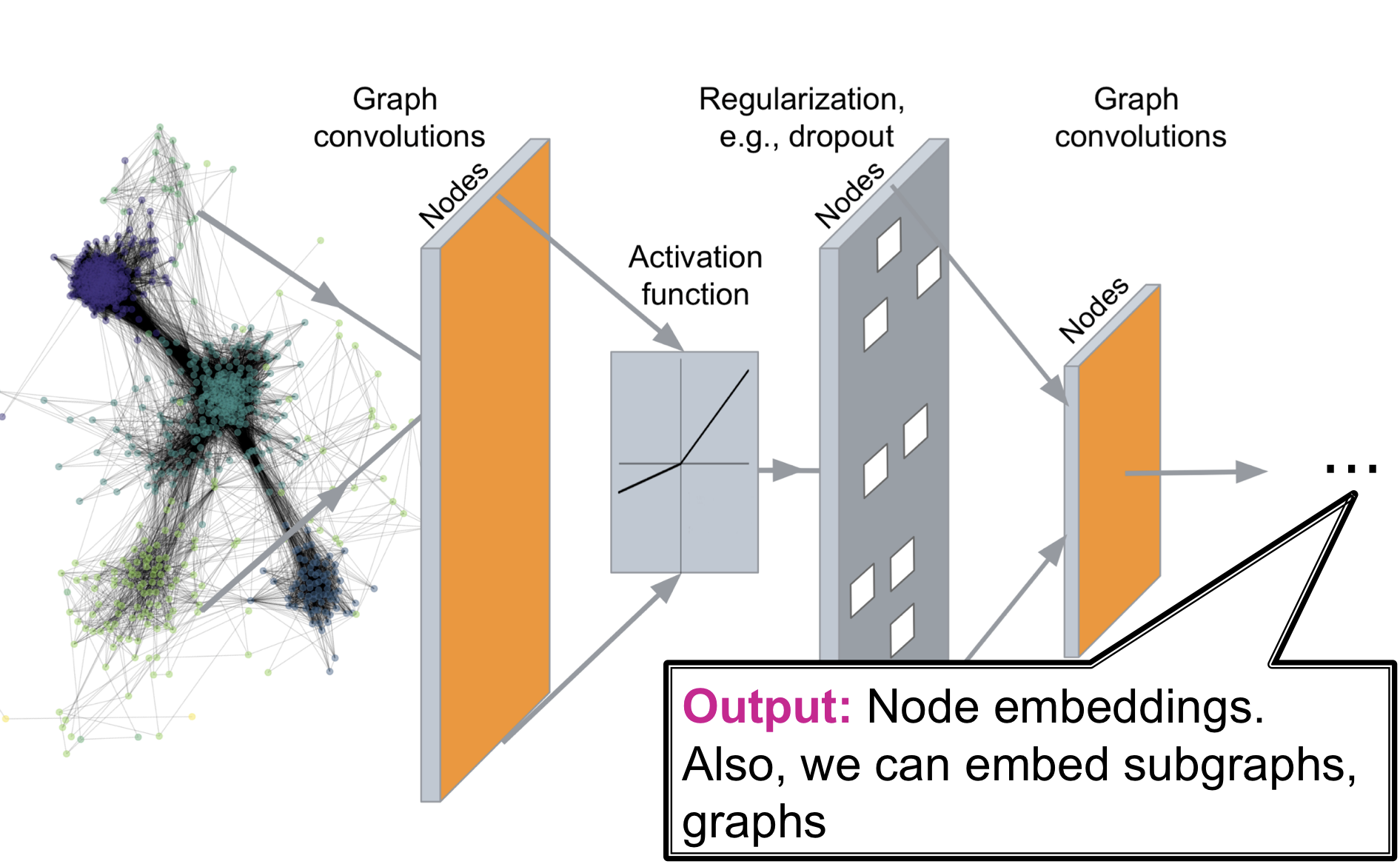
Deep Graph Encoders는 임의의 graph를 Deep Neural Network를 통과 시켜 embedding space로 사상 시키는 것
A General GNN Framework
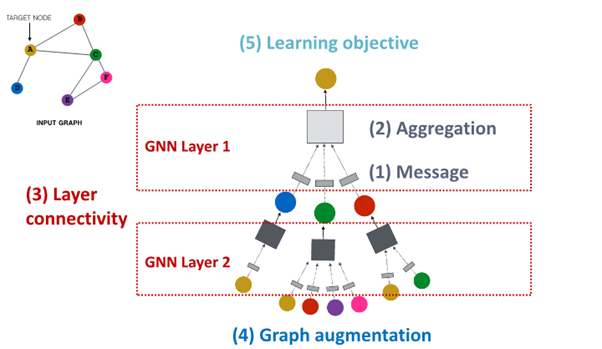
(4) Graph augmentation
: what kind of graph and feature augumentation can we create to shape the structure of this neural network
(5) Learning Objective
: learn objectives and how to make training work
1. Graph Augmentation for GNNs
Why Graph Augment
가정 : Raw input Graph 와 computational Graph는 동일
- Feature : lack features
- Graph Structure :
sparse -> inefficient passing
dense -> too costly passing
large -> not computational graph into GPU
즉, input graph는 embedding을 위한 computation graph의 적합한 상태가 아님.
Idea : Raw input Graph 와 computational Graph는 동일 X
Graph Augmentation Approaches
Graph Feature Augmentation
- lack features : feature augmentation을 통해 feature 생성
Standard Approach
필요성 : adj. matrix만 가지고 있는 경우 Input Graph에서 node feature가 없는 경우 흔히 발생
1. Constant Node Feature
Assign constant values to nodes
basically all the node have same future value of 1
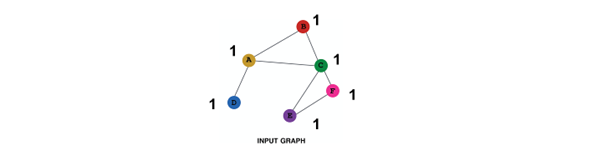
2. One-hot node feature
Assign unique IDs to nodes
IDs are converted to one-hot vectors
flag value 1 at ID of that single node

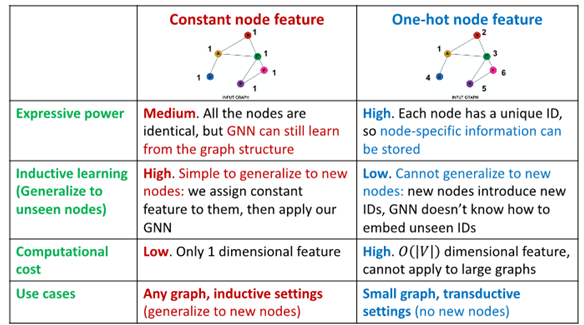
Constant Node Feature vs One-hot node feature
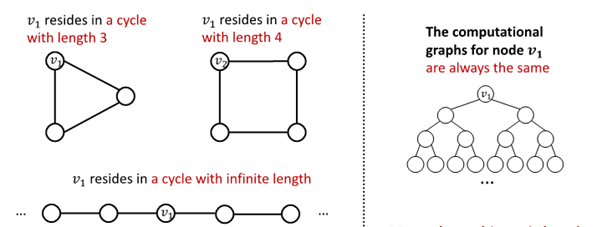
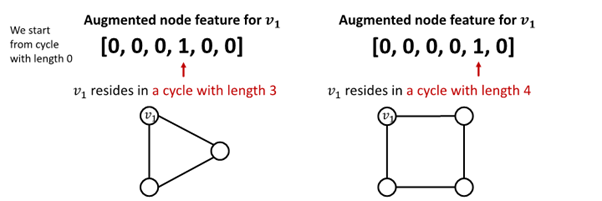
Cycle Count
필요성 : GNN 학습에 어려움을 겪는 특정 구조 존재
-
GNN은 이 속한 cycle의 길이 학습 불가
-
가 어떤 graph에 속해 있는지 구별 불가능
-
모든 node의 차수가 2임
-
computational graph는 같은 binary tree임
-
그 외 Node Degree, Clustering coeffiecient, PageRank, Centrality 등 이용
Graph Structure Augmentation
- too sparse : virtual node / edges를 생성
- too dense : message passing 과정에서 neighbors sampling
- too large : embedding 계산을 위해 subgraph sampling
Add Virtual Edge
개념
- virtual edge를 이용해 2-hop 관계의 이웃 노드 연결
- adj.matrix 대신 이용
예시
- Author(A)와 Author(B) 연결
: Author(A) -> paper -> Author(B)

Add Virtual node
개념
- virtual node를 이용해 graph의 모든 node를 연결
- 모든 node와 node는 distance 2를 가짐
: node(A) ->virtual node-> node(B)
예시
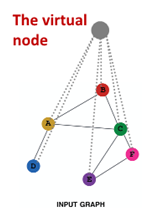
결과 : virtual node/edge 추가해 sparse한 graph에서 message passing 향상
Node Neighborhood Sampling
기존
- 모든 node는 message passing에 사용됨
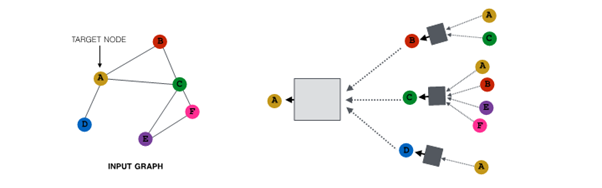
개념
- node neighborhood를 random sampling해 message passing 진행
예시 :
1. random하게 2개의 neighbor 선택해 sampling
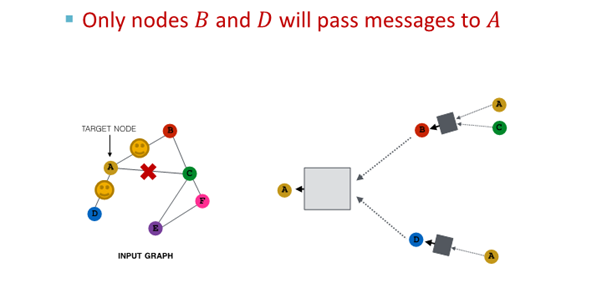
2. 다음 layer에서 다른 neighbor 선택해 resampling해 embedding 진행
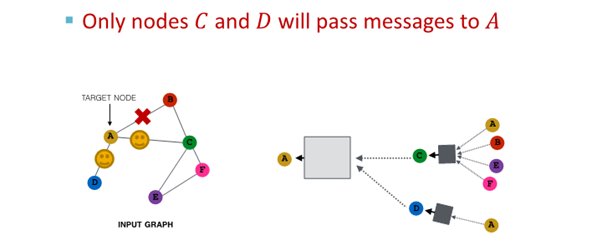
결과
- 모든 neighbor 사용한 경우와 유사한 embedding
- computational cost 경감
(large graph scaling 해줌)
2. Prediction with GNNs
Prediction head : How to train GNN?
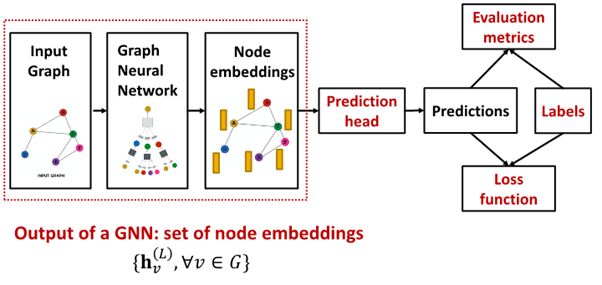
- : node L from graph neural network의 final layer
- Prediction head: final model's output
- Label : where label come from?
- Loss function : define loss function, what to optimize
Different Prediction Head
서로 다른 prediction head에 따라 서로 다른 task가 요구됨
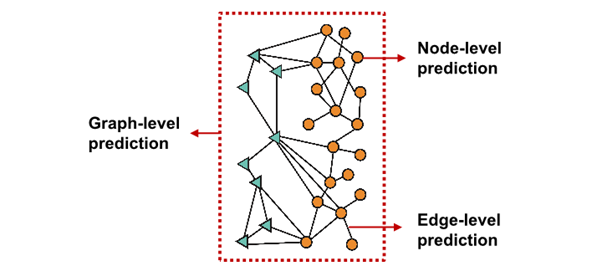
Node-level task
- node embedding 사용해 예측
- prediction head : { }
get -dim node embedding from GNN computation - way prediction의 경우
classification : classify among categories
regression : regress on target - ==
output head of given node=matrix time final embedding of node - : map node embedding from (embedding space) to (prediction)
Edge-level task
- node embedding pair 사용해 예측
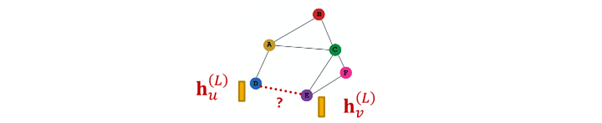
- -way prediction의 경우 : =
option for edge level prediction
1. Concatenation + Linear transformation

- =
- : 2d-dimensional => -dim embedding
2. Dot product
- =
- only applied to 1 way prediction (binary prediction)
- for -way prediction : multi-head attention과 유사
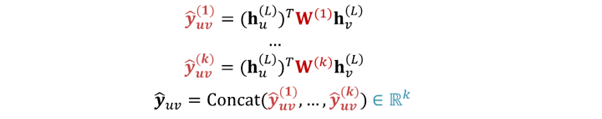
- trainable different matrix : ... 이용
=> every class get to learn its own transformation - prediction for every class인 ... 를 concat해 final prediction인 구함
Graph-level task
- graph 속 모든 node embedding 이용해 예측
- ={ }
take individual node embedding for every node and aggregate them to find embedding in graph
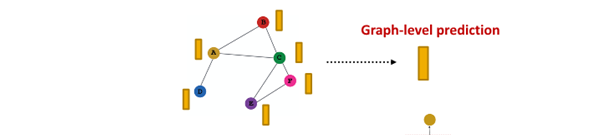
- 과 GNN에서 유사
option for Graph level prediction
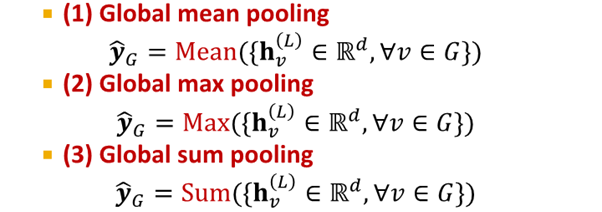
위 3개는 small graph에 적합함
large graph를 global pooling하여 information lose

- solution :
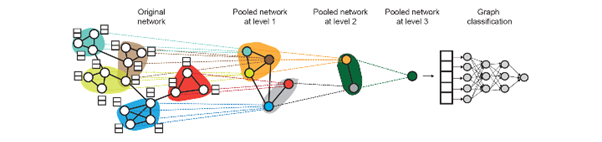
Hierarchical Global Pooling
Hierarchical Global Pooling
- 모든 node embedding을 위계 따라 aggregate
개념 예시

DiffPool idea : Hierarchically pool node embedding
3. Training Graph Neural Network
Prediction & labels : ground truth come from
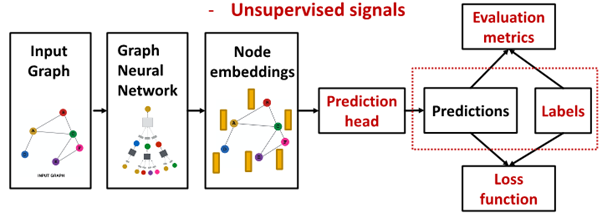
Supervised Label vs Unsupervised Signal
1. supervised learning
- label from external source
node label : citation network (node가 소속된 학문 분야)
edge label : transition network (edge의 fraudulent 여부)
graph label : among molecular graph, drug likeness graph
- unsupervised learning
- only graph, no external label
- find supervision signal in graph
node label : Node statistics : clustering coefficient , Pagerank
edge label : Link Prediction : hide edge between node and predict it
graph label :Graph statistics : predict each graph are isomorphic
Loss function : compute final loss
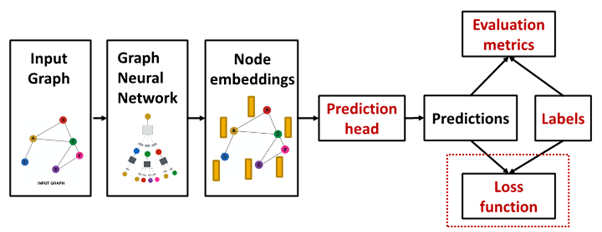
Setting for GNN training
- data point (node / edge / graph)
- : prediction at all level for label

GNN은 Classification과 Regression 모두 사용 가능 그러나 각각 loss function과 evaluation이 다름
Classification Loss
- Classification : 예측값 의 discrete value
- Node classification : node가 속한 카테고리 예측
Cross entropy (CE)
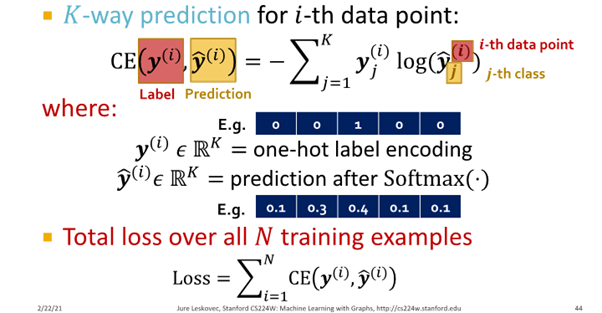
Regression Loss
- Regression : 예측값 의 continuous value
- mocular graph의 drug 유사도 예측
Mean Squared Error (MSE) : L2 loss

Evaluation metric : measure success of GNN
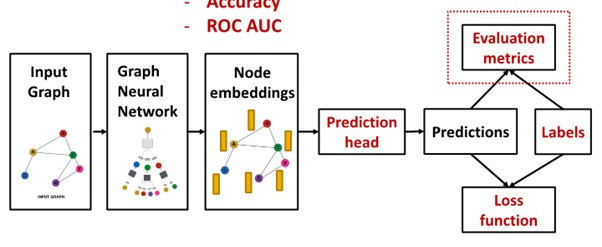
Evaluate Regression

Evaluate Classification
- multi-class classification : Accuracy
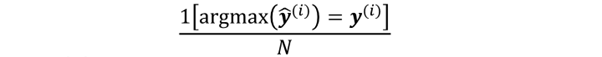
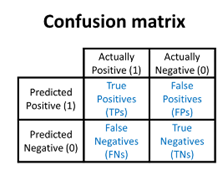
- binary classification : Confusion matrix, ROC Curve
- Accuracy : =
- Precision :
- Recall :
- f1-score :
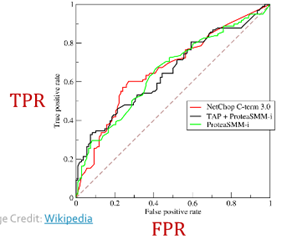
- TPR = recall =
- FPR =
- dashed line : random classifier의 performance
- threshold : binary classifier에 따라 값 다름
- ROC AUC : ROC curve 밑에 면적
4. Setting - up GNN Prediction Tasks
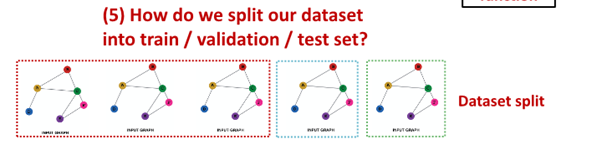
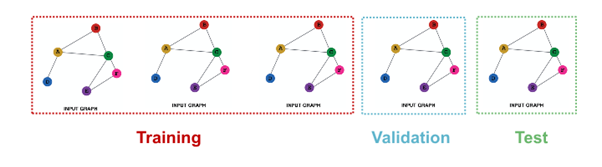
Fixed split vs Random split
Fixed split
- Train : GNN parameters를 optimize에 사용
- Validation : model/hyperparameters를 develope
- Test : final performance를 report하는 데 사용
-> test 결과에 대한 해당 실행 결과 보장X
Random split - randomly split training / validation / test dataset
-> 서로 다른 random seed에 대해 performance를 average함
Why Splitting Graph is special
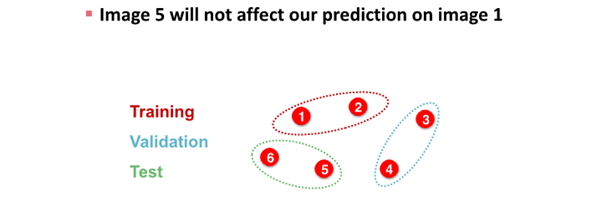
image data splite하는 경우
- image classification은 모든 data point가 image로 각각의 data가 서로 independent함
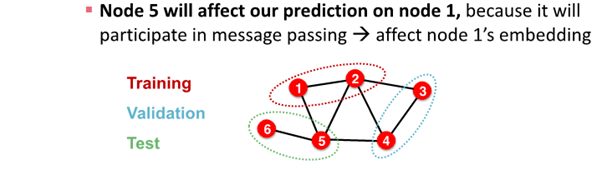
graph data splite하는 경우
- node classification은 모든 data point가 node로 각각의 data가 서로 dependent함
- node 1과 node 2는 node 5를 예측하는데 영향을 줌
: node 1과 node2가 train data, node 5가 test data인 경우, information leakage 발생 가능
solution
1. Transductive setting
- entire graph in all dataset
- only split label
- dataset consist of one graph
- node / edge prediction
- train : entire graph, use node 1 & 2 label
- validation : entire graph, use node 3 & 4 label

2. Inductive setting
- different graph in each dataset
- dataset consist of multiple graph
- generalize to unseen graph
- node / edge / graph task
- train : embedding 계산 graph over node 1 & 2, train use node 1 & 2 label
- validation : embedding 계산 graph over node 3 & 4, evaluate node 3 & 4 label

Example
1. Node Classification
- transductive node classification :
can observe entire graph but only observe respective nodes

- inductive node classification :
each contain independent graph

- Graph Classification
- only in inductive setting
- test on unseen graph
- Link Classification
- predict missing edge
- unsupervised / self-supervised task
-> create label & dataset split
= we hide edge & let GNN predict whether edge exist

Setting up Link Prediction
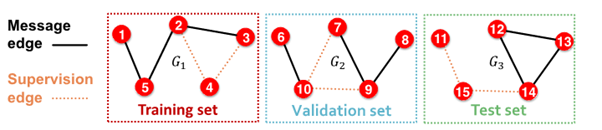
1-0. Assign edge as Message edges or Supervision edges
- Message edges : GNN message passing에 사용
- Supervision edges : objectives 계산에 사용
1-1.
message edges : remain in graph
supervision edges : supervise edge prediction made by model
2-0. split edges as train / validation / test
2-1. Inductive link prediction split의 경우
- contain independent graph in dataset
- 각 dataset에는
message edges와supervision edges가 포함됨 supervision edgesnot fed in GNN
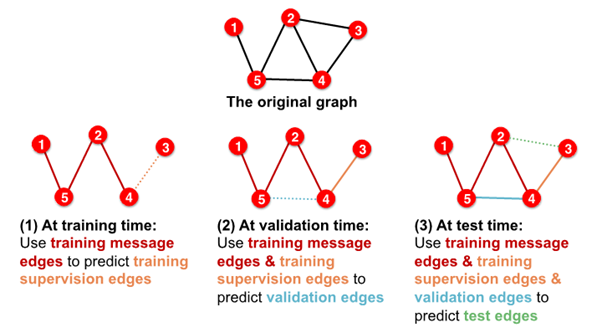
2-2. Transductive link prediction split의 경우
- after train,
supervision edgesknown to GNN - use
supervision edgesat validation time
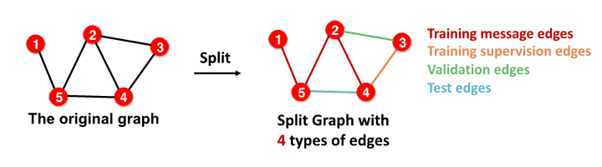
- in sum, 4 types of edges
3개의 댓글
[15기 이성범]
Graph에서 Feature를 Augmentation하는 방법으로는 단순히 모든 노드에 1을 추가하는 Constant Node Feature 방법과
노드의 ID를 원핫벡터 형식으로 나타내는 One-hot node feature 방법과 그래프의 cycle의 길이를 파악하는 Cycle Count 방법과
Node Degree, Clustering coeffiecient, PageRank, Centrality 등의 방법이 존재한다.
Graph의 Structure를 Augmentation하는 방법으로는 가상의 edge를 사용해 2-hop 관계의 이웃 노드 연결하는 Add Virtual Edge 방법과
가상의 node를 이용해 graph의 모든 node를 연결하는 Add Virtual node 방법과 node neighborhood를 random sampling하는 Node Neighborhood Sampling 방법과
subgraph를 sampling하는 subgraph sampling 방법 등이 있다.
GNN에서도 CNN과 비슷하게 학습 과정에서 Concat, Dot product, pooling, CELoss, MSELoss 등을 사용한다.
GNN에서는 데이터를 splite할 때, graph data는 서로 종속관계이기 때문에 단순히 무작위로 짜르게 된다면 정보 손실이 발샐하게 된다.
따라서 전체 그래프를 사용할 때는 라벨을 기준으로 train과 validation을 구분하는 Transductive setting 방법을 사용하고,
각기 다른 그래프를 사용할 때는 각기 다른 그래프를 각각 train과 validation으로 나눠 각각의 embedding을 계산하여 각각의 label을 맞추는 방식인 Inductive setting 방법을 사용한다.
Graph Augmentation
- 필요한 이유 : raw input graph는 임베딩을 위한 computation graph의 효율적 상태가 아님
- Graph Feature Augmentation
- Constant Node feature : 모두 1
- One-hot node feature : ID 할당하고 ID를 원핫벡터로
- cycle count : GNN 학습에 어려움 겪는 특정 구조를 위함
- Graph Structure Augmentation
- add virtual edge : 2-hop 간의 노드 연결 표현(edge)
- add virtual node : 그래프의 모든 노드를 연결 (가상의 상위노드 ? 느낌)
- Node neighborhood sampling : 이웃 노드를 랜덤샘플링
Prediction with GNNs
1. Different Prediction head
- node level task : node emb 사용해서 예측
- edge level task : node emb pair 사용해서 예측, concat + linear transform / Dot product 옵션
- graph level task : 그래프 속 모든 node emb 이용해서 예측
Setting up GNN Prediction Tasks
1. Fixed split : train - parameter optimize / val - hyperparam tune / test - final perf.
2. Random split : random seed 다르게 해서 평균
Why splitting Graph is so special
- 이미지 : 데이터 서로 독립 / 그래프 : 데이터 서로 독립 X
- solution : Transductive setting, Inductive setting


14기 김상현
GNN의 augmentation과 학습 방법에 대해 이해할 수 있었습니다.
유익한 강의 감사합니다:)