[프로그래머스] Lv3. 파괴되지 않은 건물- JavaScript

문제분류 : 코팅테스트 연습

난이도 : Level 3

출처 : 프로그래머스 - 파괴되지 않은 건물

문제

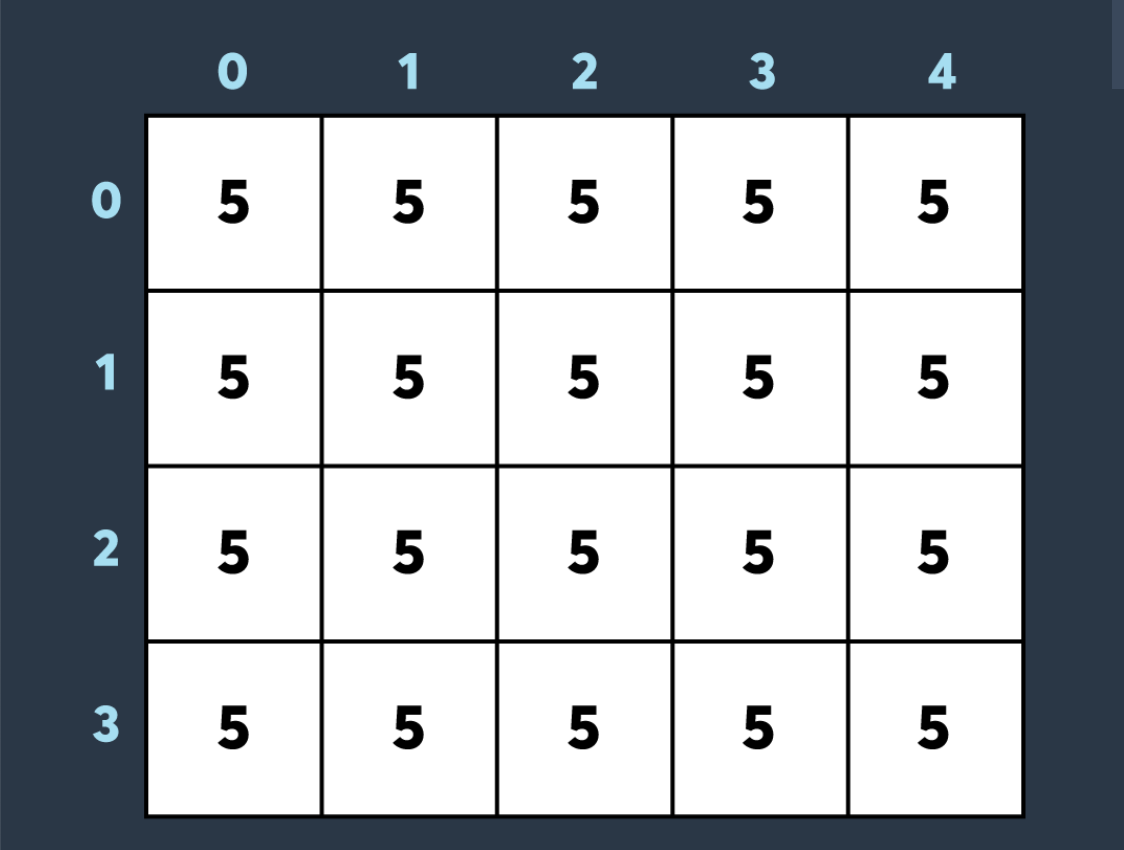
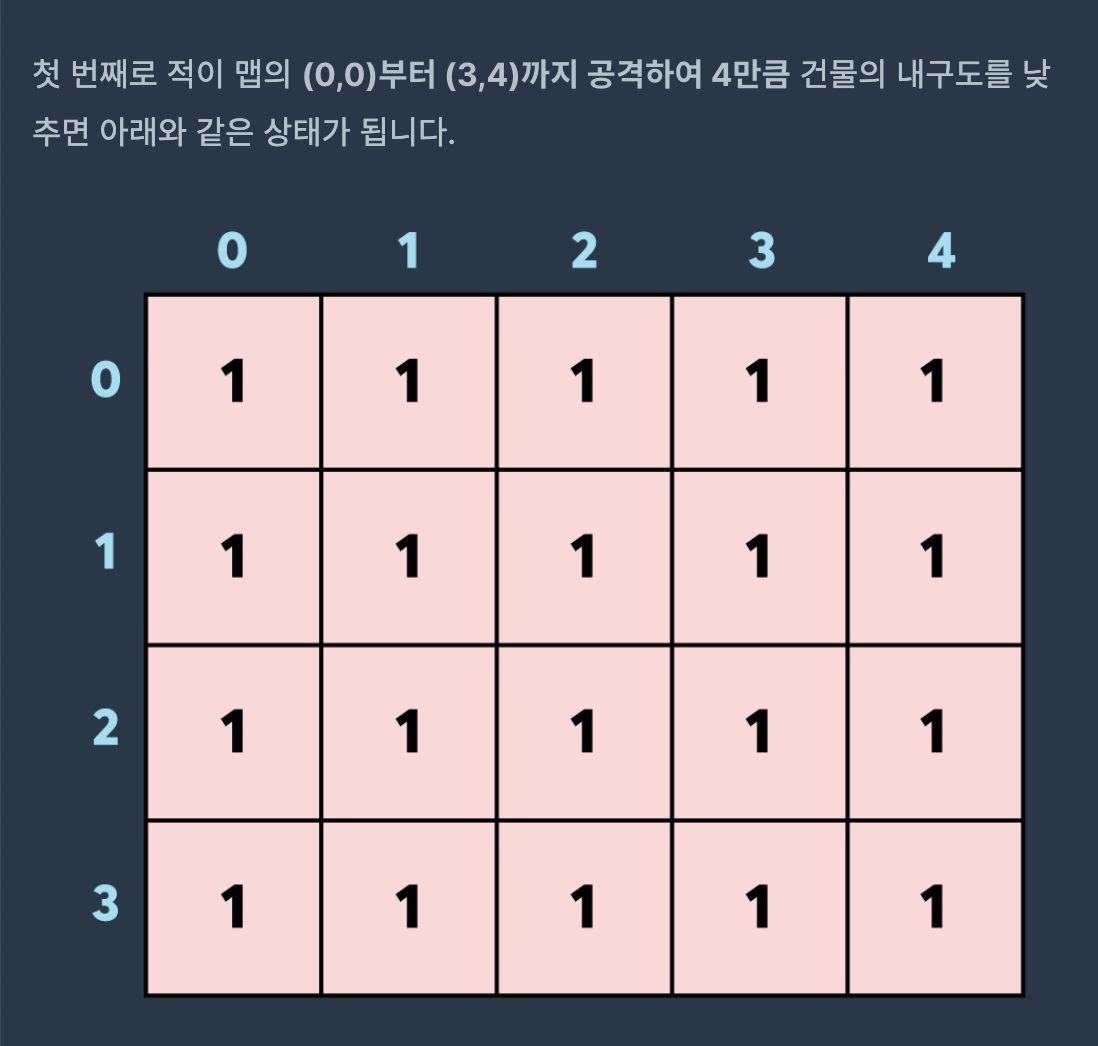
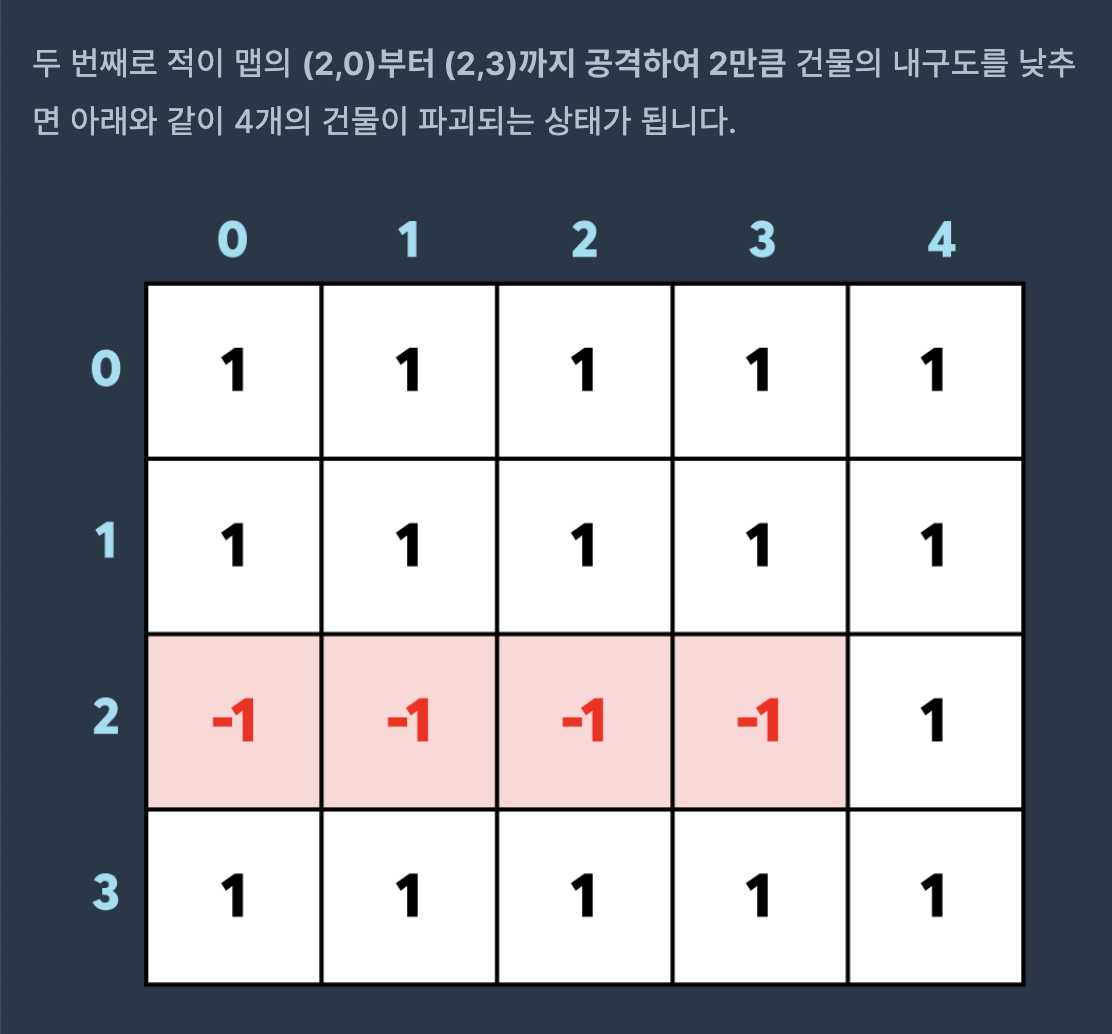
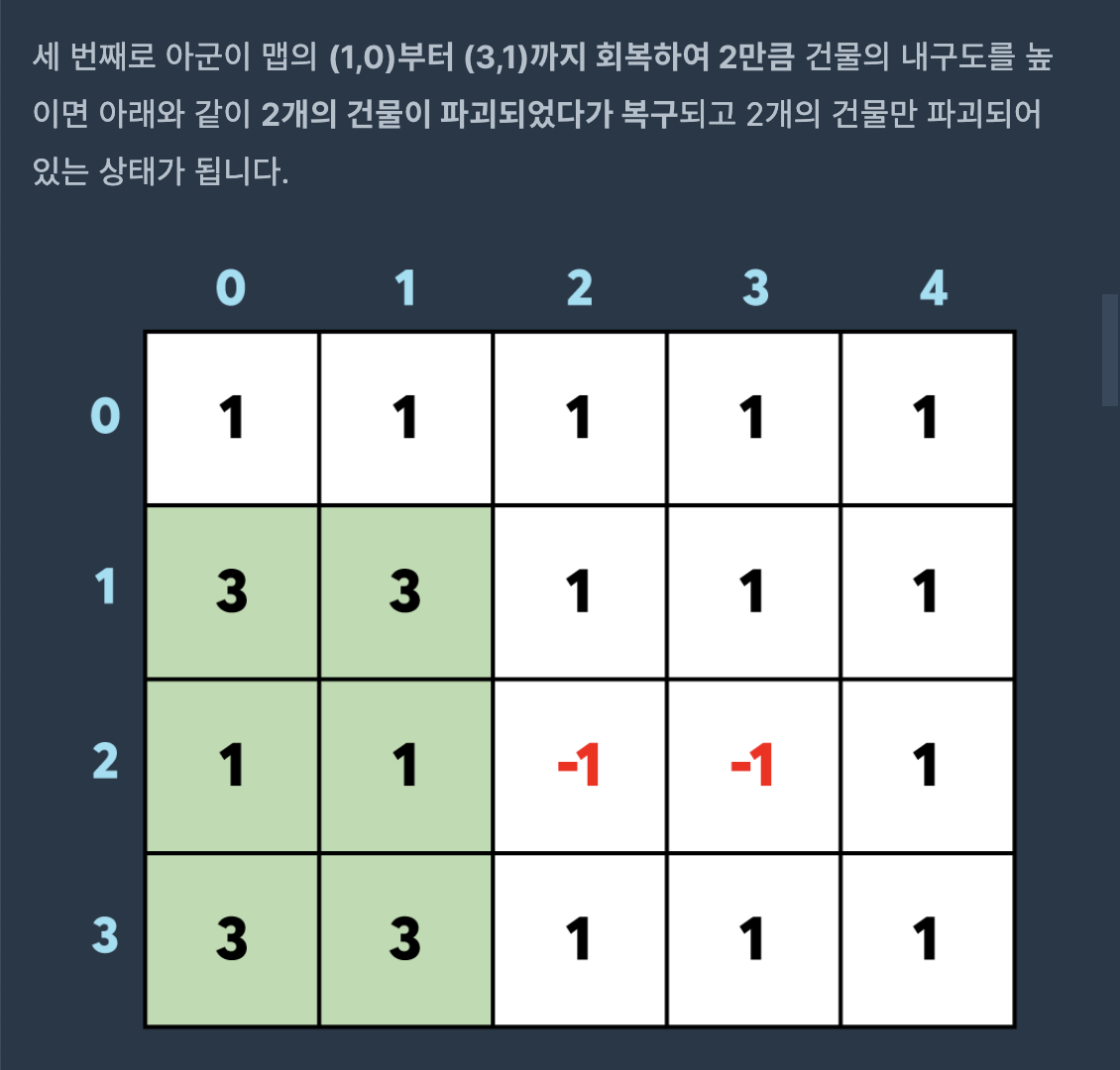
제한사항

📌 내가 생각한 풀이

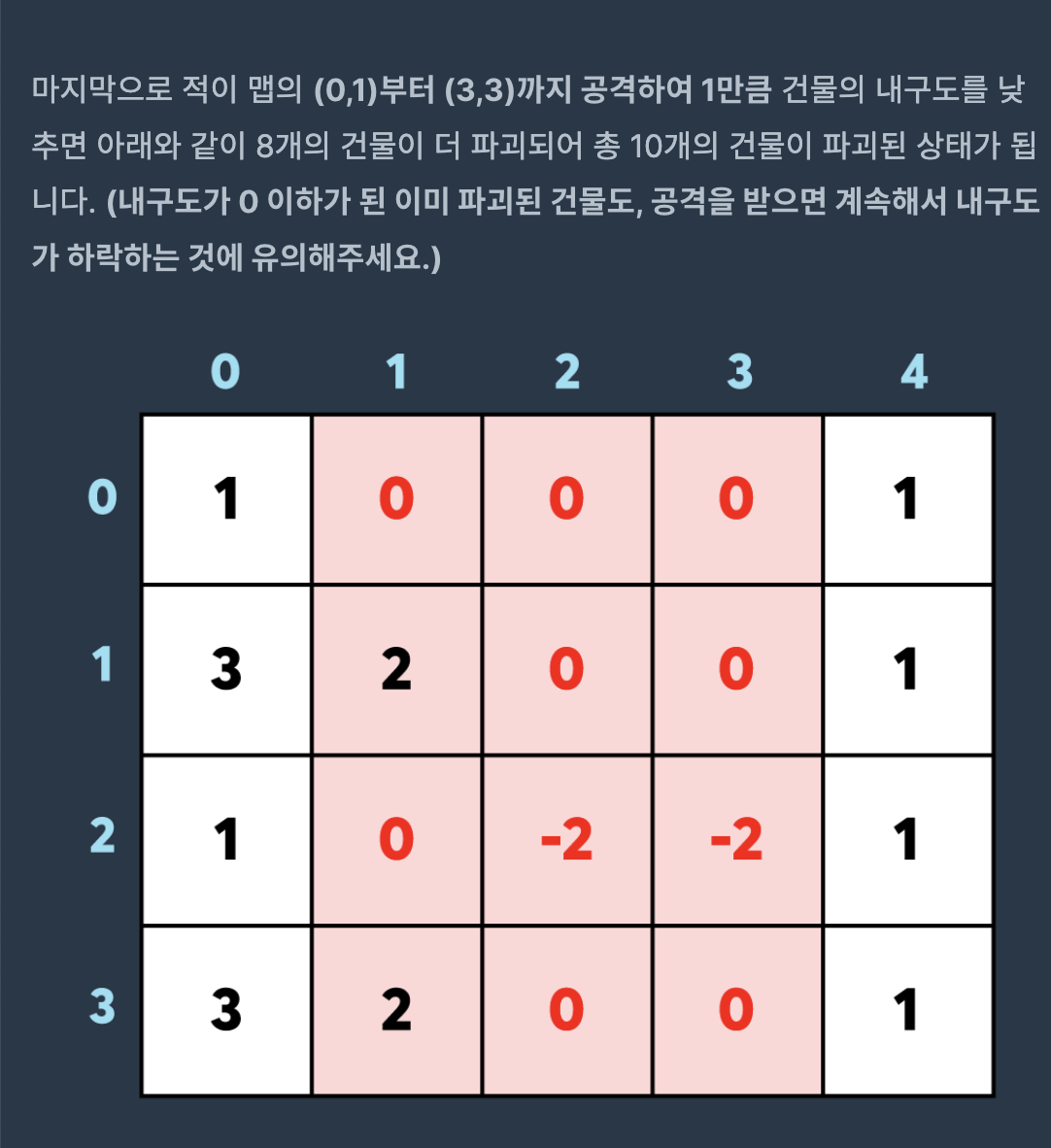
완전탐색으로 일일히 데미지를 주면 정확성 테케는 다 통과하지만, 시간복잡도 테케는 아무것도 통과하지못한다. 카카오 공식해설을 참고하여 누적합으로 풀자!

누적합풀이

예를들어 1차원 배열에서 0부터 3까지 -2의 데미지를 입힌다고 가정하자.
이를 누적합 데미지로 푼다면 [-2, 0, 0, 2]가 된다.
0부터 마지막 인덱스까지 값을 누적하면 [-2, -2, -2, 0]이므로 0부터 3까지 -2의 데미지를 입힌다는 것을 표현할 수 있다.
이것을 2차원으로 확장시키자. (0, 0)부터 (3, 3)까지 -2의 데미지를 입힌다고 하였을땐
[-2, 0, 0, 2]
[0, 0, 0, 0]
[0, 0, 0, 0]
[2, 0, 0, -2]
가 되고 이것을 행 누적따로, 열 누적따로 하면
[-2, -2, -2, 0]
[-2, -2, -2, 0]
[-2, -2, -2, 0]
[0, 0, 0, 0] 이 된다.
따라서 이 값을 board에 더하여 파괴되지 않은 건물을 구하면 된다.

function solution(board, skill) {
    var answer = 0;
    let wholeNum = board.length * board[0].length;
    let accArr = Array.from(Array(board.length+1), ()=>Array(board[0].length+1).fill(0));
    skill.forEach((data,idx)=>{
        let [type, r1, c1, r2, c2, degree] = data;
        switch(type){
            case 1:
                accArr[r1][c1] -= degree;
                accArr[r2+1][c2+1] -= degree;
                accArr[r1][c2+1] += degree;
                accArr[r2+1][c1] +=degree;
                break;
            case 2:
                accArr[r1][c1] += degree;
                accArr[r2+1][c2+1] += degree;
                accArr[r1][c2+1] -= degree;
                accArr[r2+1][c1] -=degree;
                break;
        }
        
    })
    for(var i =0; i<accArr.length; i++){
        for(var k = 0; k<accArr[i].length-1; k++){
            accArr[i][k+1] += accArr[i][k]
        }
    }
    for(var i =0; i<accArr[0].length; i++){
        for(var k = 0; k<accArr.length-1; k++){
            accArr[k+1][i] += accArr[k][i]
        }
    }
    board.forEach((d,i)=>{
        d.forEach((data,idx)=>{
            let sum = data + accArr[i][idx];
            sum > 0 ? answer++ : null
        })
    })
    return  answer;
}

📌 느낀점

누적합을 이용하여 각 요소에 특정 값을 더하거나 뺴는 방식을 처음 알게되었다. 브루트 포스를 이용하여 쓰는 것 보다 훨씬 시간복잡도 면에서 간단한 것 같아서 이 방식을 앞으로도 자주 애용해야겠다.